КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рівняння лінії
|
|
|
|
Найважливішим поняттям аналітичної геометрії є рівняння лінії.
Лінія – це геометрична множина точок, які мають певну властивість.
Наприклад, геометрична множина точок, рівновіддалених від двох заданих точок – це пряма (серединний перпендикуляр), а геометрична множина точок, рівновіддалених від однієї точки – це коло.
Рівняння лінії на площині – це рівняння  , яке за допомогою певного закону або правила
, яке за допомогою певного закону або правила 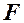 пов’язує змінні
пов’язує змінні 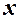 та
та 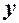 .
.
Основне означення аналітичної геометрії. Рівняння вигляду 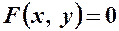 є рівнянням лінії
є рівнянням лінії 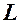 на площині
на площині 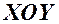 , якщо координати кожної точки, що належить лінії
, якщо координати кожної точки, що належить лінії 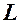 , задовольняють це рівняння, а координати кожної точки, яка не належить лінії
, задовольняють це рівняння, а координати кожної точки, яка не належить лінії 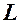 , не задовольняють рівняння
, не задовольняють рівняння 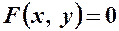 .
.
Виходячи з цього означення, виникають такі основні задачі аналітичної геометрії:
1. Дано рівняння деякої лінії. Треба за даним рівнянням знайти відповідний геометричний образ.
2. Дана лінія, як множина точок, які мають певну геометричну властивість. Треба скласти рівняння цієї лінії.
3. Задані рівняння двох ліній. Треба знайти точки перетину цих ліній або встановити, що задані лінії не перетинаються.
Приклад 1. Дано рівняння лінії 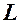 :
: 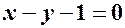 .
.
Очевидно, геометричним образом даного рівняння є множина точок прямої (рис. 1). Наприклад, 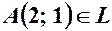 ; ;  ; ;
 ; ;
| . 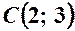 1
1 
1 2 Рис. 1 |
Приклад 2. Скласти рівняння кола радіуса 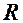 з центром у точці
з центром у точці 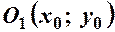 . Візьмемо довільну точку
. Візьмемо довільну точку  на колі. Як відомо, точки кола рівновіддалені від центра
на колі. Як відомо, точки кола рівновіддалені від центра 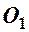 на відстань
на відстань 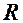 , тобто
, тобто  (рис. 2). За формулою відстані між двома точками:
(рис. 2). За формулою відстані між двома точками:
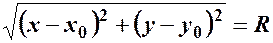 ,
або ,
або  – рівняння шуканого кола. – рівняння шуканого кола.
| 
  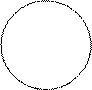 М(х; у) М(х; у)

 Рис. 2 Рис. 2
|
Приклад 3. Знайти точки перетину двох ліній:
а) 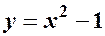 та
та 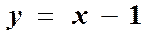 ; б)
; б)  та
та  .
.
Розв’язування. а) з основного означення аналітичної геометрії випливає, що координати точок перетину ліній повинні задовольняти систему рівнянь цих ліній:




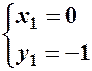
 .
.
Отже, маємо дві точки перетину 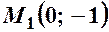 та
та 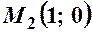 (рис. 3).
(рис. 3).
б) Пряма лінія  і коло
і коло  не мають спільних точок, оскільки система
не мають спільних точок, оскільки система 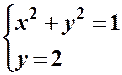

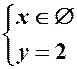 не має розв’язків (рис. 4).
не має розв’язків (рис. 4).
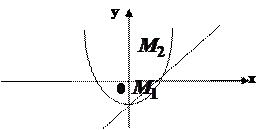 | |||
| |||
| Рис. 3 |
Рис. 4 |
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 2744; Нарушение авторских прав?; Мы поможем в написании вашей работы!