Основные определения. Лекция 10. Дифференциальные уравнения, основные понятия

Лекция 10. Дифференциальные уравнения, основные понятия

Дифференциальные уравнения. Ряды

Содержание лекции: Дифференциальные уравнения, основные понятия. Дифференциальные уравнения 1-го порядка. Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.

Цели лекции: знакомство с основными понятиями теории дифференциальных уравнений.

◙ Дифференциальным уравнением (Д.У.) называется уравнение, связывающее независимую переменную х, искомую функцию y = f (x) и ее производные y¢, y¢¢, …, y ^{( n )}: F (x, y, y¢, y¢¢, …, y ^{( n )}) = 0. (1)

Если это уравнение можно разрешить относительно п -ой производной, то его можно записать в виде y ^{( n )} = f (x, y, y¢, y¢¢, …, y ^{( n- 1)}). (1¢)

◙ Порядком Д.У. называется порядок наивысшей производной, входящей в уравнение.

◙ Д.У. (1) называется линейным, если левая часть его есть многочлен первой степени относительно y, y¢, y¢¢, …, y ^{( n )} (и не содержит их произведний), т.е. a ₀(x) y ^{( n )}+ a ₁(x) y ^{( n -1)}+…+ a_n (x) y = f (x), (2)

где a ₀(x), a ₁(x), …, a_n (x) – коэффициенты уравнения (определены и непрерывны в некотором интервале); f (x) – правая часть уравнения.

◙ Уравнение (2) называется однородным (без правой части), если f (x) = 0.

◙ Уравнение (2) называется неоднородным (с правой частью), если f (x) ¹ 0.

◙ Решением или интегралом Д.У. называется всякая функция y = j (x), которая, будучи подставлена в уравнение (1), превращает его в тождество.

Решить, или проинтегрировать, данное Д.У. означает найти все его решения в заданной области.

График решения называется интегральной кривой.

◙ Общим решением Д.У. (1) называется такое его решение:

у = j (х, С ₁, С ₂, …, С_п),

которое содержит столько независимых произвольных постоянных С ₁, С ₂, …, С_п , каков порядок этого уравнения.

Если общее решение задано в неявном виде Ф (х, у, С ₁, С ₂, …, С_п) = 0, то оно называется общим интегралом.

◙ Всякое решение Д.У., которое получается из общего решения, если приписать определенные значения произвольным постоянным, в него входящим, называется частным решением этого Д.У., у = j (х, С ₁, С ₂, …, С_п), и, соответственно, Ф (х, у, С ₁, С ₂, …, С_п) = 0, называется частным интегралом.

При заданных начальных условиях при х = х ₀: 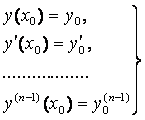(н.у.)

постоянные С ₁, С ₂, …, С_п можно подобрать так, что функция

у = j (х, С ₁, С ₂, …, С_п), являющаяся решением уравнения (1), будет удовлетворять этим условиям. Таким образом, введем новое понятие:

Задача Коши (начальная задача)

Найти решение y = j (x) Д.У. (1), удовлетворяющее начальному условию (н.у.).

Теорема 1. Если в уравнении y ^{( n )} = f (x, y, y¢, y¢¢, …, y ^{( n- 1)})

функция f (x, y, y¢, y¢¢, …, y ^{( n- 1)}) и ее частные производные по аргументам y, y¢, y¢¢, …, y ^{( n- 1)} непрерывны в некоторой области, содержащей значения

х = х ₀, y = у ₀, y¢ = у¢ ₀, ,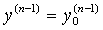

то существует и при том единственное решение y = j (x) задачи Коши.

Дата добавления: 2014-01-11