Лекция 11. Линейные дифференциальные уравнения высших порядков. Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами

Содержание лекции: Линейные дифференциальные уравнениявысших порядков (ЛДУ). Линейные однородные дифференциальные уравнения (ЛОДУ), структура их общего решения. ЛОДУ с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения (ЛНДУ), структура их общего решения. Метод вариации произвольных постоянных.

ЛНДУ с постоянными коэффициентами, метод подбора частного решения.

Цели лекции: знакомство с основными методами решения ЛОДУ и ЛНДУ.

Линейные дифференциальные уравнения высших порядков

◙ Д.У. п- го порядка называется линейным, если оно является многочленом первой степени относительно искомой функции y и ее производных y¢, y¢¢, …, y ^{( n )}, т.е. имеет вид:

a ₀(x) y ⁽ⁿ⁾ + a ₁(x) y ^{(n -1)} +…+ a_n (x) y = f (x), (1)

где a ₀(x), a ₁(x), …, a_n (x) и f (x) – заданные функции от х или постоянные, причем a ₀(x) ¹ 0 для всех значений х из той области, в которой рассматривается уравнение (1).

Функция f (x) называется правой частью уравнения.

В дальнейшем будем предполагать, что a ₀(x), a ₁(x), …, a_n (x) и f (x) – непрерывны при всех значениях х, причем a ₀(x)= 1.

Если f (x) º 0, то уравнение имеет вид

a ₀(x) y ⁽ⁿ⁾ + a ₁(x) y ^{(n -1)} +…+ a_n (x) y = 0 (2)

и называется линейным однородным (без правой части).

Если f (x) ¹ 0, то уравнение называется линейным неоднородным (с правой частью).

Рассмотрим некоторые свойства ЛОДУ, ограничиваясь уравнениями 2-го порядка.

Теорема 1. Если у ₁ и у ₂ – два частных решения ЛОДУ 2-го порядка

у¢¢ + а ₁ у¢ + а ₂ у = 0, (3)

то у ₁ + у ₂ – есть также решение этого уравнения.

Теорема 2. Если у ₁ есть решение ЛОДУ 2-го порядка (3) и С – постоянная, то Су ₁ есть также решение уравнения (3).

◙ Два решения уравнения (3) у ₁ и у ₂ называются линейно независимыми на отрезке [ a, b ], если

В противном случае решения называются линейно зависимыми,

т.е. $ l Î R: у ₁ = l у ₂.

◙ Если у ₁ и у ₂ – функции от х, то определитель

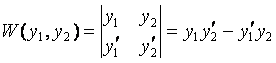
называется определителем Вронского (вронскианом) данных функций.

Теорема 3. Если функции у ₁ и у ₂ линейно зависимы на отрезке [ a, b ], то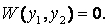

Теорема 4. Если определитель Вронского W (y ₁ , y ₂), составленный для решений y ₁ и y ₂ ЛОДУ(3), не равен нулю при каком-нибудь значении х = х ₀ на отрезке [ a, b ], где коэффициенты уравнения непрерывны, то он не обращается в нуль ни при каком значении х на этом отрезке.

Теорема 5. Если решения у ₁ и у ₂ уравнения (3) линейно независимы на отрезке [ a, b ], то ни в одной точке указанного отрезка.

Теорема 6. Если у ₁ и у ₂ – два линейно независимых решения уравнения (3), то у = С ₁ у ₁ + С ₂ у ₂, где С ₁ и С ₂ – произвольные постоянные, есть его общее решение.

Теорема 7. Каковы бы ни были н.у.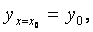

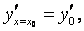
можно так подобрать значения С ₁, С ₂, чтобы соответствующее частное решение С ₁ у ₁ + С ₂ у ₂ удовлетворяло заданным н.у.

З а м е ч а н и е. Не существует общих методов для нахождения в конечном виде общего решения ЛДУ с переменными коэффициентами. Однако для уравнений с постоянными коэффициентами такой метод существует.

Дата добавления: 2014-01-11