ЛОДУ с постоянными коэффициентами

1. ЛОДУ 2-го порядка с постоянными коэффициентами имеет вид:

у¢¢ + pу¢ + qу = 0, p, q Î R (4)

Достаточно найти два линейно независимых частных решения.

Будем искать частные решения в виде:

y = e^kx, где k – const, (5)

тогда y¢ = ke^kx, y¢¢ = k²e^kx.

Подставляя эти выражения в (1), получим: e^kx (k² + pk + q) = 0.

Т.к. e^kx ≠ 0, то

k² + pk + q = 0. (6)

Следовательно, если k будет удовлетворять уравнению (6), то e^kx будет решением уравнения (4).

◙ Уравнение (6) называется характеристическим уравнением по отношению к уравнению (4).

Корни характеристического уравнения имеют вид:

, .

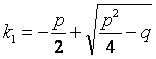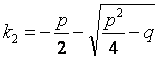Возможны случаи:

а) Если характеристическое уравнение имеет два различных действительных

корня, т.е. k ₁, k ₂ Î R (k ₁ ≠ k ₂ ), тогда общее решение имеет вид

.

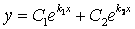б) Если характеристическое уравнение имеет два одинаковых действительных

корня, т.е. k ₁, k ₂ Î R (k ₁ = k ₂ ), тогда общее решение имеет вид

.

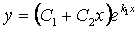в) Если характеристическое уравнение имеет два комплексных корня,

т.е. k ₁, k ₂ Î C: 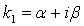, , 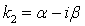где ,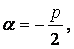

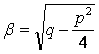тогда общее решение имеет вид .

2. ЛОДУ п -го порядка с постоянными коэффициентами имеет вид:

y ⁽ⁿ⁾ + a ₁ y ^{(n -1)} + … + a_ny = 0, (7)

где a ₁, …, a_n – постоянные.

Общее решение находится по следующему алгоритму:

1) составляем характеристическое уравнение;

2) находим его корни: k ₁, k ₂, …, k_п;

3) по характеру корней находим п линейно независимых частных решений;

4) строим общее решение.

З а м е ч а н и е. Трудность решения ЛОДУ с постоянными коэффициентами заключается в решении характеристического уравнения.

ЛНДУ 2-го порядка имеет вид:

у¢¢ + а ₁ у¢ + а ₂ у = f (x), (8)

где a ₁, a ₂ – заданные функции.

Теорема 8. Общее решение неоднородного уравнения (8) представляется как сумма какого-нибудь частного решения этого уравнения 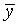и общего решения у ₀ соответствующего однородного уравнения

у¢¢ + а ₁ у¢ + а ₂ у = 0, (9)

т.е. общее решение неоднородного уравнения (8) имеет вид .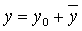

П р и м е ч а н и е. Общий метод нахождения частных решений неоднородного уравнения (метод вариации произвольных постоянных) рассмотреть самостоятельно. (См.[5],стр.88)

Рассмотрим лишь метод подбора частного решения для ЛНДУ с постоянными коэффициентами.

Сначала рассмотрим

Метод подбора частного решения по специальной правой части f (x) для линейного неоднородного уравнения 2-го порядка с постоянными коэффициентами:

у¢¢ + ру¢ + qу = f (x), p, q Î R.

1. Если правая часть имеет вид 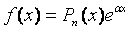, где P_n (x) – многочлен п- ой степени, то структура частного решения 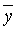зависит от того, является ли a корнем характеристического уравнения k ² + pk + q = 0 или нет. Поэтому возможны варианты:

а) если число a не является корнем характеристического уравнения, то частное решение ищется в следующем виде:

,

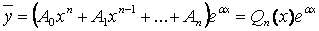где Q_n (x) – многочлен п- ой степени (такой же степени, что и P_n (x)) с

неопределенными коэффициентами, которые находятся после подстановки 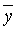, , 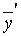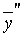в исходное уравнение;

б) если число a есть простой (однократный) корень характеристического уравнения, то ;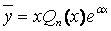

в) если число a есть двукратный корень характеристического уравнения, то .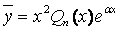

2. Если правая часть имеет вид 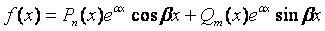, где P_п (x), Q_т (x) – многочлены п- ой и т- ой степени соответственно, то структура частного решения 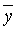зависит от того, являются ли a ± ib корнями характеристического уравнения k ² + pk + q = 0 или нет. Поэтому возможны варианты:

а) если числа a ± ib не являются корнями характеристического уравнения, то ,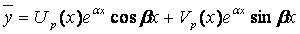

где U_p (x), V_p (x) – многочлены (с неопределенными коэффициентами), степень которых равна наивысшей степени многочленов P_n (x), Q_m (x), т.е. ;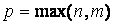

б) если числа a ± ib являются корнями характеристического уравнения, то ,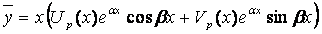

где U_p (x), V_p (x) – многочлены как в пункте а).

Частный случай: если f (x) = М cos bx + N sin bx,

где М, N – постоянные числа, то

а) если числа ± ib не являются корнями характеристического уравнения, то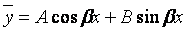

(где А и В – числа, подлежащие определению);

б) если числа ± ib являются корнями характеристического уравнения, то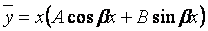

(где А и В – числа, подлежащие определению).

Метод подбора частного решения по специальной правой части f (x) для неоднородного линейного уравнения высшего порядка с постоянными коэффициентами

1. Если правая часть имеет вид f (x) = P_n (x) e^ax, где P_n (x) – многочлен п- ой степени, то различают два случая:

а) если число a не является корнем характеристического уравнения, то

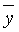= Q_n (x) e^ax ;

б) если число a есть корень кратности m характеристического уравнения, то 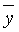= х^m Q_n (x) e^ax.

2. Если правая часть имеет вид f (x) = М cos bx + N sin bx, где М, N – постоянные числа, то различают два случая:

а) если число ib не является корнем характеристического уравнения, то

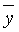= А cos bx + В sin bx;

б) если число ib есть корень характеристического уравнения кратности m, то 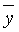= х^m [ А cos bx + В sin bx ].

3. Если правая часть имеет вид f (x) = P (x) e^ax cos bx + Q (x) e^ax sin bx,

где P (x), Q (x) – многочлены, то различают два случая:

а) если число a + ib не является корнем характеристического уравнения, то 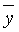= U (x) e^ax cos bx + V (x) e^ax sin bx,

U (x), V (x) – многочлены, степень которых равна наивысшей степени многочленов P (x), Q (x);

б) если число a + ib есть корень кратности m характеристического

уравнения, то 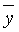= х^m [ U (x) e^ax cos bx + V (x) e^ax sin bx ].

3.3 Лекция 12. Числовые ряды. Функциональные ряды. Степенные ряды, ряды Тейлора.

Содержание лекции: Числовые ряды. Положительные ряды, признаки сходимости положительных рядов. Знакопеременные и знакочередующиеся ряды. Функциональные ряды, степенные ряды. Ряды Тейлора.

Цели лекции: знакомство с основными понятиями числовых и функциональных рядов, методами исследования рядов на сходимость, примерами разложения в степенные ряды некоторых элементарных функций.

1. Числовые ряды

◙ Выражение вида (1)

где и_п Î R (n = 1, 2, …) называется числовым рядом. Числа и ₁, и ₂, …, и_п, … называются членами ряда, число и_п – общим членом ряда.

◙ Сумма 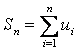называется частичной суммой ряда, а сумма

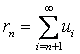называется п -ым остатком ряда.

◙ Если существует конечный предел 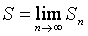, то его называют суммой ряда (1), а ряд (1) называется сходящимся. Если 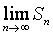не существует (в частности бесконечен), то ряд (1) называется расходящимся.

Теорема 1. (необходимый признак сходимости ряда).

Если ряд (1) сходится, то .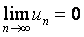

Обратное утверждение не верно.

Пример. Гармонический ряд 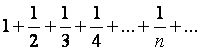расходится, хотя .

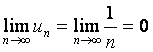Теорема 2. (достаточный признак расходимости ряда).

Если 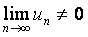, то ряд (1) расходится.

З а м е ч а н и е. Сходимость или расходимость числового ряда не нарушается, если в нем отбросить любое конечное число членов. Но его сумма, если она существует, при этом изменяется.

◙ Если все члены ряда и_п > 0, то данный ряд называется положительным рядом.

Дата добавления: 2014-01-11