Пример

Компания рассматривает целесообразность принятия проекта с денеж­ным потоком, приведенным в гр 2 табл 9.10. Цена капитала компании 12% Как правило, проекты со сроком погашения, превышающем 4 года, не прини­маются. Требуется сделать анализ с помощью критериев обыкновенного и дисконтированного сроков окупаемости.

Из приведенных в табл. 9.10 расчетов видно, что РР - 4 го­дам (при точном расчете РР = 3,5 года), a DPP = 5 годам (при точном расчете DPP = 4,9 года). Таким образом, если решение принимается на основе обыкновенного срока окупаемости, то проект приемлем, если используется критерий дисконтиро­ванного срока окупаемости, то проект скорее всего будет от­вергнут.

Показатель срока окупаемости инвестиции в инновацию очень прост в расчетах, вместе с тем он имеет ряд недостатков, которые необходимо учитывать при проведении анализа.

Во-первых, он не учитывает влияние доходов последних периодов. В качестве примера рассмотрим два проекта с оди-

наковыми капитальными затратами (13 млрд р.), но различны­ми прогнозируемыми годовыми доходами: по проекту А - 5,3 млрд р. в течение трех лет; по проекту Б - 4,8 млрд р. в течение десяти лет. Оба эти проекта в течение первых трех лет обеспе­чивают окупаемость капитальных вложений, поэтому с пози­ции данного критерия они равноправны. Однако очевидно, что проект Б гораздо более выгоден.

Во-вторых, поскольку этот метод основан на недисконти-рованных оценках, то он не делает различия между проектами с одинаковой суммой кумулятивных доходов, но различным распределением ее по годам. Так, с позиции этого критерия проект А с годовыми доходами 60, 80, 40 млрд р. и проект Б с годовыми доходами 40, 60, 80 млрд р. равноправны, хотя оче­видно, что первый проект более предпочтителен, поскольку обеспечивает большую сумму доходов в первые два года. Эти дополнительные средства могут быть направлены в оборот и в свою очередь принесут новые доходы.

В-третьих, данный метод не обладает свойствами аддитив­ности. Рассмотрим ситуацию, приведенную в табл. 9.11.

Табл 911 Динамика денежных потоков

Год	Денежные потоки но проектам (vi прд р)
А	Б	В	А и В	Б и В
0-й	-50	-50	-50	-100	-100
1-й
2-й
3-й
Период окупаемости, лет	2,5	1,5	3,5	2,5	3,5

Допустим, что проекты А и Б являются взаимоисключаю­щими, а проект В - независимым. Это означает, что если у предприятия имеются финансовые возможности, то оно мо­жет выбрать не только какой-то один из представленных про­ектов, но и их комбинации, т.е. проекты А и В или проекты Б и В. Если рассматривать каждый проект отдельно с применени­ем показателя «период окупаемости», то можно сделать вывод, что предпочтительным является проект Б. Однако если рас­сматривать комбинации проектов, то следует предпочесть комбинацию из худших проектов А и В.

В то же время существует ряд ситуаций, при которых при­менение метода, основанного на расчете срока окупаемости за­трат, может быть целесообразным. В частности, это ситуация, когда руководство предприятия в большей степени озабочено решением проблемы ликвидности, чтобы инвестиции в инно­вацию окупились и как можно скорее. Метод также хорош в ситуации, когда инвестиции сопряжены с высокой степенью риска, поэтому чем короче срок окупаемости, тем менее риско­ванным является проект. Такая ситуация характерна для от­раслей или видов деятельности, которым присуща большая ве­роятность достаточно быстрых технологических изменений. Таким образом, критерий РР позволяет получить оценки, хотя и грубые, о ликвидности и рисковости инвестиционного про­екта в инновацию. Понятие ликвидности проекта является ус­ловным. Считается, что из двух проектов более ликвиден тот, у которого меньше срок окупаемости. При сравнительной оцен­ке рисковости проектов с помощью критерия РР рассуждаем так: денежные поступления удаленных от начала реализации проекта лет трудно прогнозируемы, т.е. они более рисковы по сравнению с поступлениями первых лет, поэтому из двух про­ектов менее рисковым является тот, у которого меньше срок окупаемости.

Метод расчета коэффициента эффективности инвестиции в инновацию (ARR) имеет две характерные черты:

• он не предполагает дисконтирования показателей дохода;

• доход характеризуется показателем чистой прибыли PN.

Алгоритм расчета исключительно прост, что обусловлива­ет возможность широкого использования этого показателя на практике: коэффициент эффективности (ARR) рассчитывает­ся делением среднегодовой прибыли PN на среднюю величину инвестиции в инновацию (коэффициент берется в процентах). Средняя величина инвестиции в инновацию находится деле­нием исходной суммы капитальных вложений на 2, если пред­полагается, что по истечении срока реализации анализируемо­го проекта все капитальные затраты будут списаны. Если же допускается наличие остаточной или ликвидационной стои­мости (RV), то ее оценка должна быть исключена:

Данный показатель сравнивается с коэффициентом рента­бельности авансированного капитала, рассчитываемого деле­нием общей суммы прибыли предприятия на общую сумму средств, авансированных в его деятельность (среднюю).

В принципе, возможно и установление специального поро­гового значения, с которым будет сравниваться ARR, или даже их системы, дифференцированной по видам проектов, степени риска, центрам собственности и др.

Метод, основанный на коэффициенте эффективности ин­вестиции в инновацию, также имеет ряд существенных недо­статков, обусловленных в основном тем, что он не учитывает временной компоненты денежных потоков. В частности, метод не предполагает учет различия между проектами с одинаковой суммой среднегодовой прибыли, но варьирующей суммой прибыли по годам, а также между проектами, имеющими оди­наковую среднегодовую прибыль, но генерируемую в течение различного количества лет и т.п.

Метод расчета чистого приведенного эффекта (NPV) осно­ван на сопоставлении величины исходной инвестиции (1С) в инновацию с общей суммой дисконтированных чистых денеж­ных поступлений, генерируемых ею в течение прогнозируемо­го срока. Поскольку приток денежных средств распределен во времени, то он дисконтируется с помощью коэффициента г, устанавливаемого аналитиком (инвестором) самостоятельно исходя из ежегодного процента возврата, который он хочет или может иметь на инвестируемый им капитал.

Допустим, делается прогноз, что инвестиция (IС) будет гене­рировать в течение п лет годовые доходы в размере P₁, Р₂, Р₃,..., Р_n- Общая накопленная величина дисконтируемых доходов (PV) и чистый приведенный эффект (NPV) соответственно рассчи­тываются по формулам (9.5) и (9.6):

Очевидно, что если:

NPV> О, то инновационный проект следует принять;

NPV< О, то инновационный проект следует отвергнуть;

NPV = 0, то инновационный проект ни прибыльный, ни убыточный.

При прогнозировании доходов по годам необходимо, по возможности, учитывать все виды поступлений как произ­водственного, так и непроизводственного характера, которые могут быть ассоциированы с данным инновационным проек­том. Так, если по окончании периода реализации проекта пла­нируется поступление средств в виде ликвидационной стои­мости оборудования или высвобождения части оборотных средств, то они должны быть учтены как доходы соответству­ющих периодов.

Если проект предполагает не разовую инвестицию в инно­вацию, а последовательное инвестирование финансовых ре­сурсов в течение т лет, то формула для расчета чистого приве­денного эффекта модифицируется следующим образом:

где i - прогнозируемый средний уровень инфляции.

Расчет с помощью приведенных формул вручную достаточ­но трудоемок, поэтому для удобства применения этого и дру­гих методов, основанных на дисконтированных оценках, целе­сообразно разрабатывать и использовать специальные статис­тические таблицы, в которых табулируются значения сложных процентов, дисконтирующих множителей, дисконтированного значения денежной единицы и т.п. в зависимости от временно­го интервала и значения коэффициента дисконтирования.

При расчете чистого приведенного эффекта NPV, как прави­ло, используется постоянная ставка дисконтирования, однако при некоторых обстоятельствах, например, ожидается измене-

ние уровня учетных ставок, могут использоваться индивидуа­лизированные по годам коэффициенты дисконтирования Ес­ли в ходе имитационных расчетов приходится применять раз­личные коэффициенты дисконтирования, то, во-первых, фор­мула (9 6) неприменима и, во-вторых, проект, приемлемый при постоянной дисконтной ставке, может стать неприемлемым.

Пример

Требуется проанализировать инвестиционный проект в инновацию со следующими характеристиками (млрд р) - 156,40, 70, 70, 50

Рассмотрим два случая а) цена капитала - 13%, 6) ожидается, что цена ка­питала будет меняться по годам следующим образом 11%, 12%, 13%, 14%

а) Воспользуемся формулой 9 6

В этом случае инвестиционный проект в инновацию неприемлем

Показатель чистого приведенного эффекта отражает про­гнозную оценку изменения экономического потенциала пред­приятия в случае принятия рассматриваемого инвестицион­ного проекта в инновацию Этот показатель аддитивен во вре­менном аспекте, т.е. чистые приведенные эффекты различных проектов можно суммировать. Это очень важное свойство, вы­деляющее этот критерий из всех остальных и позволяющее ис­пользовать его в качестве основного при анализе оптимальнос­ти инвестиционного портфеля в инновационные проекты

Очевидно, что если PI > 1, то инновационный проект следует принять,

Метод расчета индекса рентабельности инвестиции в инно­вацию является следствием метода расчета чистого приведен­ного эффекта Этот индекс рентабельности (РГ) рассчитывает­ся по формуле:

PI< 1, то инновационный проект необходимо отвергнуть;

Р1= 1, то инновационный проект не является ни прибыль­ным, ни убыточным.

В отличие от чистого приведенного эффекта индекс рента­бельности является относительным показателем. Благодаря этому он очень удобен при выборе одного проекта из ряда аль-| тернативных, имеющих примерно одинаковые значения чис­тых приведенных эффектов (в частности, если два инноваци­онных проекта имеют одинаковые значения чистых приведен­ных эффектов, но разные объемы требуемых инвестиций, то очевидно, что выгоднее тот из них, который обеспечивает большую эффективность вложений), либо при комплектова­нии портфеля инвестиций в инновации с максимальным сум­марным значением чистых приведенных эффектов.

В методе расчета внутренней нормы рентабельности инвес­тиции в инновацию (IRR) под указанной нормой рентабель­ности понимают значение коэффициента дисконтирования r, при котором NPV проекта равен нулю:

Смысл расчета этого коэффициента при анализе эффектив­ности планируемых инвестиций в инновацию заключается в следующем: IRR показывает ожидаемую доходность проекта, а следовательно, максимально допустимый относительный уро­вень расходов, которые могут быть ассоциированы с данным проектом Например, если проект полностью финансируется за счет ссуды коммерческого банка, значение IRR показывает верх­нюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

На практике любое предприятие финансирует свою де­ятельность, в том числе и инновационную, из различных ис-

точников, в частности из внешних. В качестве платы за пользо­вание авансированными в деятельность предприятия финан­совыми ресурсами оно уплачивает проценты, дивиденды, воз­награждения и т.п., т.е. несет некоторые обоснованные расходы на поддержание своего экономического потенциала. Показатель, характеризующий относительный уровень этих расходов, можно назвать «ценой» авансированного капитала (СО- Этот показатель отражает сложившийся на предпри­ятии минимум возврата на вложенный в его деятельность ка­питал, его рентабельность и рассчитывается по формуле сред­ней арифметической взвешенной.

Экономический смысл этого показателя заключается в сле­дующем: предприятие может принимать любые решения ин­вестиционного характера в инновацию, уровень рентабельнос­ти которых не ниже текущего значения показателя СС {пли це­ны источника средств для данного проекта, если он имеет це­левой источник). Именно с ним сравнивается показатель IRR, рассчитанный для конкретного проекта. Эта связь будет сле­дующей: если IRR > СС, то инновационный проект следует принять; IRR < СС, то инновационный проект следует отвергнуть; IRR = СС, то инновационный проект не является ни прибыль­ным, ни убыточным.

Практическое применение данного метода осложнено, если в распоряжении аналитика нет специализированного финан­сового калькулятора. В этом случае применяется метод после­довательных операций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц выбираются два значения коэффициента дисконтиро­вания r₁ < r ₂ таким образом, чтобы в интервале (r₁, r₂) функция NPV = f (r) меняла свое значение с «+» на«-» или с «-» на «+». Далее применяют формулу

Требуется рассчитать значение показателя IRR для инвес­тиционного проекта в инновацию, рассчитанного на три года, требующего инвестиций в размере 12 млрд р. и имеющего предполагаемые денежные поступления в размере 4 млрд р., 5 млрд р., 8 млрд р.

Возьмем два произвольных значения коэффициента дискон­тирования: r = 9%, r= 19%. Соответствующие расчеты с исполь­зованием табулированных значений на основе формул 9.5-9.7 приведены в табл. 9.12.

Можно уточнить полученное значение. Допускаем, что пу­тем нескольких итераций мы определили ближайшие целые значения коэффициента дисконтирования, при которых NPV меняет знак

Как видим, метод последовательных итераций обеспечива­ет весьма высокую точность (отметим, что с практической точ­ки зрения такая точность является излишней). Свод всех вы­числений приведен в табл. 9.12. Рассмотренная методика применима лишь к акционерным об­ществам. На предприятиях, не являющихся акционерными, анало­гом показателя СС является уровень издержек производства и об­ращения в процентах к общей сумме авансированного капитала

Между показателями NPV, PI, IRR, СС имеются следующие взаимосвязи:

если NPV> О, то одновременно IRR > СС и Р1>1;

если NPV< 0, то одновременно IRR< СС и Р1< 1;

если NPV = 0, то одновременно IRR = СС и Р1= 1.

Основной недостаток, присущий внутренней норме рента­бельности инвестиции в инновацию (IRR) в отношении оцен­ки проектов с неординарными денежными потоками, не явля­ется критическим и может быть преодолен. Соответствующий аналог IRR, который может применяться при анализе любых проектов, называется модифицированной внутренней нормой рентабельности инвестиции в инновацию (MIRR). Алгоритм расчета предусматривает выполнение нескольких процедур. Прежде всего рассчитываются суммарная дисконтированная стоимость всех оттоков и суммарная наращенная стоимость всех притоков, причем и дисконтирование и наращение осу­ществляются по цене источника финансирования проекта. На­ращенная стоимость притоков называется терминальной сто­имостью. Затем определяется ставка дисконтирования, урав­нивающая суммарную приведенную стоимость оттоков и тер­минальную стоимость, которая в данном случае как раз и представляет собой MIRR Общая формула расчета имеет вид:

где 0F_i - отток денежных средств в i-м периоде (по абсолют­ной величине), IF_i - приток денежных средств в i-м периоде; r - стоимость источника финансирования данного проекта в инновацию, п - продолжительность проекта

Формула имеет смысл, если терминальная стоимость пре­вышает сумму дисконтированных оттоков

Критерий модифицированной внутренней нормы рентабель­ности инвестиции в инновацию (MIRR) в полной мере согласу­ется с критерием чистого приведенного эффекта (NPV) и потому может быть использован для оценки независимых проектов Что касается альтернативных проектов, то противоречия между кри­териями NPV и MIRR могут возникать, если проекты существен­но разнятся по масштабу, т е значения элементов у одного пото­ка значительно больше по абсолютной величине, чем у другого, либо проекты имеют различную продолжительность В таком случае целесообразно применять критерий NPV, не забывая од­новременно об учете рисковости денежного потока

В реальной жизни вполне вероятна ситуация, когда необходи­мо сравнивать инвестиционные проекты в инновацию различной продолжительности Речь идет как о независимых, так и об альтер­нативных проектах В частности, сравнение независимых проек­тов может иметь место, когда заранее не известен объем доступных источников финансирования В этом случае проводится ранжиро­вание проектов по степени их приоритетности, т е они как бы вы­страиваются в очередь - по мере появления финансовых возмож­ностей проекты последовательно принимаются к внедрению

Суммарный чистый приведенный эффект (NPV) повторя­ющегося инновационного проекта рассчитывается по формуле

где NPV(i) - чистый приведенный эффект исходного проекта в инновацию, i - продолжительность этого проекта, r- ставка дисконтирования в долях единицы, N - наименьшее общее кратное, п - число повторений исходного проекта (оно харак­теризует число слагаемых в скобках)

Данную методику можно упростить в вычислительном плане. Так, если анализируется несколько проектов, сущест­венно различающихся по продолжительности реализации, то расчеты могут быть достаточно утомительными. Их можно уменьшить, если предположить, что каждый из альтернатив­ных проектов может быть реализован неограниченное число раз. В этом случае при п —> o о число слагаемых в формуле рас­чета NPV (t, п) будет стремиться к бесконечности, а значение NPV(t, оо) может быть найдено по известной формуле для бес­конечно убывающей геометрической прогрессии:

Из двух сравниваемых инвестиционных проектов в инно­вацию проект, имеющий большее значение NPV(i, со), являет­ся предпочтительным.

Существует также и такой подход. Рассчитывают чистый приведенный эффект (NPV) однократной реализации каждого проекта. Для каждого проекта находят эквивалентный срочный аннуитет (будущую стоимость FV_pst исходного денежного пото­ка), приведенная стоимость которого в точности равна NPVnpo-екта. При этом считается, что генерируемые в рамках одного временного периода поступления имеют место либо в его нача­ле, либо в его конце, т.е. они не распределены внутри периода, а сконцентрированы на одной из его границ. В первом случае по­ток называется потоком пренумерандо, или авансовым, во вто­ром - потоком постнумерандо. Наращенный денежный поток C₁, С₂, Сз,..., С„ для исходного потока постнумерандо имеет вид:

а будущая стоимость FV_pst исходного денежного потока (ан­нуитета) постнумерандо может быть оценена как сумма нара­щенных поступлений, иными словами^-

В обратной задаче подразумевается оценка с позиции теку­щего момента, т.е. на конец периода 0. В этом случае реализуется схема дисконтирования, а расчеты необходимо вести по приве­денному потоку. Элементы приведенного денежного потока уже можно суммировать. Их сумма характеризует приведенную, или текущую, стоимость денежного потока, которую при необходи­мости можно сравнивать с величиной первоначальной инвести­ции в инновацию. Следовательно, приведенный денежный по­ток для исходного потока постнумерандо будет иметь вид:

Приведенная стоимость денежного потока постнумерандо PV_pst в общем случае рассчитывается по формуле

Множитель K\(r,k} называется дисконтирующим множи­телем для единичного платежа и определяется по формуле

Если использовать дисконтирующий множитель, то фор­мулу (9. 20) можно записать следующим образом:

Он показывает на текущий момент цену одной денежной единицы будущего, т.е. чему равна одна денежная единица (на­пример, один рубль), циркулирующая в сфере бизнеса k пери­одов от момента расчета при заданной процентной ставке (до­ходности) г и частоте начисления процента.

Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо PV^a_pst выводится из формулы 9.20 и имеет вид:

Множитель K₂(r,n) называется дисконтирующим множи­телем для аннуитета или коэффициентом дисконтирования ренты (аннуитета) и как сумма членов геометрической про­грессии равен величине:

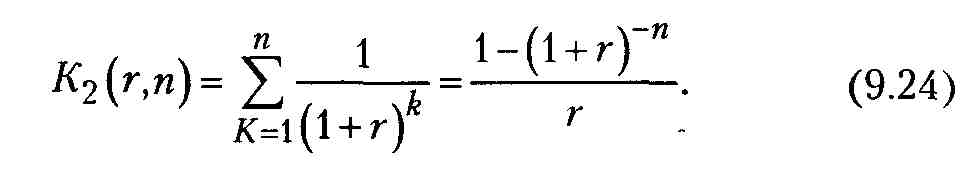
Экономический смысл дисконтирующего множителя K₂(r,n) заключается в том, что он показывает, чему равна с позиции текущего момента величина аннуитета (он пред­ставляет собой частный случай денежного потока или финан­совую ренту) с регулярными денежными поступлениями в размере одной денежной единицы (например, один рубль), продолжающегося п равных периодов с заданной процентной

ставкой r. Дисконтирующий множитель К₂(r,п) полезно ин­терпретировать и как величину капитала, поместив который в банк под сложную процентную ставку г можно обеспечить регулярные выплаты в размере одной денежной единицы в течение п периодов (выплаты производятся в конце каждого периода).

Таким образом, величина аннуитетного платежа (ЕАА) рас­считывается с помощью формулы 9.23. Предполагая, что най­денный аннуитет может быть заменен бессрочным аннуитетом с той же самой величиной аннуитетного платежа, рассчитыва­ют приведенную стоимость бессрочного аннуитета PV^a (оо) по формуле

где А - одно денежное поступление за период (например, год); r- ставка начисления процентов.

Данная формула показывает, что поток даже с неограни­ченным числом платежей имеет все же конечную приведен­ную стоимость. С финансовой точки зрения это понятно, по­скольку деньги, которые поступят через много лет, сейчас ма­ло что стоят (а при высокой инфляции практически ничего не стоят). Эта же ситуация проявляется и при сравнении коэф­фициентов дисконтирования бессрочного аннуитета и аннуи­тетов с большим сроком. Также эта формула используется для оценки целесообразности приобретения бессрочного аннуите­та, если известен размер денежного поступления за период. В качестве г обычно принимается гарантированная процент­ная ставка (например, процент, предлагаемый государствен­ным банком). Инвестиционный проект в инновацию, имею­щий большее значение PV^a (оо), является предпочтительным.

Методам, основанным на повторе исходных проектов, при­суща определенная условность, заключающаяся в молчаливом распространении исходных условий на будущее, что не всегда корректно. Во-первых, далеко не всегда можно сделать точную оценку продолжительности исходного проекта; во-вторых, не очевидно, что проект будет повторяться п-е число раз, особен­но если он сам по себе достаточно продолжителен; в-третьих, условия его реализации в случае повтора могут измениться (это касается как размера инвестиций в инновацию, так и ве­личины прогнозируемых чистых доходов); в-четвертых, рас­четы во всех рассмотренных методах абсолютно формализова­ны, при этом не учитываются различные факторы, которые яв­ляются либо не формализованными, либо имеют общеэконо­мическую природу (инфляция, научно-технический прогресс, изменение технологий, заложенных в основу исходного проек­та, и др.) и т.п. Поэтому к применению подобных методов нуж­но подходить осознанно в связи с тем, что если исходным па­раметрам сравниваемых проектов свойственна достаточно вы­сокая неопределенность, то можно не принимать во внимание различие в продолжительности их действия и ограничиться расчетом стандартных критериев.

В анализе эффективности инновационных проектов необ­ходимо по возможности (или если целесообразно) учитывать влияние инфляции. Это можно сделать корректировкой на ин­декс инфляции (i) либо будущих поступлений, либо ставки

дисконтирования. Наиболее корректной, но и более трудоем­кой в расчетах является методика, предусматривающая кор­ректировку всех факторов, влияющих на денежные потоки сравниваемых проектов. Основными факторами являются пе­ременные расходы и объем выручки. Корректировка может осуществляться с использованием различных индексов, по­скольку индексы цен на продукцию коммерческой организа­ции и потребляемое ею сырье могут существенно отличаться от индекса инфляции. С помощью таких пересчетов исчисляются новые денежные потоки, которые и сравниваются между собой с помощью критерия чистого приведенного эффекта (NPV).

Более простой является методика корректировки ставки дисконтирования на индекс инфляции. Прежде всего рассмот­рим логику такой корректировки на простейшем примере.

Дата добавления: 2014-11-06