Формальні методи багатокритеріального прийняття рішень

Загальна постановка задачі БПР у формальному виді полягає в наступному: знайти такі x₁,…,x_n, приналежні визначеної області G, при яких

z_j (x₁,…,x_n)Þmax, де j=1,..., m (6.1)

при кращому співвідношенні між ними в крапці екстремуму.

У залежності від введених додаткових критеріїв розрізняють ряд неформальних і формальних методів БПР.

До неформального відноситься в першу чергу метод компенсації. Ідея компромісу, зрівноважування по корисності оцінок різних критеріїв, досить розповсюджена. Уперше вона була викладена в 1772 році Б. Франкліним у приватному листі. Він відзначав, що при порівнянні важко одночасно “тримати в голові” усі переваги і недоліки кожного варіанта рішення. Тому зручно виписати у виді двох окремих списків переваги і недоліки варіантів, ретельно проаналізувати, який недолік (чи їхня сукупність) можна вважати еквівалентним визначеній перевазі, а потім викреслити цей пари зі списку.

Розглянемо тепер формальні методи.

Метод виділення головного критерію.

У цьому методі з використанням інформації ОПР формується критерій, на підставі використання якого критерій d вибирається в якості «головного», інші переводяться до складу обмежень і вказуються границі, у яких ці критерії можуть знаходитися.

Задача в даному випадку ставиться в такий спосіб: знайти такі x₁,…,x_n, приналежні області G, при яких

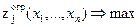
Недолік методу очевидний: нема рації проводити глибоке системне дослідження, якщо всі критерії, крім одного, не враховуються.

Метод лексикографічної оптимізації.

У методі лексикографічної оптимізації передбачається, що використовується критерій, на підставі якого вихідні критерії, можуть бути упорядковані на основі відносини абсолютної переваги. Нехай критерії пронумеровані так, що найбільш важливому з них відповідає номер 1. Тоді на першому кроці вибирається підмножина варіантів рішень, що мають найкращі оцінки за першим критерієм. Якщо виявиться, що таких варіантів тільки один, він і визнається найкращим. Якщо варіантів більше одного, то на другому кроці вибирається підмножина варіантів, що мають найкращі оцінки за другим критерієм, і так далі, доти, поки не буде виявлений кращий варіант.

При пошуку рішення задачі БПР в описаній процедурі, як правило, будуть використовуватися не усі, а лише найбільш важливі критерії, що не завжди може бути виправдано.

Метод послідовних поступок.

В методі послідовних поступок у порівнянні з методом лексикографічної оптимізації вводиться додатковий критерій, при використанні якого для кожного з функціоналів призначається допустиме відхилення значення функціонала від найкращого. Потім на першому кроці виробляється побудова підмножини варіантів рішень, для яких відхилення оцінки за першим критерієм від його екстремального значення не перевищує допустимого відхилення («поступки»). Далі будується підмножина варіантів рішень на основі другого критерію і його поступки і т.д. При цьому поступки призначаються таким чином, щоб тільки на m-ом кроці повинен бути визначений один варіант рішення. Якщо один варіант отриманий на j – ом кроці, причому j < m, то інші m - j критеріїв фактично не використовуються.

Серйозний недолік даного методу – визначення критеріїв, що дозволяють установити величину поступок.

Методи формування скалярного критерію.

У цих методах первісна задача (1) заміняється задачею визначення екстремального (мінімального чи максимального) значення функціонала F*(x₁,…,x_n)=F(z₁(x₁,…,x_n),…,z_m(x₁,…,x_n))=F(z₁,…,z_m), що представляє собою деяку залежність від значень компонентів кожного критерію.

Основною проблемою цього підходу саме і є побудова функції F(.), називаної згортка. Дана проблема розпадається на чотири задачі:

1. Обґрунтування критерію допустимості згортки.

2. Нормалізація критеріїв для їхнього зіставлення.

3. Формування критерію пріоритетів (важливості) приватних критеріїв.

4. Побудова функції згортки.

Критерій допустимості згортки дозволяє установити, що розглянуті частки критерії є однорідними. Якщо ж існує кілька груп однорідних показників, то дозволяється згортка критеріїв, що входять в узагальнений критерій для кожної групи окремо. Згортка критеріїв з різних груп може привести до утрати фізичного й економічного змісту такого критерію.

При нормалізації вибирається критерій, що дозволяє обробити характеристики приватних критеріїв, обмірюваних у різних шкалах. На підставі формування критерію пріоритетів (важливості) приватних критеріїв визначається вектор коефіцієнтів важливості критеріїв

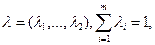
де 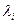- коефіцієнт важливості критерію z_i.

Визначення коефіцієнтів важливості критеріїв, стикається із серйозними труднощами і зводиться або до використання формальних процедур, або до застосування експертних оцінок.

Необхідно звернути увага на висловлення відомого вченого Е.С. Вентцель, що відзначила, що задача визначення важливості критеріїв підмінює багатокритеріальну задачу більш складною в багатьох випадках, чим вихідна задача БПР[46].

При побудові функції згортки часто використовуються адитивна і мультиплікативна згортка компонентів приватних критеріїв. При формуванні критерію доцільності адитивної згортки ґрунтуються на використанні принципу справедливої компенсації абсолютних значень нормованих приватних критеріїв.

Сформулюємо суть цього принципу: справедливим варто вважати такий компроміс, при якому сумарний рівень абсолютного зниження значень одного чи декількох приватних критеріїв не перевищує сумарного рівня абсолютного збільшення значень інших критеріїв. Головний недолік адитивних критеріїв полягає в тому, що вони не випливають з об'єктивної ролі приватних критеріїв у прийнятті рішень і виступають тому як формальний математичний прийом, що додає задачі зручний вид. Крім того, низькі оцінки по одним критеріях можуть компенсуватися високими оцінками за іншими критеріями. Це значить, що зменшення одного з критеріїв аж до нульового значення може бути покрито зростанням іншого критерію. Функція F(z₁,…,z_m)у даному випадку представляється у виді прямої згортки:

; чи нормованої згортки:

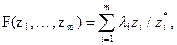
де - оптимальне значення i – го критерію.

Коефіцієнти 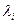зв'язані умовою:

Мультиплікативна згортка критерію F(z₁,…,z_m) складається в представленні його у виді добутку:

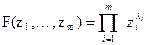
Мультиплікативний критерій утвориться шляхом простого перемножування приватних критеріїв z_i зведених у ступені 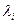. Якщо всі приватні критерії мають однакову важливість, то . При різній важливості критеріїв .

У мультиплікативних критеріях схема компромісу припускає операції не з абсолютними, а з відносними змінами приватних критеріїв.

Правомочність мультиплікативного критерію ґрунтується на принципі справедливої відносної компенсації: справедливим варто вважати такий компроміс, при якому сумарний рівень відносного зниження значень одного чи декількох критеріїв не перевищує сумарного рівня відносного збільшення значень інших критеріїв.

Достоїнством мультиплікативного критерію є те, що при його використанні не потрібно нормування приватних критеріїв. Недоліки полягають у тому, що компенсація недостатньої величини одного приватного компенсується надлишковою величиною іншого і має тенденцію згладжувати рівні приватних критеріїв за рахунок нерівнозначних первісних значень приватних критеріїв.

Крім цих двох зазначених критеріїв у теорії БПР особливе місце займає критерій, що реалізує принцип компромісу, що заснований на ідеї рівномірності.

Якщо із суті задачі БПР випливає повна неприпустимість компенсації значень одних критеріїв іншими, тобто потрібно забезпечити рівномірне підтягування всіх критеріїв до найкращого рівня, то використовують функцію F(z₁,…,z_m)наступного виду:

Такий критерій використовується в економіці при рішенні задач планування по «вузькому місцеві».

Якщо із суті задачі БПР випливає, що одні критерії бажано збільшувати, а інші зменшувати, то іноді використовують функцію F(z₁,…,z_m)у виді відносини одних критеріїв до інших, наприклад:

де і=1,...,m1 – номера критеріїв, які необхідно максимізувати, а і=m1,...,m2 – номера критеріїв, які необхідно зменшувати.

Часто перша група критеріїв ототожнюється з цільовим ефектом, а друга - з витратами на його досягнення. При цьому критерії не повинні бути однорідними.

Метод наближення до «ідеальної крапки»

Суть даного методу полягає в тім, що як критерій БПР використовується положення про мінімізацію відхилення від «ідеальної крапки», у якості якої використовується крапка з координатами, що відповідають екстремальним значенням кожного критерію.

Нехай z_j ^*(x₁,…,x_n),j=1,…,m–максимальне значення кожного критерію. Задача в даному випадку ставиться в такий спосіб: знайти такі x₁,…,x_n,преналежні області G, при яких

Þ min

Метод Волковича [47].

Суть даного методу полягає у тому, що у якості критерію БПР використовується положення про мінімізацію нормованого щодо кожного критерію відхилення від «ідеальної крапки». Істотним достоїнством цього методу є те, що він не залежний від розмірності кожного критерію

Задача в даному випадку ставиться в такий спосіб: знайти такі x₁,…,x_n, приналежні області G, при яких

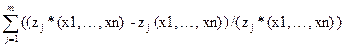Þ min

Розглянуті групи методів надають широкі можливості для аналізу БПР, однак критерії застосовності тих чи інших методів внаслідок евристичного характеру останніх не можуть бути чітко сформульовані. Від цього недоліку вільна група методів, що ґрунтуються на аксіоматичному підході до прийняття рішень - теорії корисності.

У теорії корисності виходять з того, що додатковий критерій призначений для виявлення порядку переваг на альтернативах (результату прийняття рішень по окремому варіанті), що дозволяє забезпечити обґрунтований вибір.

Виявити формальне відношення чи переваги байдужності безпосереднім порівнянням альтернатив важко: показники результату операції численні, мають різний фізичний зміст і різні шкали вимірів (вартість виготовлення, чисельність обслуговуючого персоналу, кількість клієнтів і т.п.). Оскільки немає універсальної міри, що володіє фізичним змістом і дозволяє порівняти результати варіантів по нерівномірній шкалі, а потреба в ній існує, то вводиться штучна міра, що визначається через корисність альтернатив (результатів). Більшість ОПР використовують порівняно простий підхід до оцінки альтернатив упорядкування їхній по зростанню корисності від найменш корисних до найбільш корисних. Своє відношення до альтернатив ОПР можуть виразити і кількісно, приписавши кожному результату деяке число, що визначає його відносну перевагу. Наприклад, найменш корисний результат може бути відбитий числом 1, що випливає числом 2 і т.д., до найбільш корисного результату.

Таким чином, корисність - це дійсне число, приписуване результату операції, яке характеризує його переваги в порівнянні з іншими щодо мети. Знаючи можливі альтернативи з їхніми показниками корисності, можна побудувати функцію корисності, що дає основу для порівняння і вибору рішень. У теорії корисності доводиться, що при цілком природних допущеннях щодо переваг ОПР така функція існує. Переваги ОПР формулюються у виді аксіом. Оскільки системи переваг у різних ОПР можуть розрізнятися, те різні аксіоматики приводять до різних видів згортки і, отже, функція корисності не єдина. Причина полягає в тім, що відсутні визначення нульової корисності, одиниці корисності і шкали корисності (можна довільно вибирати нуль, одиницю і шкали виміру корисності альтернатив).

Розглянемо основні аксіоми теорії корисності.

Аксіома 1. Вимірність. Кожному альтернативному результату може бути поставлене у відповідність ненегативне дійсне число р., розглянуте як міра відносної корисності результату.

Аксіома 2. Порівнянність. Будь-які два результати порівнянні: або один результат переважніше іншого, або результати однаково кращі (еквівалентні). Аксіома заснована на допущенні: на безлічі альтернатив існує зроблене, рефлексивне і транзитивне відношення слабкої переваги.

Аксіома 3. Транзитивність. Співвідношення переваги й еквівалентності результати транзитивні. Якщо результат а₁ переважніше результату а₂, а результат а₃ переважніше результати a₃, то результат a₁ теж переважніше результату a₃. Аналогічно, якщо результат а₁ еквівалентний результату а₂, а результат а₂ еквівалентний результату a₃, те результат а₁ і a₃ теж еквівалентні.

Аксіома 4. Комутативність. Перевага результату a_i результату а_j не залежить від порядку, у якому вони названі і представлені.

Аксіома 5. Незалежність. Якщо результат a_i переважніше результату a_j і, крім того, існує результат a_k, що не оцінюється відносно результатів a_ij і a_jk, то суміш результатів a_i і a_k переважніше суміші результатів a_j і a_k. (Під сумішшю результатів a_i і a_j розуміється результат, що полягає в появі одного з них з деякою імовірністю, наприклад результату a_i з імовірністю p, а результату a_j з додатковою імовірністю 1 - p).

Відповідно до теорії корисності при виконанні в реальній задачі оцінки систем усіх п'яти аксіом існує функція корисності, однозначно визначена на безлічі всіх альтернатив з точністю до монотонного строго зростаючого лінійного перетворення, інакше корисність виміряється в шкалі інтервалів. Важливо підкреслити, що функція корисності характеризує лише відносну, а не абсолютну перевагу альтернатив.

Достоїнство способу відносно висока об'єктивність. Суб'єктивні моменти в оцінку корисності хоча і вносяться, але не прямо, як при інших способах, а непрямим образом. Основний же недолік складається в труднощах реалізації.

Дата добавления: 2014-11-06