Оптимальність по Парето і Слейтеру

Одними із широко використовуваних критеріїв допустимості, що застосовуються для рішення задач БПР, є критерії Парето і Слейтера.

Сутність критерію Парето полягає в наступному. Крапка з координатами (z₁^п,…,z_m^п) у просторі критеріїв оптимальна по Парето, щодо крапки з координатами (z₁,…,z_m),якщо виконуються наступне умова:

При цьому хоча б одне з нерівностей виконується як строга нерівність.

Критерій Парето дає можливість сформувати поняття множини Парето (переговорна множина, множина компромісів) G* як підмножина множини G варіантів рішень. У випадку, якщо множина Парето відображена у визначеному просторі, те його визначають як область Парето. Множина G* задається властивістю його елементів. Крапка з координатами (z₁^п,…,z_m^п) у просторі критеріїв належить множині Парето, якщо не існує такої крапки з координатами (z₁,…,z_m),для який виконуються наступне умова:

При цьому хоча б одне з нерівностей виконується як строга нерівність.

Зміст даного вираження визначає принцип Парето, що полягає в наступному. Множина Парето включає варіанти рішень, що завжди більш кращі в порівнянні з іншими варіантами, що не входять у множину Парето. При цьому будь-які два варіанти з множині Парето по перевазі непорівнянні.

Для визначення області Парето береться визначена крапка і будується аналог двовимірного кута, причому якщо усередині чи на границі є хоча б одна крапка, те аналізована не належить області Парето. Розглянемо приклад побудови області Парето на базі допустимих рішень у просторі критеріїв {z₁, z₂ }, що представлено на рис. 6.3.

Для цього необхідно виділити крапки з області G щодо який немає крапок, оптимальних по Парето. Крапка c є оптимальної по Парето щодо крапок a і b, тому що вона знаходиться на одній стороні кутів з вершинами в цих крапках. Кут з вершиною в крапках c, d і e інших крапок області G не містить. Крапка e оптимальна по Парето щодо крапок f і g, тому що знаходиться усередині кутів, побудованих з цих крапок, а також щодо крапки h, тому що знаходиться на одній стороні кута, побудованого з цієї крапки. Щодо крапки і немає крапок, оптимальних по Парето. У той же час ця крапка є оптимальної по Парето щодо крапки j. Щодо крапок k і l немає крапок, оптимальних по Парето. Щодо крапок m, n і o є безліч внутрішніх крапок області G, оптимальних по Парето щодо них.

Це дозволяє установити, що область Парето складається з наступних відрізків: [c,e]; [h,і] (без крапки h); [j,l] (без крапки j).

Сутність критерію Слейтера полягає в наступному. Крапка з координатами (z₁^п,…,z_m^п) у просторі критеріїв оптимальна по Слейтер, щодо крапки з координатами (z₁,…,z_m),якщо виконуються наступне умова:

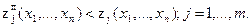
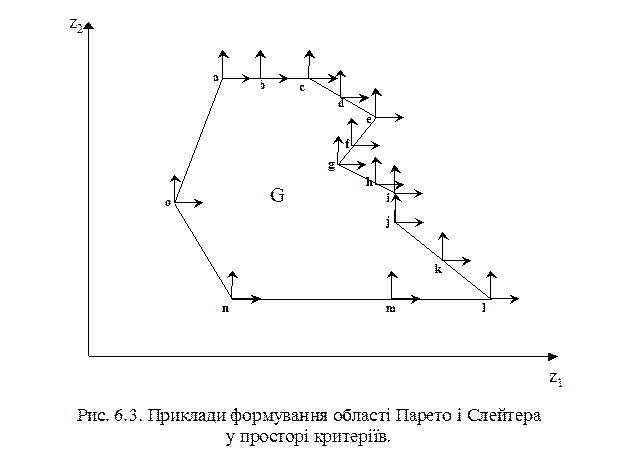
Критерій Слейтера дає можливість сформувати поняття множини Слейтера (переговорна множина, множина компромісів) G* як підмножина множини G варіантів рішень. У випадку, якщо множина Слейтера відображена у визначеному просторі, те його визначають як область Слейтера. Множина G* задається властивістю його елементів. Крапка з координатами (z₁^п,…,z_m^п) у просторі критеріїв належить множині Слейтера, якщо не існує такої крапки з координатами (z₁,…,z_m),для який виконуються наступне умова:

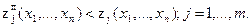
Зміст даного вираження визначає принцип Слейтера, що полягає в наступному. Множина Слейтера включає варіанти рішень, що завжди більш кращі в порівнянні з іншими варіантами, що не входять у множину Слейтера. При цьому будь-які два варіанти з множині Слейтера по перевазі непорівнянні.

Для визначення області Слейтера береться визначена крапка і будується аналог двовимірного кута, причому якщо усередині є хоча б одна крапка, те аналізована не належить області Слейтера. Розглянемо приклад побудови області Слейтера на базі допустимих рішень у просторі критеріїв {z₁, z₂ }, що представлено на рис. 6.3.

Для цього необхідно виділити крапки з області G щодо який немає крапок, оптимальних по Слейтеру. Крапка c не є оптимальної по Слейтеру щодо крапок a і b, тому що вона знаходиться на одній стороні кутів з вершинами в цих крапках, а не всередині кута. Кут з вершиною в крапках c, d і e інших крапок області G не містить. Крапка e оптимальна по Слейтеру щодо крапок f і g, тому що знаходиться усередині кутів, побудованих з цих крапок. Крапка e не оптимальна по Слейтеру щодо крапки h, тому що знаходиться на одній стороні кута, побудованого з цієї крапки. Щодо крапки і немає крапок, оптимальних по Слейтеру. У той же час ця крапка не є оптимальною по Слейтера щодо крапки j. Щодо крапок k і l немає крапок, оптимальних по Слейтеру. Щодо крапок m, n і o є безліч внутрішніх крапок області G, оптимальних по Слейтеру щодо них.

Це дозволяє установити, що область Слейтера складається з наступних відрізків:[a,c]; [c,e]; [h,і]; [i,j];[j,l].

Область Слейтера завжди не менше, ніж область Порето. Це порозумівається тим, що умова Слейтера завжди більш тверде в порівнянні з умовою Парето, і тому при його використанні відкидається менша кількість крапок.

Розглянемо питання пошуку області Парето і області Слейтера в пространстві перемінних.

Для рішення цієї задачі використовується поняття градієнта (це вектор, що вказує напрямок максимального росту функції у визначеній крапці) і антиградієнта (напрямку максимального зменшення значення у визначеній крапці).

Складове градієнта – це є часткова похідна функції по кожній з перемінних. У такий спосіб градієнт визначається по формулі:

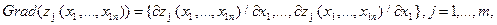
антіградиент визначається по формулі:

Характерною рисою використання градієнта є те, що, здійснюючи визначений крок з вихідної точки в іншу крапку по напрямку градієнта, одержують максимальне збільшення функції в порівнянні з будь-яким іншим напрямком. Використання антиградієнта дає максимальне зменшення функції в порівнянні з будь-яким іншим напрямком. Градієнт і антиградієнт знаходяться на одній прямій у точності, але в різних напрямках. У випадку лінійного функціонала в будь-якій крапці градієнт йде по тому самому напрямку, аналогічна властивість має антиградієнт.

Площина, перпендикулярна напрямку градієнт-антиградієнт, володіє тим властивістю, що на ній значення функціонала однакові, тому що пряма однаково вилучена об початки координат у будь-якій крапці цієї прямої.

У цьому випадку прямий кут з певної точки, на основі якого формувалися області Парето і Слейтера, заміняється на кут між площинами, кожна із яких перпендикулярна напрямку градієнт – антіградієнт по кожному критерію

Розглянемо приклад формування області Парето в просторі перемінних. Нехай задано два критерії згідно формул:

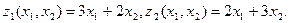
Градіент по кожному критерію має вигляд:

а антіградіент по кожному критерію має вигляд:

На рис. 6.4 наведено приклад формування області Парето у просторі перемінних в випадку, коли початкова область являє собою множину окремих крапок.

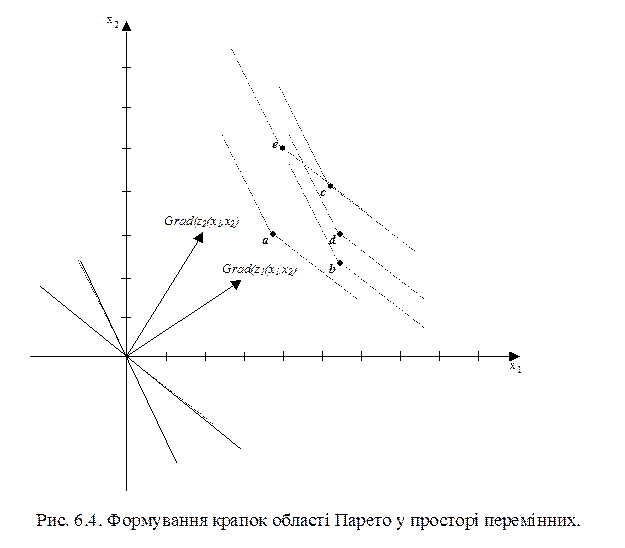
У зв'язку з тим, що розглядається двовимірний випадок, площини перетворяться в прямі. На цьому малюнку кут між прямими, що перпендикулярні напрямку «градієнт – анти градієнт», виділений пунктиром. При цьому щодо крапки a крапки b, c, d і e оптимальні по Парето, тому що знаходяться усередині кута з вершиною в a. Щодо крапки b крапки c і d оптимальні по Парето, тому що знаходяться усередині кута з вершиною в b, а крапка e оптимальна по Парето, тому що знаходиться на одній зі сторін. Щодо крапки c немає крапок, оптимальних по Парето. Щодо крапки d оптимальна по Парето крапка c. Щодо крапки e оптимальна по Парето крапка c, тому що вона знаходиться на одній зі сторін кута з вершиною в крапці e.

Це дозволяє зробити висновок, область Парето в даному випадку складається з однієї крапки c.

Після формування області Парето чи Слейтера можна використовувати раніше викладені формальні методи чи людино-машинні процедури векторної оптимізації.

Достоїнством людино-машинних процедур векторної оптимізації є сполучення можливостей ЕОМ по швидкому проведенню великих розрахунків і здібностей людини до сприйняття альтернатив у цілому, без тривалого вивчення і порівняння їхніх оцінок за окремими критеріями. Загальна схема цих методів полягає в наступному. Тим чи іншому способу ОПР указує свої переваги на безлічі векторних оцінок альтернатив. На основі отриманої інформації ЕОМ автоматично звужує вихідна безліч альтернатив, повідомляючи ОПР по закінченні процесу звуження найкращі альтернативи. Потім ОПР указує припустимі рівні зниження оцінок по одним критеріях, необхідні більш високі рівні оцінок за іншими критеріями, і ЕОМ знову виконує необхідні розрахунки. Ітеративний процес продовжується доти, поки не буде вирішена задача вибору альтернатив. У процесі рішення пошук ведеться серед елементів множини Парето чи Слейтера.

Дата добавления: 2014-11-06