Тема 3. Теория пределов

3.1. Основные понятия

Число является пределом функции при , если для любого, даже сколь угодно малого, положительного числа существует такое положительное число , что для всех 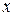, удовлетворяющих условию 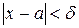, выполняется неравенство

.

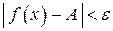(3.1)

Тот факт, что функция при имеет предел, равный , принято обозначать в виде

.

(3.2)

Функция называется бесконечно малой при , если

.

(3.3)

Функция называется бесконечно большой при , если

.

(3.4)

Функция называется ограниченной при , если существует такое положительное число , что для всех значений 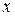из окрестности числа 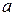выполняется неравенство

.

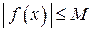(3.5)

Связь между бесконечно большими и бесконечно малыми функциями:

v Если функция при является бесконечно большой, то обратная ей функция 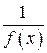будет бесконечно малой (условно: ).

v Если функция 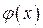при является бесконечно малой, то обратная ей функция будет бесконечно большой, причем предполагается, что в окрестности точки 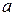функция 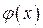в нуль не обращается (условно: ).

Предположим, что функции имеют пределы при . Тогда можно сформулировать следующие правила:

1. Предел постоянной величины равен самой этой постоянной

.

2. Постоянный множитель можно выносить за знак предела

.

3. Предел алгебраической суммы конечного числа функций равен алгебраической сумме пределов слагаемых, если эти пределы существуют

.

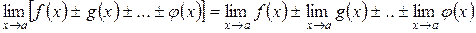4. Предел произведения конечного числа функций равен произведению пределов этих функций, если эти пределы существуют

.

5. Предел частного двух функций равен частному их пределов, если

.

При нахождении предела функции нужно сначала в выражении функции заменить аргумент его предельным значением. Например,

.

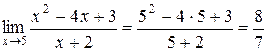3.2. раскрытие неопределенностей

Вычисление предела функции путем подстановки вместо аргумента его предельного значения не всегда возможно, так как часто это приводит к неопределенным выражениям вида 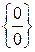; ; ; ; , но из этого не следует, что предел функции не существует. В таких случаях необходимо произвести ряд преобразований, которые позволят оценить предел. Рассмотрим некоторые приемы отыскания пределов в случае неопределенностей.

Неопределенность вида 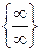возникает при отношении многочленов. Ее раскрывают делением числителя и знаменателя почленно на 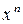, где высшая степень числителя и знаменателя.

Пример 3.1. .

Решение. Оценка числителя и знаменателя при 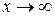приводит к неопределенности 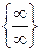. Для решения задачи следует разделить числитель и знаменатель на , а после перейти к непосредственному вычислению предела. Итак,

.

Пример 3.2. .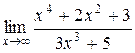

Решение. Здесь наивысшая степень переменной 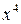, на нее и делят.

Пример 3.3.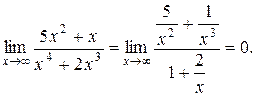

При раскрытии неопределенности вида 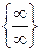полезно запомнить следующие правило:

а) если степень числителя больше степени знаменателя, то предел равен ;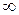

б) если степень числителя меньше степени знаменателя, то предел равен 0;

в) если степень числителя равна степени знаменателя, то предел равен отношению коэффициентов при наивысших степенях в числителе и знаменателе.

Неопределенность вида 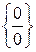при раскрывают разными способами:

а) Если она возникла в результате деления двух многочленов, то ее раскрывают выделением в числителе и знаменателе множителя 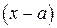и сокращением на него (т.е. разложением на множители и последующим сокращением).

Пример 3.4. Найти .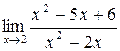

Решение. Непосредственная подстановка предельного значения аргумента приводит к неопределенности 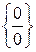. Следовательно, прежде чем перейти к пределу, необходимо данное выражение преобразовать. Числитель и знаменатель данной дроби раскладываем на множители. Имеем: 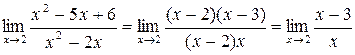. Подставляя в преобразованное выражение предельное значение аргумента, имеем .

б) Для раскрытия неопределенности 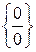, содержащей иррациональные выражения, следует числитель и знаменатель домножить на сопряженное выражение для иррационального, после чего сделать необходимые упрощения и вычислить предел.

Пример 3.5. Найти .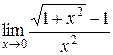

Решение. Если в выражение подставить , то получим неопределенность 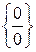. Чтобы ее раскрыть, умножим числитель и знаменатель на выражение, сопряженное числителю. После этого сокращаем на 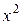и на основании теоремы о пределе дроби имеем:

.

Неопределенность вида , образуемую разностью двух бесконечно больших величин одного знака, раскрывают домножением на сопряженное выражение, приведением к общему знаменателю или вынесением общего множителя. При домножении на сопряженное выражение следует одновременно разделить на него.

Пример 3.6. .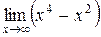

Решение. .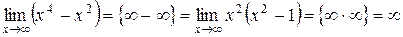

Пример 3.7. .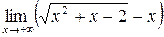

Решение. Домножим и разделим выражение на сопряженное к нему выражение, получим

.

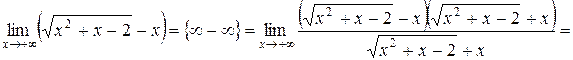
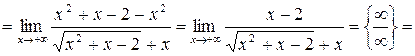
Пример 3.8. .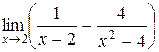

Дата добавления: 2014-11-06