Применение производных для исследования функций

Таблица производных

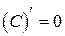
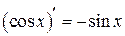
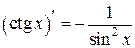
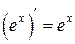
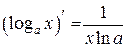
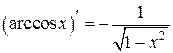
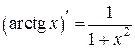
4.3. Основные правила дифференцирования

.

Пример 4.1. Найти производную функции .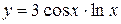

Решение. Применим правило дифференцирования произведения и воспользуемся таблицей производных.

.

Если 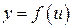, а является функцией независимой переменной 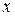: 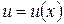, то называется сложной функцией переменной . Переменная при этом называется промежуточной. Производная по 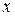функции имеет вид . Аналогичное правило имеет место и в случае, когда сложная функция задается цепочкой, содержащей три и более звена. Например, если 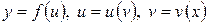, то 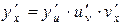. Практическую реализацию этого правила покажем на примерах.

Пример 4.2. Найти производную функции .

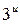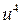Решение. Сначала применим формулу дифференцирования показательной функции , где , затем применим формулу дифференцирования степенной функции , где 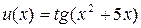, далее - формулу дифференцирования тригонометрической функции , где и, наконец, дифференцируем . В подробной записи это имеет вид:

Пример 4.3. Найти производную функции .

Решение. Применим правило дифференцирования сложной функции и получим

.

Понятие производной можно применять для аналитического исследования свойств функции и построения ее графика.

Областью определения функции 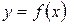называют множество значений аргумента 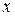, при которых функция определена.

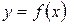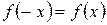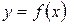Функция называется четной, если выполняется условие . При этом график функции симметричен относительно оси . Функция называется нечетной, если выполняется условие . При этом график функции симметричен относительно начала координат. Если функция 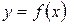не является ни четной, ни нечетной, то эта функция общего вида.

Функция 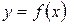называется возрастающей на не­котором интервале, если для любых двух чисел и из этого интервала из неравенства следует неравенство .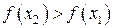

Функция называется убывающей на не­котором интервале, если для любых двух чисел и из этого интервала из неравенства следует неравенство .

Возрастающие или убывающие функции называются монотонными.

Признаки возрастания и убывания функций:

v Если во всех точках некоторого интервала производная , то функция на этом интервале воз­растает.

v Если во всех точках некоторого интервала производная , то функция на этом интервале убывает.

Пример 4.4. Найти интервалы монотонности функции

.

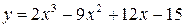Решение. Областью определения данной функции является вся ось 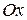. Находим производную . Чтобы найти интервалы возрастания функции, решим неравенство 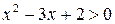; чтобы найти интервалы убывания функции, решим неравенство 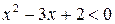. Корни квадратного трёхчлена 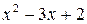равны 1 и 2, поэтому распределение знаков квадратного трехчлена имеет вид

+ – +

1 2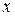

Следовательно, на интервалах 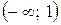и функция возрастает, а на интервале 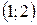функция убывает.

Необходимый признак экстремума: е сли точка 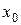является точкой экстремума, то в этой точке производная 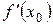равна нулю или не существует.

Точки, в которых первая производная равна нулю, а также, в которых она не существует, но функция сохраняет непрерывность, называются критическими точками первого рода.

Достаточный признак экстремума: е сли при переходе через критическую точку производная меняет знак, то критическая точка является точкой экстремума. Это точка максимума, если производная меняет знак с плюса на минус, и точка минимума, если производная меняет знак с минуса на плюс.

Пример 4.5. Исследовать на экстремум функцию .

Дата добавления: 2014-11-06