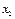Принцип напряжений Коши. Вектор напряжений

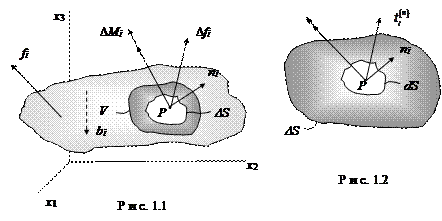
На рис. 1.1 изображена область пространства, занятая материальным континуумом, на который действуют поверхностные силы f_i и массовые силы b_i. Т.к. действие сил передается от одной части среды к другой, материал внутри произвольного объема V, ограниченного поверхностью S, взаимодействует с материалом вне этого объема. Возьмем n_i в качестве единичного вектора внешней нормали в точке Р к малой площадке D S поверхности S и обозначим через 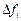результирующую всех поверхностных сил, действующую через площадку D S на материал внутри V со стороны внешней среды. Распределение силы на D S не обязательно однородно, в общем случае это распределение эквивалентно одной силе и моменту, приложенным в точке Р и представленным на рис. 1.1 векторами D f_i и D M_i.

Принцип напряжения Коши утверждает, что отношение 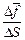стремится к определенному пределу 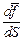, когда D S стягивается в точку Р (т.е. 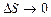), в то время как момент силы 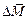относительно точки Р в пределе стремится к нулю (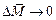, 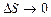). Все теории следующие из принципа Коши носят название безмоментных теорий механики сплошных сред. Если бы момент в точке Р при предельном переходе не обращался в нуль (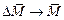, 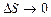), то в этой точке был бы также определен вектор момента (пары) напряжений, изображенный на рис. 1.2 стрелкой с двойным острием. В упругости такие теории носят название моментных теорий механики сплошных сред.

Результирующий вектор 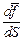(сила, отнесенная к единице площади) называется вектором напряжения в точке Р на площадке D S и обозначается 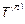(рис. 1.2), где индекс 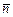указывает на зависимость напряжения от ориентации площадки D S. Совокупность всех векторов напряжений 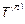в заданной точке и направлений, задаваемых вектором нормали 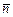, определяют напряженное состояние в точке. Количество таких пар (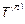, 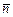) бесконечно.

1.3. Напряженное состояние в точке. Тензор напряжения

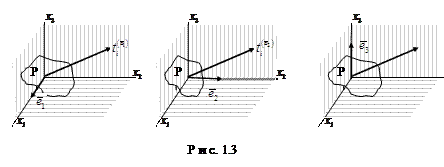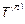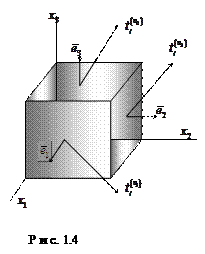
Напряженное состояние в любой точке будет полностью заданным, если заданы три пары векторов (, 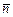) на трех взаимно перпендикулярных площадках. Выберем плоскости, перпендикулярные осям координат, и будем обозначать векторы нормали и напряжения так, как это сделано на рис. 1.3, или рассмотрим схематическое изображение этих трех схем, представленное на рис. 1.4. Каждый из трех векторов напряжения 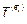на площадках, параллельных координатным плоскостям, можно выразить через их декартовы компоненты

,

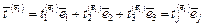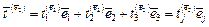, (1.1)

.

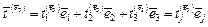Девять компонент векторов напряжения , (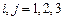) являются компонентами декартова тензора второго ранга, так называемого тензора напряжений.

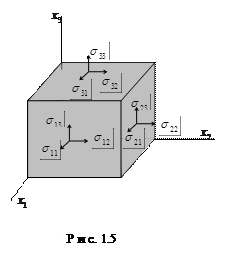
Напряжения, определяемые компонентами тензора напряжений, и координатные плоскости изображены на рис. 1.5. Первый индекс тензора напряжения – i указывает на площадку, имеющую нормаль 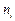, второй индекс j – направление компоненты напряжения на этой площадке вдоль соответствующей оси. Направление компоненты 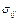выбирается положительным, если нормаль 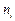совпадает с соответствующим направлением i -ой оси, а действующая сила совпадает с направлением j -ой оси. 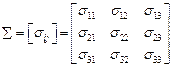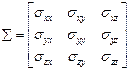Тензор напряжений может быть обозначен , или , или .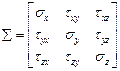

Напряжения 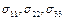, соответствующие перпендикулярным к указанным площадкам силам, называются нормальными напряжениями. Все остальные компоненты напряжений носят название касательных напряжений или напряжений сдвига, чтобы выделить эти компоненты для них часто используют обозначение 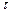вместо .

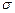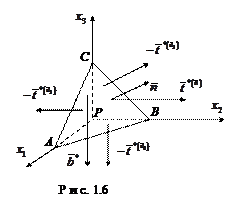1.4. Связь между тензором напряжения и вектором напряжения

Рассмотрим элементарный материальный тетраэдр с вершиной в точке Р рис.1.6. Пусть 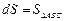, основания тетраэдра, 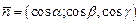– единичный вектор нормали к грани АВС, 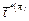– вектор среднего напряжения действующего на основание тетраэдра АВС со стороны внешней среды, 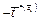– вектор средних сил действующих через боковые грани тетраэдра на внешнюю среду, со стороны материала объема тетраэдра, 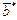– вектор массовых сил. Для равновесия тетраэдра под действием всех этих сил необходимо выполнения равенства:

,

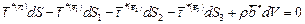где 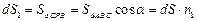, , 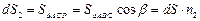, 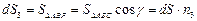–плотность. Устремим линейные размеры тетраэдра пропорционально к нулю, тогда массовые силы будут бесконечно малыми более высокого порядка, чем поверхностные силы, а значит ими можно будет пренебречь. В результате равенство примет вид

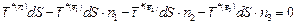
откуда имеем

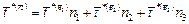или , , .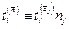

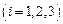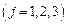Используя обозначение получаем

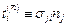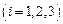, , или 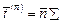, (1.2)

где суммирование ведется по индексу j.

Данное выражение логично представить в матричном виде

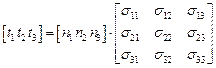(1.3)

или в виде системы линейных уравнений

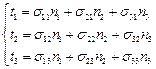(1.4)

Дата добавления: 2014-11-06