
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры с решениями
|
|
|
|
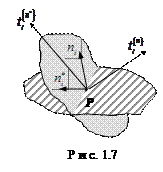
Пример 1.1. Векторы напряжений 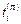 и
и 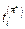 в точке Р действуют соответственно на элементы поверхности
в точке Р действуют соответственно на элементы поверхности 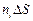 и
и 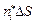 (рис. 1.7). Показать, что компонента
(рис. 1.7). Показать, что компонента 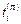 в направлении
в направлении 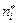 равна компоненте
равна компоненте 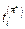 в направлении
в направлении  .
.
Решение. Требуется показать, что  . Используя (1.2), получим
. Используя (1.2), получим  т.к. тензор напряжений симметричен
т.к. тензор напряжений симметричен 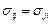 , то данное соотношение можно переписать в виде
, то данное соотношение можно переписать в виде  .
.
Пример 1.2. В некоторой точке тела в декартовой ортогональной системе координат тензор напряжений задан своими компонентами (в Паскалях)
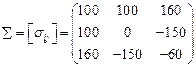
Для площадки с нормалью  , найти компоненты вектора
, найти компоненты вектора 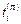 и угол q между вектором напряжения и нормалью.
и угол q между вектором напряжения и нормалью.
Решение. Проверим, является ли вектор нормали единичным, в противном случае его необходимо нормировать: 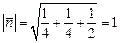 .
.
Используя формулу (1.2), находим
 .
.
Угол q между вектором напряжения и нормалью определим, воспользовавшись формулой скалярного произведения 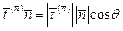 :
:
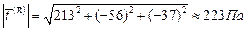 ,
,
 ,
, 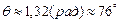 .
.
Ответ: 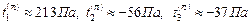 ,
,  .
.
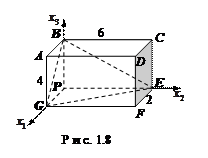 Пример 1.3. В точке Р задан тензор напряжений
Пример 1.3. В точке Р задан тензор напряжений
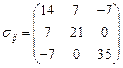 .
.
Определить вектор напряжений в точке Р на площадке параллельной плоскости BGE в элементарном параллелепипеде изображенном на рис.1.8.
Решение. Найдем вектор нормали к изображенной плоскости BGE. Используя уравнение плоскости в отрезках 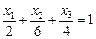 , или
, или 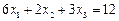 , имеем вектор нормали
, имеем вектор нормали  ,
, 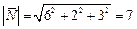 или
или  . Вектор напряжения находим, используя формулу (1.2):
. Вектор напряжения находим, используя формулу (1.2):
 .
.
Ответ:  .
.
Пример 1.4. Тело находится в равновесии под действием только поверхностных сил. Пусть 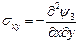 ,
, 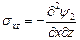 ,
,  , где
, где 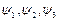 - произвольные, достаточное число раз дифференцируемые функции. Найти все компоненты тензора напряжений, при которых удовлетворяются уравнения равновесия.
- произвольные, достаточное число раз дифференцируемые функции. Найти все компоненты тензора напряжений, при которых удовлетворяются уравнения равновесия.
Решение. Уравнения равновесия 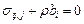 примут вид
примут вид  (
( , т.к. тело находится только под действием только поверхностных сил).
, т.к. тело находится только под действием только поверхностных сил).
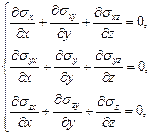 Þ
Þ 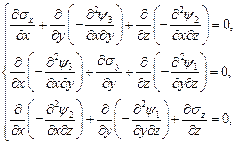 Þ
Þ
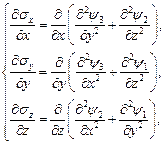 Þ
Þ 
Ответ: 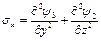 ,
,  ,
, 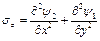 .
.
Пример 1.5. Матрица компонент тензора напряжений в покоящийся среде с заданной плотностью r имеет вид 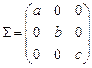 , где a, b, с – сonst. Найти массовые силы, если компоненты тензора напряжений заданы в декартовой, цилиндрической и сферической системах координат.
, где a, b, с – сonst. Найти массовые силы, если компоненты тензора напряжений заданы в декартовой, цилиндрической и сферической системах координат.
Замечание. При изменении системы координат диагональный тензор напряжения не изменится, это свойство будет рассмотрено в следующем разделе.
Решение. 1) Запишем уравнения равновесия в декартовой системе координат и подставим заданный тензор напряжений
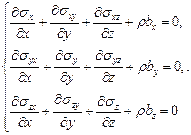 Þ
Þ 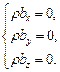 Þ
Þ 
2) Уравнение равновесия в цилиндрической системе координат

где  - проекции объемной силы, отнесенные к единице объема на координатные оси
- проекции объемной силы, отнесенные к единице объема на координатные оси  , а компоненты заданного тензора в цилиндрической системе координат соответствуют следующим напряжениям
, а компоненты заданного тензора в цилиндрической системе координат соответствуют следующим напряжениям 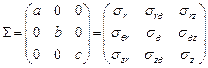 .
.
Поэтому
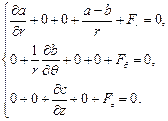 Þ
Þ 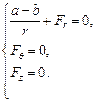 Þ
Þ 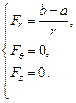
3) Уравнение равновесия в сферической системе координат
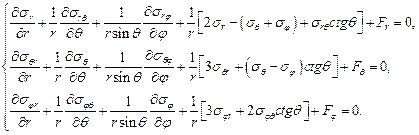
где  - проекции объемной силы, отнесенные к единице объема на координатные оси
- проекции объемной силы, отнесенные к единице объема на координатные оси  . Компоненты тензора напряжений в сферической системе координат соответствуют следующим напряжениям
. Компоненты тензора напряжений в сферической системе координат соответствуют следующим напряжениям  .
.
Поэтому
 Þ
Þ 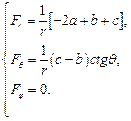
Ответ: 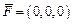 в системе (x y z),
в системе (x y z),  в системе (rq z),
в системе (rq z), 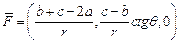 в системе (rqj).
в системе (rqj).
Задания для самостоятельного решения по теме
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 3651; Нарушение авторских прав?; Мы поможем в написании вашей работы!