Некоторые обозначения

Логические знаки.

Математический текст состоит из математических формул и собственно текста, для которого используется русский (или какой-либо другой) язык. Некоторые словосочетания, которые выражают наиболее важные и часто используемые отношения между объектами, имеют специальные обозначения и называются логическими знаками. Наиболее употребительными являются следующие:

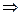– “влечет за собой”, “следует”;

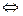– “тогда и только тогда”;

– “для всех”, “для каждого”;

– “существует”;

– “существует точно один”.

Нам нужно следующее обозначение суммы конечного числа слагаемых

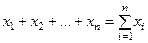(1)

В этом обозначении 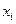называют общим членом суммы, 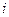-индексом суммирования, 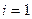и - нижним и верхним пределами суммирования.

Некоторые свойства суммирования

1) Индекс суммирования в (1) можно заменить другим:

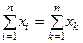
2) Множитель, не зависящий от индекса суммирования, можно выносить за знак суммы:

.

3) При двойном суммировании можно изменять порядок суммирования:

(2)

3) Определение матрицы. Примеры. Равенство двух матриц.

Определение 1. Матрицей размерности 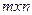называется прямоугольная таблица из 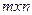чисел, расположенных в 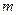строках и столбцах.

Обозначаются матрицы, как правило, большими буквами 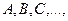или подробно

или

Например, матрицы

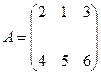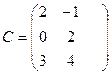, , и

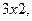
имеют, соответственно, размерности . Числа 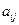, образующие матрицу, называются элементами матрицы. При этом первый индекс обозначает номер строки, а второй 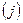- номер столбца, в которых расположен элемент 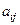. Так, 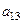- элемент первой строки и третьего столбца матрицы .

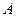Рассмотрим некоторые примеры матриц.

1) Квадратная матрица. Матрица размерности называется квадратной матрицей порядка . Общий вид квадратной матрицы

или .

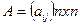Например, и 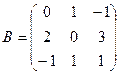есть квадратные матрицы второго и третьего порядков соответственно.

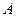Элементы (или ) квадратной матрицы называются диагональными элементами (или говорят, что они лежат на главной диагонали матрицы).

2) Матрица - строка. Это матрица размера :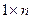

.

3) Матрица - столбец. Это матрица размера :

.

Замечание 1. Матрицу – строку часто называют просто строкой, а матрицу-столбец – просто столбцом. При этом для простоты записи элементы этих матриц снабжают только одним индексом. Иногда в обозначениях используют черту: снизу – для строки, сверху для столбца. Например, , .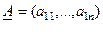

4) Треугольная матрица. Это квадратная матрица, у которой элементы, расположенные под диагональю (или над диагональю), равны нулю. Например, , , .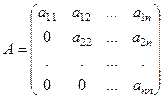

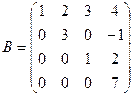5) Нулевая матрица. Это матрица, все элементы которой равны нулю. Нулевая матрица обозначается символом 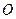. Если желают явно указать размерность матрицы, то пишут .

6) Единичная матрица. Квадратная матрица, все диагональные элементы которой равны 1, а остальные – нулю, называется единичной и обозначается 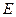или , где - ее порядок. Таким образом,

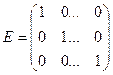
Определение 2. Две матрицы называются равными, если у них:

1) одинаковое число строк и столбцов, т.е. совпадают размерности матриц;

2) элементы, стоящие на соответственных местах этих матриц, равны.

Дата добавления: 2014-11-06