КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейная независимость строк и столбцов
|
|
|
|
Определение1. Линейной комбинацией столбцов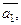 
…, 
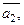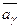одной размерности называется столбец 
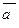вида
,
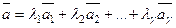где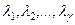 
- действительные числа, называемые коэффициентами линейной комбинации.
Определение 2. Система столбцов 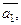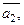…, 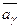называется линейно независимой, если
.
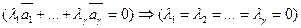В противном случае система столбцов 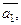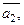…, 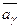называется линейно зависимой.
Пример 1. Если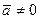 
, то система, состоящая из единственного столбца 
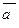, линейно независима.
Пример 2. Столбцы
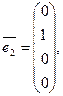
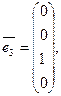
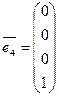
линейно независимы, так как
,
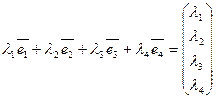и равенство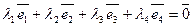 
возможно лишь в том случае, когда 
.
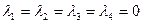Теорема 1(Свойства линейно зависимых и линейно независимых систем).
1) Система столбцов 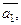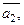…, 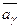линейно зависима 
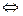один из этих столбцов есть линейная комбинация остальных.
2) Если среди столбцов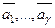 
есть нулевой, то они составляют линейно зависимую систему.
3) Если система столбцов содержит линейно зависимую подсистему, то вся система линейно зависима.
4) Если система столбцов линейно независима, то и любая ее подсистема линейно независима.
Аналогичным образом определяется линейная зависимость и линейная независимость строк.
Предложение1. Если в квадратной матрице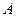 
какой-либо столбец (строка) является линейной комбинацией остальных столбцов (строк), то 
.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 311; Нарушение авторских прав?; Мы поможем в написании вашей работы!