Определители

Транспонирование матриц

Рассмотрим произвольную матрицу

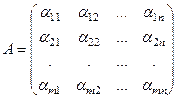
Определение 1. Матрица

,

пк нспонированнойолбцами, называется смысл, ассоциативно, т.е.

атриц не коммутативноет называться правилом умножения размерносолучающаяся из матрицы 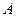заменой строк столбцами, называется транспонированной к .

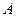Вместо 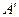иногда пишут .

Теорема 1(Правила транспонирования).

1) ;

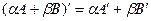2) .

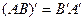Определение 1. Определителем матрицы 1-го порядка, образованной числом 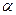, называется само это число 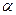. Пусть теперь для какого-то натурального числа 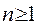мы уже знаем, какое число является определителем произвольной квадратной матрицы -го порядка. Тогда для произвольной квадратной матрицы 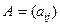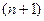-го порядка по определению полагаем:

1) минор элемента 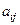матрицы 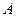есть определитель -го порядка, получаемый из определителя матрицы 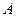вычеркиванием 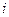-ой строки и -го столбца;

2) алгебраическое дополнение 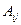элемента 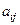есть ;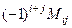

3) определитель 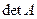матрицы 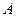равен .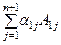

Согласно этому определению мы получаем следующие правила вычисления определителей второго и третьего порядка:

;

.

Следующая теорема устанавливает равноправие всех его столбцов и строк.

Теорема 1. Пусть 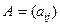есть произвольная квадратная матрица порядка . Тогда

Равенство называется разложением определителя по элементам 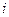- ой строки;

Равенство называется разложением определителя по элементам - го столбца.

Теорема 2 (Свойства определителя).

1) Общий множитель всех элементов какой-либо строки (или какого-либо столбца) можно выносить за знак определителя.

2) При перестановке двух строк (или столбцов) определитель меняет знак на противоположный.

3) Если к элементам некоторого столбца (или некоторой строки) определителя прибавить соответствующие элементы другого столбца (или другой строки), умноженные на общий множитель, то величина определителя при этом не измениться.

4) При транспонировании квадратной матрицы величина ее определителя не меняется.

5) Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю:

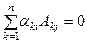
Следствие 1. Если определитель имеет две одинаковые строки или два одинаковых столбца, то он равен нулю.

Следствие 2. Если в определителе две строки или два столбца пропорциональны, то он равен нулю.

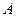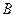Теорема 3. Пусть и - квадратные матрицы одного и того же порядка. Тогда

(определитель произведения матриц равен произведению определителей).

Дата добавления: 2014-11-06