Сигналы с обобщенной модуляцией

Энергетические характеристики сигналов УМ

Средняя мощность сигнала равна мощности несущей.

Сравнительные характеристики АМ и УМ сигналов
Параметр	АМ	ЧМ
Помехоустойчивость	–	+
Ширина спектра	+	–
Энергетические соотношения	–	+

Сигналы с обобщенной модуляцией – это сигналы с одновременным использованием амплитудно-модулированных и частотно-модулированных сигналов.

Анализ таких сигналов более сложен, но он упрощается, если использовать понятие комплексной огибающей сигнала.

Представим выражение

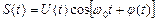
в виде комплексной величины:

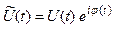- комплексная огибающая сигнала,

где 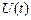- амплитуда, 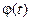- фаза,

т. е. 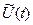содержит информацию о законах изменения амплитуды и фазового угла. Эта запись возможна только тогда, когда 1 изменяется намного медленнее, чем 2. Это достигается, если частота модулирующего сигнала намного меньше несущей частоты, т. е. понятие комплексной огибающей можно использовать только для узкополосных сигналов.

Введем понятие спектральной плотности комплексной огибающей:

.

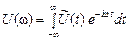Выразим спектральную плотность модулированного сигнала:

,

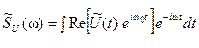в данной формуле выражение 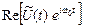описывает .

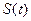Пусть 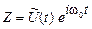, тогда

получим

.

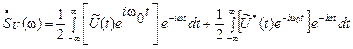В данной формуле первый интеграл - это 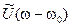, а второй - ,

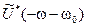получаем

.

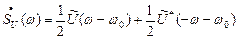Эта формула устанавливает связь между спектром модулированного сигнала и спектром его комплексной огибающей. Отсюда следует, что для определения спектра с обобщенной модуляцией достаточно найти спектральную плотность его комплексной огибающей и осуществить перенос ее из области частот 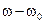в область частот 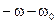. Причем при 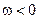выполняется также операция комплексного сопряжения.

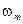- максимальная частота спектра комплексной огибающей. Если 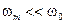(т. е. сигнал узкополосный), то тогда в области положительных частот можно использовать только первое слагаемое:

.

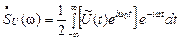Тогда ширина спектра модулированного сигнала равна

.

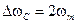Примером таких сигналов может служить радиолокационный сигнал с частотной модуляцией.

Дата добавления: 2014-11-06