Вероятностные характеристики случайных сигналов

Случайные сигналы

Тест № 2

Вопросы для самопроверки

1. Объясните причину возникновения искажений в передаче сообщений, наблюдаемых при перемодуляции.

2. Чем определяется распределение мощности в спектре АМ сигнала?

3. Почему непосредственная демодуляция ОБП сигнала приводит к искажению передаваемого сообщения?

4. Укажите сходства и различия между сигналами с частотной и фазовой модуляцией.

5. Как связаны между собой частота модуляции, ее индекс и девиация частоты?

6. Объясните различие между спектрами АМ и ЧМ сигналов.

7. Укажите особенности модуляции цифровых сигналов.

1. Модуляцией называется процесс:

a. Суммирования низкочастотного информационного сигнала и высокочастотного несущего колебания;

b. Изменения одного из параметров высокочастотного колебания под воздействием низкочастотного сигнала, отображающего передаваемое сообщение;

c. Перемножения низкочастотного информационного сигнала и высокочастотного несущего колебания;

d. Выделения модуля комплексного сигнала.

2. Амплитудной модуляцией называется процесс изменения амплитуды:

a. Сигнала при изменении его фазы;

b. Сигнала при изменении его частоты;

c. Сигнала при его прохождении через линейный четырехполюсник;

d. Высокочастотного несущего колебания по закону передаваемого сообщения.

3. Частотной модуляцией называется процесс изменения частоты:

a. Сигнала при изменении его фазы;

b. Сигнала при изменении его амплитуды;

c. Высокочастотного несущего колебания по закону передаваемого сообщения;

d. Сигнала при его прохождении через нелинейный четырехполюсник.

4. Фазовой модуляцией называется процесс изменения фазы:

a. Сигнала при изменении его частоты;

b. Сигнала при изменении его амплитуды;

c. Высокочастотного несущего колебания по закону передаваемого сообщения;

d. Сигнала при его прохождении через нелинейный четырехполюсник.

5. Спектр амплитудно-модулированного сигнала состоит из:

a. Частоты несущего колебания и двух боковых полос;

b. Частоты несущего колебания и одной боковой полосы;

c. Частоты несущего колебания и кратных частот;

d. Только из боковых полос.

Случайный процесс (СП) – совокупность (ансамбль) функций времени, подчиняющийся некоторой общей для них статистической закономерности. Бывают непрерывные, дискретные, квантованные и цифровые СП.

Если взять конкретные значения t ₁, то, усреднив их, можно получить математическое ожидание.

,

.

F(x) – интегральный закон распределения. Он показывает вероятность того, что произвольно взятое Х будет меньше х.

Плотность распределения величины показывает, какова наибольшая вероятность попадания в заданный интервал.

На практике наиболее значимыми являются следующие параметры СП.

Математическое ожидание – величина, к которой в среднем стремится СП:

.

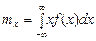Дисперсия характеризует мощность процесса, разброс случайных значений относительно математического ожидания

.

Среднеквадратическое отклонение характеризует линейный разброс, а не квадратичный, как дисперсия:

.

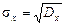Для дискретных сигналов каждое значение возможно с вероятностью р _к, но .

Свойства

1. Если х ₁> х ₂, то F(x₁)>F(x₂).

2. F (-¥)=0, F (+¥)=1.

3. Если х ® -¥ (х ® +¥), то f(x)®0.

4. –– площадь плотности вероятности всегда равна 1.

Дата добавления: 2014-11-06