Частотные и временные характеристики линейных цепей

Линейные цепи

Тест № 3

Вопросы для самопроверки

1. Перечислите основные свойства плотности вероятности случайной величины.

2. Как связаны между собой плотность вероятности и характеристическая функция случайной величины?

3. Перечислите основные законы распределения случайной величины.

4. Каков физический смысл дисперсии эргодического случайного процесса?

5. Приведите несколько примеров линейных и нелинейных, стационарных и нестационарных систем.

1. Случайным процессом называется:

a. Любое случайное изменение некоторой физической величины во времени;

b. Совокупность функций времени, подчиняющихся некоторой общей для них статистической закономерности;

c. Совокупность случайных чисел, подчиняющихся некоторой общей для них статистической закономерности;

d. Совокупность случайных функций времени.

2. Стационарность случайного процесса означает, что на протяжении всего отрезка времени:

a. Математическое ожидание и дисперсия неизменны, а автокорреляционная функция зависит только от разности значений времени t ₁ и t ₂;

b. Математическое ожидание и дисперсия неизменны, а автокорреляционная функция зависит только от моментов времени начала и конца процесса;

c. Математическое ожидание неизменно, а дисперсия зависит только от разности значений времени t ₁ и t ₂;

d. Дисперсия неизменна, а математическое ожидание зависит только от времени начала и конца процесса.

3. Эргодический процесс означает, что параметры случайного процесса можно определить по:

a. Нескольким конечным реализациям;

b. Одной конечной реализации;

c Одной бесконечной реализации;

d. Нескольким бесконечным реализациям.

4. Спектральная плотность мощности эргодического процесса - это:

a. Предел спектральной плотности усеченной реализации, деленной на время Т;

b. Спектральная плотность конечной реализации длительностью T, деленная на время Т;

c. Предел спектральной плотности усеченной реализации;

d. Спектральная плотность конечной реализации длительностью T.

5. Теорема Винера – Хинчина есть соотношение между:

a. Энергетическим спектром и математическим ожиданием случайного процесса;

b. Энергетическим спектром и дисперсией случайного процесса;

c. Корреляционной функцией и дисперсией случайного процесса;

d. Энергетическим спектром и корреляционной функцией случайного процесса.

Электрическая цепь осуществляет преобразование сигналов, поступающих на ее вход. Поэтому в самом общем случае математическую модель цепи можно задать в виде соотношения между входным воздействием S_вх(t) и выходной реакцией S_вых(t):

S_вых(t)=TS_вх(t),

где Т – оператор цепи.

На основании фундаментальных свойств оператора можно сделать заключение о наиболее существенных свойствах цепей.

1. Если оператор цепи Т не зависит от амплитуды воздействия, то цепь называется линейной. Для такой цепи справедлив принцип суперпозиции, отражающей независимость действия нескольких входных воздействий:

T[S_вх1(t)+ S_вх2(t)+…+ S_вхn(t)]=TS_вх1(t)+TS_вх2(t)+…+TS_вхn(t).

Очевидно, что при линейном преобразовании сигналов в спектре отклика нет колебаний с частотами, отличными от частот спектра воздействий.

Класс линейных цепей образуют как пассивные цепи, состоящие из резисторов, конденсаторов, индуктивностей, так и активные цепи, включающие еще и транзисторы, лампы и т. п. Но в любой комбинации этих элементов их параметры не должны зависеть от амплитуды воздействия.

2. Если сдвиг входного сигнала во времени приводит к такому же сдвигу выходного сигнала, т. е.

S_вых(t 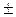t₀)=TS_вх(t 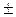t₀),

то цепь называют стационарной. Свойство стационарности не распространяется на цепи, содержащие элементы с переменными во времени параметрами (индуктивности, конденсаторы и т. п.).

Дата добавления: 2014-11-06