Дельта-функция как пример пробного сигнала

Для анализа прохождения сигналов через электрические цепи широко используются пробные сигналы, обладающие какими - либо характерными свойствами. Такой функцией, в частности, является дельта-функция d (t), обращающаяся в ноль при t¹ 0 и в бесконечность при t= 0 так, что

.

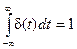Этому определению удовлетворяет, например, прямоугольный импульс длительностью t _u , амплитуда которого обратно пропорциональна его длительности 1/ t _u . При t _u®0 амплитуда импульса бесконечно растет, а площадь остается постоянной – равной единице. Действительно, если

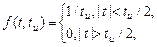
то дельта-функцию можно определить как d(t)= .

При этом

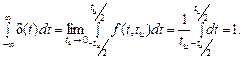
В более общем случае дельта-функцию можно записать в виде

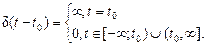
Спектральную плотность дельта-импульса A d(t) найдем с помощью прямого преобразования Фурье:

.

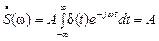На основании определения дельта-функции интервал интегрирования в формуле можно сделать сколь угодно малым, лишь бы он включал в себя момент t= 0. В пределе он может быть устремлен к нулю и подынтегральная функция e^jwt примет значение, равное единице. Таким образом, . Следовательно, спектральная плотность дельта-импульса имеет равномерный частотный спектр. ФЧХ дельта-импульса равна нулю для всех частот. Это означает, что все гармонические составляющие начинаются с одной фазы и образуют бесконечный пик при t= 0.

По определению, дельта-функция обладает свойством, которое может быть выражено соотношением

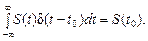
Его называют фильтрующим свойством дельта-функции, согласно которому интеграл от произведения произвольной функции на d (t-t₀) равен значению этой функции в точке t=t₀ .

На основании обратного преобразования Фурье выразим дельта-функцию через ее спектр:

d (t)= .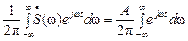

По аналогии можно ввести дельта-функцию аргумента w:

d(w)= .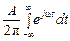

Знак показателя экспоненты не влияет на значение интеграла, поскольку 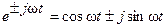, и независимо от знака интеграл от нечетной функции sin на симметричном интервале интегрирования равен нулю. Поэтому можно записать:

d(w)= .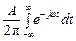

Дата добавления: 2014-11-06