Случайных сигналов

Корреляционный и спектральный анализы

Спектральная плотность сигнала может быть определена только для постоянного процесса. Для случайного процесса это невозможно, поэтому используют спектральную плотность мощности.

Пусть имеется k -я реализация случайного процесса Х_К(t). Ограничим ее отрезком времени Т. Теперь это усеченная k -я реализация Х_КТ(t). Найдем спектральную плотность Х_КТ (w) для Х_КТ(t). Отсюда энергия на рассматриваемом участке по равенству Парсеваля:

.

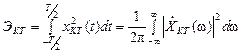Получим среднюю мощность реализации на отрезке Т, поделив выражение на Т:

.

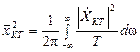При увеличении Т энергия возрастает, но отношение Э_КТ / Т остается постоянным.

.

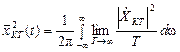Отсюда 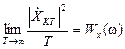–– спектральная плотность мощности. Это предел спектральной плотности усеченной реализации, деленной на время Т. Это запись для эргодического процесса.

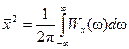–– среднее значение квадрата процесса.

Если 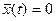, то .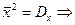

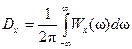Теорема Винера – Хинчина

Это есть соотношение между энергетическим спектром и корреляционной функцией случайного процесса.

,

.

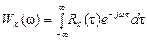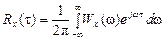Это прямое и обратное преобразования Фурье соответственно.

При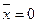

,

.

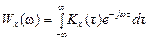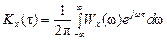Выводы

1.	Случайный процесс (СП) – совокупность (ансамбль) функций времени, подчиняющийся некоторой общей для них статистической закономерности. Бывают непрерывные, дискретные, квантованные и цифровые СП.
2.	Математическое ожидание – величина, к которой в среднем стремится СП.
3.	Дисперсия характеризует мощность процесса, разброс слу-чайных значений относительно математического ожидания.
4.	Среднеквадратическое отклонение характеризует линейный разброс, а не квадратичный, как дисперсия.
5.	Ковариационная функция характеризует взаимодействие случайного процесса между собой в случайные моменты времени t1 и t2.
6.	Стационарность в широком смысле понимается так: на протяжении всего отрезка времени математическое ожидание и дисперсия неизменны, а автокорреляционная функция зависит только от разности значений времени t1 и t2 и не зависит от времени начала и конца процесса.
7.	Эргодический процесс – это такой процесс, при котором па-раметры случайного процесса можно определить по одной бесконечной реализации.
8.	Независимые процессы всегда некоррелированные, зависимые процессы могут быть как коррелированными, так и некоррелированными.
9.	Теорема Винера-Хинчина определяет соотношение между энергетическим спектром и корреляционной функцией случайного процесса.
10.	Энергетический спектр и корреляционная функция связаны между собой прямым и обратным преобразованиями Фурье.

Дата добавления: 2014-11-06