Прямоугольных импульсов

Амплитудно-манипулированный сигнал

Спектры манипулированных сигналов

,

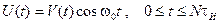где 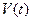- огибающая,

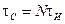- длительность всего сигнала. Для рассмотренных выше случаев N =4.

N = 4

Огибающая повторяет модулирующий сигнал:

.

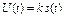Далее, пользуясь преобразованиями Фурье, получим

,

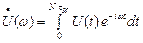тогда спектр сигнала можно выразить через формулу

,

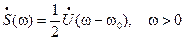т. е. спектр огибающей – это спектр цифрового сигнала.

t

Спектральная плотность последовательности

Спектральная плотность прямоугольного импульса равна .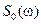

,

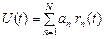где a_n – кодовая комбинация,

{ a_n } = a₁, a₂, a₃, a₄… a_N,

при этом a_N равно 1 или 0, длина равна N элементам,

r_n(t) описывает прямоугольный импульс:

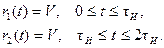
Через преобразование Фурье

,

,

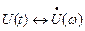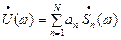где 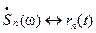- спектр прямоугольного импульса,

,

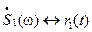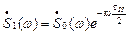- теорема об импульсах.

.

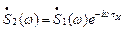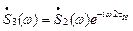и т. д.,

отсюда получим

,

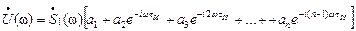эту формулу можно переписать в компактном виде:

,

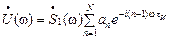где 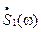- спектральная плотность первого импульса.

Тогда спектр кодовой последовательности запишется так:

.

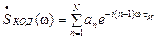Из этого выражения видно, что спектр кодовой последовательности 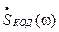является периодическим спектром с периодом на оси частот, равным .

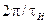Спектр огибающей (цифрового сигнала) запишется так:

,

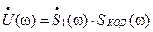отсюда следует, что спектр огибающей (цифрового сигнала) является результатом наложения на спектр обычного прямоугольного импульса 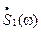спектра кодовой последовательности .

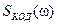На графике показан примерный вид .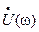

Жирной плавной линией показан спектр одиночного импульса.

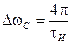- практическая ширина спектра при Амн. 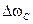- один из наиболее важных параметров.

ВЫВОД. 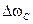зависит от длины импульса.

Для фазовой модуляции (ФМн) почти все выкладки, приведенные выше, идентичны. Наиболее важно то, что при ФМн ширина спектра будет такая же:

.

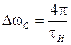Построим спектр частотно-манипулированного (ЧМн) сигнала.

Для упрощения возьмем длину кодовой последовательности N, равную 2. График модулированной последовательности (0 и 1) показан ниже.

.

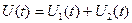Данный график можно представить в виде двух отдельных графиков:

А их спектры выглядят так.

Если сложить эти два спектра, график будет иметь приблизительно такой вид:

.

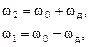
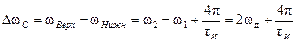Из данной формулы видно, что ширина спектра при частотно-манипулированном (ЧМн) сигнале зависит еще и от девиации частоты.

ВЫВОД. При любом виде манипуляций ширина спектра манипулированного сигнала обратно пропорциональна длительности импульса (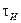). При передаче цифрового сигнала 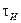- это длительность посылки одного символа двоичного кода, а частоту

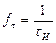
называют тактовой частотой. С ней связано такое понятие, как скорость передачи цифровой информации (число переданных двоичных символов – бит за 1 секунду). Например, 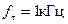, это означает, что скорость передачи двоичных символов равна 1000 б/с или 1 кб/с. То есть за одну секунду передаются 1000 двоичных символов. Следовательно, чем меньше длительность единичного элемента манипулированного сигнала, тем выше скорость передачи цифровой информации. Однако увеличение скорости передачи цифровой информации приводит к расширению спектра. Основной недостаток манипулированных сигналов – требования к ширине полосы пропускания. И чем выше скорость передачи, тем шире полоса пропускания.

Дата добавления: 2014-11-06