Z-преобразование

Это преобразование можно получить из преобразования Лапласа или Фурье для дискретного сигнала x_g (t).

Определим одностороннее преобразование Лапласа (для сигналов, определенных при t≥ 0 для дискретного сигнала вида (11.1)):

При p = jω из (11.31) следует преобразование Фурье для дискретного сигнала.

Если обозначить:

то преобразование Лапласа (11.31) переходит в Z- преобразование дискретного сигнала X _g(t):

Очевидно, что из преобразования Фурье дискретного сигнала X _g(t)

следует также Z-преобразование X (z),

Справедливо и обратное утверждение: из Z-преобразования X (z) дискретного сигнала (11.33) при 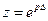следует преобразование Лапласа. Или из X (z) при 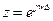следует преобразование Фурье сигнала.

Если дискретный сигнал X _g(t) определен и при t <0, то вместо (11.33) можно ввести более общее преобразование для такого сигнала:

Следует оговорить сходимость X (z) при неограниченном числе слагаемых в (11.33) или (11.35). Отсчеты x (k) всегда удовлетворяют условию | x (k)|< CR^k, k > 0, C >0 и R >0 - постоянные вещественные числа. Тогда (11.33) сходится при всех Z, для которых │ z │> R (т. е. в кольцевой области с радиусом сходимости R). В области сходимости X (z) представляет собой аналитическую функцию переменной z, не имеющую в этой области ни полюсов, ни существенно особых точек.

Для нахождения x (k) по X (z) (т. е. обратного Z-преобразования) умножим левую и правую части (11.33) на Z^{n -1:}

Возьмем от левой и правой частей (11.36) интеграл по z по замкнутому контуру в области аналитичности, охватывающей все полюсы функции X (z) z ^n-1. Получим следующий результат:

Этот результат следует из теоремы Коши при интегрировании функции комплексного переменного z:

Наиболее важное свойство Z-преобразования связано со сдвигом сигнала во времени:

Таким образом, Z-преобразование дискретного сигнала y (t), у которого все отсчеты смещены на один такт в сторону запаздывания относительно дискретного сигнала X _g(t), равно произведению z ^-1 на X (z). Можно сказать, что z ^-1 является оператором сдвига на один

такт в сторону запаздывания. Для доказательства (11.39) запишем Z-преобразование последовательности{ y (k)= x (k -1)}:

Вводя переменную k -1= n, из (11.40) получим (11.39). Очевидно, если

y (k)= x (k-n), то Y (z)= z ^--n X (z).

Рассмотрим дискретную свертку конечной протяженности :

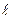Найдем Z-преобразование этой свертки:

таким образом, свертка двух дискретных сигналов соответствует произведению их Z-преобразований.

Покажем, что импульсная характеристика ЦФ { g (0), g (1)… g (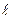)} является его откликом на единичный импульс (1,0,0,0,0,…). Действительно, при воздействии единичного импульса формула (11.41) принимает вид

y (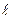)= g (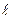), 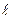=0,1,2… (11.43)

Если импульсная характеристика ЦФ финитна, то

y (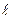)=0 при 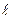=L+1, (11.44)

где (L +1)- число тактовых отрезков на интервале финитности.

Рассмотрим прохождение через линейный ЦФ гармонической последовательности вида x (t)= e^{j (ω t +φ)} или в дискретном виде

x (k)= e^{j (ωkΔ+φ)} . (11.45)

Согласно формуле свертки (11.41) с учетом (11.45) находим выходной сигнал:

Введем над знаком суммы новый индекс суммирования l-k=n и учтем, что из соображений реализуемости g (n)=0 при n <0. Тогда

где

- комплексная передаточная характеристика ЦФ. Импульсная характеристика ЦФ в реальном масштабе времени будет иметь вид

причем Ќцф (f) является преобразованием Фурье от дискретного сигнала вида (11.48).

Как следует из (11.47), Ќцф (f) является периодической функцией частоты дискретизации F _g=1/Δ (как и спектр дискретного сигнала).

Если в (11.47) ввести переменную z = e^{j ωΔ}, то получим Z-преобразование импульсной характеристики ЦФ:

H (z) называют системной функцией стационарного линейного ЦФ.

Из (11.42) при замене G (z) на H (z) видно, что системная функция ЦФ определяется как отношение Z-преобразования выходного сигнала фильтра к Z-преобразованию входного сигнала:

Если в системной функции ЦФ положить 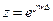, получим частотную характеристику ЦФ:

Таким образом, применение Z-преобразований позволяет проводить анализ цифровых фильтров теми же методами, что и анализ аналоговых линейных цепей.

Дата добавления: 2014-11-06