Алгоритм быстрого преобразования Фурье

Преобразования Фурье и метода Z-преобразования в анализе дискретных фильтров

Использование дискретного

При вычислении N коэффициентов ДПФ согласно (11.8) или ОДПФ согласно (11.11) надо выполнить N ² достаточно трудоемких операций умножения. При больших массивах N (порядок 10³ и выше) использование (11.8) и (11.11) в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств. Задача существенно упрощается с применением алгоритмов быстрого преобразования Фурье (БПФ), которые сводят обработку заданного массива данных к обработке массивов с меньшим числом членов, и тем самым существенно уменьшается требуемое число операций умножения.

Сущность одного из алгоритмов БПФ для вычисления коэффициентов Ćn для массива вещественных данных { x (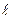)}, объема N =2^r, где r - целое число, состоит в следующем.

Разобьем исходный массив данных { x (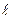)} на две части с четными и нечетными номерами:

Согласно (11.8) коэффициенты N·Ćn на первом этапе разбиения равны

Из (11.12) следует, что последовательности коэффициентов Ć ¹ nчет и Ć ¹ nнеч обладают свойством периодичности с периодом N /2:

Кроме того, для n > N /2 множитель в (11.12) можно предста

вить в виде

С учетом (12), (13) и (14) для всех n =0,1,2,3… N -1 можно записать:

Причем знак "-" соответствует значениям n = N /2, N /2+1,… N -1. Подсчитаем, сколько требуется операций умножения при вычислении всех значений ĆnN по алгоритму (11.15). Для вычисления всех Ć¹nчет по (11.12) требуется (N /2)² умножений. Столько же умножений требуется для вычисления всех Ć¹nнеч. Кроме того, потребуется N умножений Ć¹nнеч на число + . Следовательно, потребуется 2(N /2)²+ N умножений. При больших N требуемое число умножений равно N ²/2= N log2 N (при N =4), что в 2 раза меньше, чем по алгоритму (11.8).

Четные отсчеты исходной последовательности Х ¹ чет (k) (их всего N /2) разобьем далее на втором этапе разбиения на четные и нечетные компоненты x "(2 k) и x "(2 k +1) (их число равно N /4). ДПФ последних обозначим Ć"nчет и Ć"nнеч. Тогда можно написать:

Аналогичное разбиение выполняется над нечетными отсчетами исходной последовательности Х¹неч(k). Для вычисления всех ĆnN согласно формулам типа (11.16) (по массиву данных)

потребуется число умножений (при N =8).

Процесс разбиений можно продолжать r раз до тех пор, пока не получится последовательность из одного элемента, ДПФ которого совпадает с самим элементом. Далее надо собрать результаты отдельных разбиений для вычисления суммарных значений ĆnN. Анализ показывает, что число операций умножения, необходимых для вычисления БПФ, не больше, чем Nr = N log₂ N, что при больших N существенно меньше, чем N ². БПФ по рассматриваемому методу осуществляют в следующем порядке. Сначала для получения желательного при обработке сигнала порядке следования отсчетов x (k), k =0,1,2,…, N -1 выполняется двоично-инверсная перестановка исходной последовательности x (q), q =0,1,…, N -1. Для этого записывают порядковые номера элементов x (q) в двоичном коде и инвертируют порядок следования разрядов. Новый порядок следования элементов x (k) определяется номерами, получаемыми после инверсии разрядов.

Пример для N =4

x(q)		x(k)
0→	00→	00→	0→
1→	01→	10→	2→
2→	10→	01→	1→
3→	11→	11→	3→

Новый порядок следования элементов следующий: x (0), x (2), x (1), x (3). После этого поступают так: на первом этапе вычислений определяют 2 - точечные элементы ДПФ "новой" последовательности x (k), объединяя попарно элементы этой последовательности; на втором этапе из 2 - точечных ДПФ получают 4 - точечные ДПФ, пользуясь основной операцией данного метода (об этом ниже); затем 4- точечные ДПФ объединяются в 8 - точечные и т. д.

Базовые операции показывают, как два входных числа A и B объединяются для получения двух выходных чисел X и Y. Для метода прореживания во времени базовая операция имеет вид:

- в графическом виде

Операция "бабочка", используемая при реализации алгоритма БПФ (стрелка означает умножение на B).

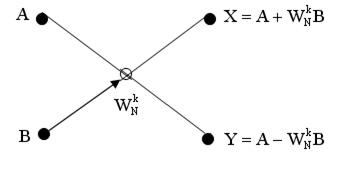
Граф для вычисления БПФ при N =4

-или в форме уравнений

При вычислении двухточечного ДПФ k=0 и выходные числа X и Y определяются без операции умножения X = A + B, Y = A - B.

Чтобы воспользоваться рассмотренной процедурой БДПФ для вычисления ОДПФ, запишем (11.11) в виде

*) – комплексно-сопряженные числа.

Вводя массив данных C вместо x (n), можно найти сумму в (11.18) по изложенной выше методике БДПФ, затем для нахождения x (k) найти комплексно-сопряженное значение полученного результата.

Существуют и другие методы вычисления БДПФ, т. е. другие методы группирования исходных данных x (k).

Подобно тому, как отклик аналоговой линейной стационарной системы y (t) на произвольное внешнее воздействие x (t) можно найти временным методом через импульсную характеристику системы g (t):

или спектральным методом через комплексный коэффициент k (w)

передачи цепи, так и отклик линейного стационарного цифрового фильтра y (n) на произвольное внешнее воздействие x (n) можно найти через импульсную характеристику ЦФ g (n) или спектральным методом.

Выполнив в (11.19) дискретизацию по переменным τ и t, положив τ= k Δ, t = m Δ, получаем цифровой аналог свертки (11.19):

где g (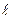), 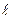=0,1,2,…, L – отсчеты импульсной характеристики ЦФ, т. е. отклика на единичный импульс (1,0,0,0,0,0,…), поступающий на вход фильтра в момент времени t =0. Из условий реализуемости ЦФ надо принять:

g (- )=0, 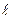=1,2… (11.21)

Если входные отсчеты x (k) начинают поступать в момент t =0, то можно написать:

Из условия реализуемости ЦФ (11.21) следует, что суммирование в (11.22) фактически выполняется только при k≤m:

Если число входных отсчетов x (0), x (1),…, x (N -1) равно N, а число отсчетов импульсной характеристики ЦФ (g (0), g (1),…, x (L)) равно (L +1), то в (11.23) m принимает значения 0,1,2,…, N _Σ-1 (N _Σ= N + L). Для нахождения одного значения y (m) в соответствии с (11.23) надо выполнить не более чем (L +1) операций умножения. Для нахождения всех значений y (m) надо выполнить примерно операций умножения.

Число операций можно существенно сократить, если использовать спектральный метод расчета ЦФ и методы БПФ. Чтобы это показать, напишем сначала дискретную свертку (11.23) в нормированном виде:

Дополнив последовательность из N входных отсчетов x (k) L нулями, представим x (k) через ОДПФ.

Дополнив последовательность из (Q +1) отсчетов импульсной характеристикой ЦФ (N +1) нулями, определим ОДПФ:

где - коэффициенты ДПФ для импульсной характеристики ЦФ.

Подставляя (11.25) и (11.26) в (11.24), получаем

Справедливо условие

Равенство суммы N при n = 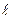очевидно. Равенство же суммы нулю при n≠ 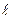объясняется тем, что в этом случае имеем сумму единичных векторов, образующих в совокупности правильный N -угольник. Сумма эта, естественно, равна нулю.

С учетом (11.28) формула (11.27) принимает вид

Уравнение (11.29) определяет ОДПФ выходных отсчетов ЦФ, если ДПФ над этими отсчетами определяется произведением ДПФ входных отсчетов и отсчетов импульсной характеристики фильтра:

Если методами БПФ найти спектральные компоненты 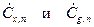, а затем и ОДПФ от их произведения C_yn = C_xnC_gn, то можно при больших N существенно cэкономить в вычислительных операциях по сравнению с непосредственными вычислениями y (m) по формуле дискретной свертки.

Дата добавления: 2014-11-06