Основы реализации цифровых фильтров

В общем случае в линейном стационарном цифровом фильтре k -й выходной отсчет y (k) (в момент времени t = k Δ) линейно зависит от k -го входного отсчета x (k) и некоторого количества предшествующих отсчетов x (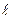) ( 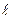< k), а также от некоторого количества
выходных отсчетов y (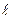) ( 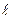< k):

Числа L и M в разностном уравнении (11.52) называют соответственно относительной памятью ЦФ по входу и выходу. ЦФ с памятью по выходу называются рекурсивными, а без такой памяти нерекурсивными.

Алгоритмы работы различных ЦФ отличаются параметрами L и M и набором коэффициентов { a_ℓ } и { bi }. Рассмотрим сначала реализацию нерекурсивных ЦФ, когда все b_i =0 (т. е. М =0).

В этом случае разностное уравнение (11.52) принимает вид

Структурная схема ЦФ, реализующая алгоритм (11.53), приведена на следующем рисунке.

Структурная схема построения нерекурсивного

(трансверсального) ЦФ

Основными элементами ЦФ являются блоки задержки отсчетных значений на один тактовый интервал (условно обозначены символом z ^-1), а также масштабные блоки a_q (усилители). Сигналы с последних собираются в сумматор, образуя выходной отсчет. Посредством разностного уравнения (11.53) можно построить лишь ЦФ с финитной (конечной) импульсной характеристикой { g (0), g (1)… g (Q)}. Если на вход схемы трансверсального типа подать единичный импульс (1,0,0,0,…), то по определению отклик ЦФ есть его импульсная характеристика g (t). Это возможно лишь при условии, что в трансверсальном ЦФ отсчеты импульсной характеристики g (q) совпадают с коэффициентами a_ℓ, ℓ =0,1,2,… Q.

Взяв Z-преобразование от левой и правой частей (11.53), получаем

Тогда системная функция трансверсального фильтра будет иметь вид

Равенство (11.54) определяет дробно-рациональную функцию от Z. Она имеет L -кратный полюс при Z =0 и L нулей, определяемых корнями полинома числителя формулы (11.54). Последние зависят от отсчетов импульсной характеристики

ЦФ g (ℓ)= a_ℓ. Частотная характеристика трансверсального цифрового фильтра согласно (11.54) и (11.51) имеет вид

Рассмотрим теперь работу ЦФ, работающего по общему алгоритму (11.52).

Структурная схема построения рекурсивного ЦФ

Взяв Z-преобразование от левой и правой частей (11.52), получим

Отсюда следует выражение для системной функции цифрового рекурсивного фильтра:

В реализуемых цифровых фильтрах обычно M > Q. При таких условиях дробно-рациональная функция (11.56) имеет на Z-плоскости L нулей, определяемых корнями Z_oi уравнения

где M-L -кратный ноль в точке Z =0;

М - числополюсов, определяемых корнями Z_ni уравнения

Если коэффициенты b_ℓ (ℓ =1, M) вещественны, то корни уравнения (11.57) (т. е. полюсы H (z)) лежат либо на вещественной оси, либо образуют комплексно - сопряженные пары.

Системной функции (11.56) соответствует частотная характеристика ЦФ:

где R_o,i = e^{j ωΔ}- z _o,i, R _{п ,i} = e^{j ωΔ}- z _{п ,i}.

АЧХ фильтра (в децибелах) определяется формулой

За счет наличия обратной связи рекурсивные ЦФ характеризуются нефинитной (длящейся неограниченно) импульсной характеристикой (откликом на единичный импульс 1,0,0,0,…).

Система с обратной связью нуждается в исследовании на устойчивость. ЦФ устойчив, если │ y_n │при n →∞ не превышает некоторого положительного числа А, независимо от выбора начальных условий в схеме. Чтобы исследовать устойчивость схемы, надо исследовать поведение свободных колебаний, т. е. уравнение (11.52) при отсутствии внешнего воздействия

Известно, что отдельное свободное колебание в линейной стационарной системе определяется выражением .При t = k Δ имеем . Обозначив , решение уравнения (11.58) можно искать в виде

Подставляя (11.59) в (11.58), получаем характеристическое уравнение, определяющее λ:

Уравнение (11.60) совпадает с уравнением (11.57), которому удовлетворяют полюсы системной функции рекурсивного ЦФ (классический алгебраический критерий устойчивости Раусса-Гурвица).

П ри найденных корнях уравнения (11.60) или (11.57) λ k = zk, k =1,…, M, общее решение уравнения (11.58) можно представить в виде

где ограниченные коэффициенты А 1, А 2, … Аm определяются начальными условиями.

Для момента времен с номером (k+1) из (11.61) следует

Если все полюса системной функции (11.56) удовлетворяют условию

т. е. они лежат внутри единичного круга с центром в точке z=0, то на основании (11.61) и (11.62) можно прийти к заключению, что все свободные колебания во времени определяются членами бесконечно убывающей геометрической прогрессии и фильтр будет устойчивым.

Недостатком рассмотренной схемы рекурсивного ЦФ является наличие отдельных элементов задержки для входных и выходных отсчетов.

Этот недостаток устранен в так называемой канонической схеме рекурсивного ЦФ, использующего общие элементы задержки для входных и выходных отсчетов, при M=L.

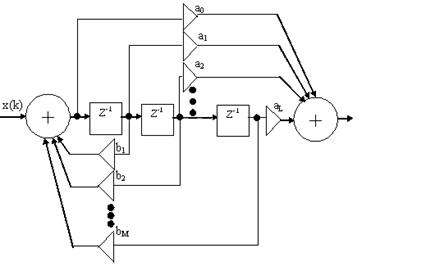
Каноническая схема реализации рекурсивного ЦФ

Каноническая схема идентична ранее рассмотренной схеме рекурсивного ЦФ. Чтобы это доказать, определим системную функцию ЦФ по канонической схеме. Обозначим значения дискретного отсчета в k-й момент времени на выходе первого сумматора через W (k). Согласно схеме очевидна справедливость уравнения

Дискретный сигнал на выходе второго сумматора в k-й момент времени

Выполним Z-преобразование над правой и левой частями (11.64-11.65). Получим

Приравняв значения W (z) из (11.66) и (11.67), имеем

Полученный результат не отличается от (11.56), что доказывает идентичность полной и канонической схем рекурсивного ЦФ.

Выводы

1.	Спектр дискретного сигнала повторяется с периодом частоты дискретизации F д.
2.	Коэффициенты ДПФ, номера которых располагаются симметрично относительно N /2, образуют комплексно-сопряженные пары.
3.	Z-преобразование дискретного сигнала y (t), у которого все отсчеты смещены на один такт в сторону запаздывания относительно дискретного сигнала X g(t), равно произведению z ^-1 на X (z).
4.	z ^-1 является оператором сдвига на один такт в сторону запаздывания.
5.	Свертка двух дискретных сигналов соответствует произведению их Z-преобразований.
6.	Применение Z-преобразований позволяет проводить анализ цифровых фильтров теми же методами, что и анализ аналоговых линейных цепей.

Дата добавления: 2014-11-06