Учет погрешности цифровой фильтрации из-за квантования сигнала по уровням

Появление быстродействующих многоразрядных процессоров цифровой обработки сигналов самых различных типов сделало возможным производить цифровую обработку сигналов не только речи и вещания, но и телевидения. Однако даже при такой совершенной технике необходимо учитывать погрешности работы ЦФ, обусловленные квантованием уровней сигналов.

Пусть х _max и x _min – наибольшее и наименьшее значения уровня сигнала на выходе аналого-цифрового преобразователя (АЦП). Если для квантования сигналов используется Q уровней, то при равномерном квантовании шаг квантования определяется соотношением

Квантованные отсчеты х _кв(k) описывают мгновенные значения аналогового дискретного сигнала x (k) с определенной погрешностью (с шумом квантования): ε(k)= x _кв(k)- x (k). Эта погрешность уменьшается (по модулю) с уменьшением Δ х. Будем считать, что квантователь работает по следующим правилам: в качестве дискретного принимается уровень, ближайший к истинному. Если действительный входной уровень x (k) находится в середине между дискретными номерами q и (q +1), выбирается любой из них. При оговоренных условиях погрешность ε_вх(k) лежит в пределах

Чаще всего считается, что случайная погрешность ε_вх (при различных k) равномерно распределена на отрезке

Тогда ее математическое ожидание (МО) равно нулю, а дисперсия

.

Определим погрешность работы линейного стационарного фильтра, обусловленную шумом квантования ε_вх(k). Дискретный входной отсчет ЦФ, обусловленный шумом квантования ε_вх(k) согласно (11.41) равен

Математическое ожидание выходного шума E _вых=0. Для нахождения дисперсии выходного шума 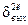предположим, что отдельные отсчеты входного шума E _вх(k) – независимые случайные величины с равномерным распределением и дисперсией

.

Тогда

.

.

Выходной шум ЦФ, обусловленный квантованием сигнала, тем меньше, чем быстрее убывают отсчеты импульсной характеристики фильтра. Относительную погрешность ЦФ, обусловленную шумом квантования, можно определить так:

Оценим влияние шума квантования на работу цифрового перемножителя. Из-за шума квантования квантованные отсчеты входного и опорного сигналов можно записать в виде

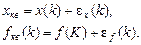
Схема цифрового

перемножителя

Тогда

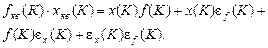
Ошибка цифрового перемножителя из-за шума квантования будет такой:

E_вых(k)=x(k)E_f(k)+f(k)E_x(x)+E_x(k)E_f(k).

При сделанных ранее предположениях о шуме квантования математическое ожидание 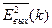. Предполагая шумы квантования сигналов x (t) и f (t) независимыми стационарными случайными процессами, получаем для дисперсии выходного шума перемножителя следующее выражение:

Если сигналы x (t) и f (t) квантуются с одинаковым шагом Δ_x=Δ_t= p, то

Относительная погрешность работы цифрового перемножителя, обусловленная шумом квантования, будет такой:

Выводы

1.	Устройства ЦОС обладают рядом преимуществ перед устройствами обработки сигналов в непрерывном времени и широко применяются на практике в системах передачи как дискретных, так и непрерывных сообщений.
2.	Наиболее широко применяются в системах связи линейные стационарные фильтры и перемножители.
3.	Спектр Фурье дискретного сигнала является периодической функцией частоты дискретизации.
4.	Линейчатый спектр дискретного (периодического) сигнала с числом отсчетов N определяется дискретным преобразованием Фурье (ДПФ). Число компонентов такого спектра Ćn равно N, а число амплитуд – N /2. По спектральным компонентам Ćn дискретные отсчеты x (k) определяются через ОДПФ.
5.	Существуют методы быстрого преобразования Фурье, позволяющие существенно сократить число операций, выполняемых при расчете ЦФ спектральными методами.
6.	При анализе и синтезе ЦФ широко используется Z-преобразование для получения спектральных характеристик входного и выходного сигналов и самого цифрового фильтра (его системной функции H (z)). Обратным Z- преобразованием определяются временные характеристики входных и выходных сигналов, а также ЦФ.
7.	Частотный коэффициент передачи ЦФ определяется системной функцией фильтра при z = e^j ^ωΔ.
8.	Линейные стационарные цифровые фильтры с финитной импульсной характеристикой реализуются трансверсальной схемой, а с неограниченной импульсной характеристикой – рекурсивной схемой (с обратной связью с выхода на вход).
9.	Рекурсивные цифровые фильтры устойчивы, если все корни полинома знаменателя системной функции H (z) лежат внутри единичного круга с центром в начале координат.
10.	ЦФ часто строятся по аналоговому эквиваленту. Находят применение методы синтеза ЦФ по заданной импульсной характеристике аналогового эквивалента, по заданному дифференциальному уравнению аналогового эквивалента, по заданной частотной характеристике аналогового эквивалента.
11.	Выходной шум ЦФ, обусловленный квантованием, тем меньше, чем быстрее убывают отсчеты импульсной характеристики.
12.	Выходной шум цифрового перемножителя зависит как от значений отсчетов перемножаемых сигналов, так и от их цифровых компонентов.

Дата добавления: 2014-11-06