И нормального шума на частотный детектор

Совместное воздействие гармонического сигнала

Структурная схема частотного детектора:

Сигнал на выходе амплитудного ограничителя представляет собой частотно-модулированное колебание

,

а помеха – случайный нормальный процесс со спектральной плотностью W ₀, равномерной в полосе пропускания ФПЧ (w_д). Полоса пропускания ФНЧ от 0 до W_max, где W_max –– наивысшая частота модуляции. Помеху запишем в виде

.

Рассмотрим два режима:

1. При отсутствии полезной частотной модуляции cуммарное колебание на выходе ограничителя равно

,

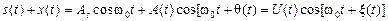где –– амплитуда,

–– фаза.

На выходе резонансного ограничителя колебательный контур настроен на частоту w₀. Обозначив порог ограничителя через U _пор, получим

.

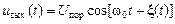Напряжение на выходе частотного детектора пропорционально значению мгновенной частоты входного сигнала (производной от полной фазы сигнала) и в отсутствие полезной модуляции является помехой:

,

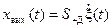где S _ЧД –крутизна характеристики частотного детектора.

На практике обычно выполняется соотношение

,

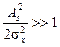поэтому выражение для фазы можно упростить:

.

При изучении теории узкополосных процессов было показано, что функция 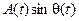для гауссового шума обладает нормальным законом распределения и энергетическим спектром 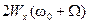, где W _х – спектральная плотность шума на частоте (w₀+W). Таким образом,

.

При дифференцировании нормального случайного процесса распределение остается нормальным. Следовательно, при высоком отношении сигнал/шум на входе частотного детектора процесс на выходе остается также нормальным. Таким образом,

.

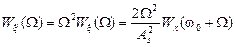Отсюда энергетический спектр помехи на выходе частотного детектора

.

Корреляционная функция помехи на выходе ФНЧ:

.

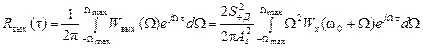Дисперсия (средняя мощность помехи):

.

2. Случай тональной модуляции (режим частотной модуляции, при котором напряжение на выходе частотного детектора пропорционально девиации частоты). При этом . Следовательно, отношение сигнал/шум на выходе

.

Предположим, что шумовой процесс на входе является белым шумом со спектральным шумом 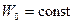, тогда

.

Отсюда

,

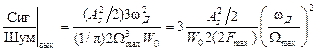где 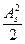–– мощность сигнала на входе, –– мощность шума в двух полосах пропускания. В соответствии с этим

,

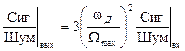где –– индекс угловой модуляции.

ВЫВОД. Увеличивая индекс угловой модуляции, можно получить большой выигрыш в величине сигнал/шум в частотном детекторе по сравнению с величиной сигнал/шум в амплитудном детекторе.

Этот выигрыш будет иметь место, пока справедливо соотношение «сигнал больше помехи» и пока обеспечивается полное ограничение амплитуды колебания на входе детектора, иначе будет наблюдаться эффект гашения сигнала помехой.

Выводы

1.	В нелинейных безынерционных элементах основная трудность состоит в нахождении корреляционной функции. Поэтому общих методов анализа преобразования случайных процессов в нелинейных устройствах не существует.
2.	Спектр на выходе нелинейного безынерционного элемента существенно отличается от спектра на входе и имеет 3 составляющие.
3.	Ширина выходного спектра линейного амплитудного детектора в раз больше ширины входного спектра. Он воспроизводит огибающую узкополосного колебания независимо от особенностей структуры его спектра, т. е. огибающая каждой реализации шума на выходе детектора обладает спектром более широким, чем частотная полоса самой реализации.
4.	Спектры на выходах квадратичного и линейного детекторов одинаковы по форме, отличаются только масштабом оси ординат. Сам сигнал на выходе отличается от сигнала на входе.
5.	Слабый сигнал в линейном детекторе подавляется помехой. При сильном сигнале помеха подавляется сигналом.
6.	При сильном сигнале отношение сигнал/шум на выходе квадратичного детектора в четыре раза меньше, чем у линейного.
7.	Наличие амплитудной модуляции сигнала не вносит существенных изменений в оценку отношения сигнал/шум на выходе детектора. Все результаты не зависят от соотношения между несущей частотой сигнала и мгновенной частотой помехи, т. е. наложение паразитной частотной или фазовой модуляции не оказывает существенного влияния на оценку отношения сигнал/шум на выходе детектора.
8.	Увеличивая индекс угловой модуляции, можно получить большой выигрыш в величине сигнал/шум в частотном детекторе по сравнению с величиной сигнал/шум в амплитудном детекторе.

Дата добавления: 2014-11-06