Работающих по методу обката

Нарезание конических зубчатых колес на станках,

Станки для обработки конических зубчатых колес

Станки для обработки конических зубчатых колес работают по методу копирования или по методу обката.

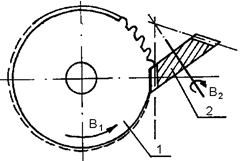
Зубья конических колеc можно нарезать по методу копирования на станках, работающих островершинным резцом по шаблону дисковой или пальцевой модульном фрезой, круговой протяжкой 1 (рис.62,а) и торцовой резцовой головкой (рис.62,б). Из перечисленных инструментов наиболее производительной является обработка круговой протяжкой.

а) б)

Рис.62. Нарезание зубьев:

а – круговой протяжкой; б – торцовой резцовой головкой

При рассмотрении обработки конических зубчатых колес по методу обката изучается взаимодействие нарезаемого колеса с воображаемым производящим колесом в виде плоского (или плосковершинного колеса).

Плоским колесом называется предельное коническое колесо, с углом при вершине начального конуса 2φ = 180°.

Профиль зуба плоского колеса прямобочный. Зацепление плоского колеса с коническим колесом показано на рис.63.

На рис.64 показана принципиальная схема нарезания впадины конического колеса одним резцом при единичном делении.

Если представить плоское колесо 1, у которого из Z _пр зубьев оставлен лишь один 2 в позиции А, этот зуб заточен как строгальный резец и имеет возможность совершать возвратно-поступательное движение П ₁, можно понять суть процесса формообразования впадины конического колеса 3. Плоскому колесу задается медленное вращение В ₂, а заготовка получает связанное с ним движение В ₃, так как если бы в зацеплении была коническая пара .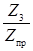

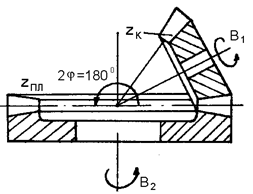
Рис.63. Схема зацепления плоского колеса с коническим колесом

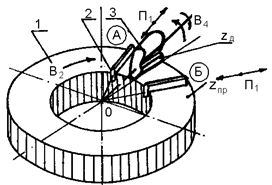
Рис.64. Схема нарезания колеса одним резцом

При движениях из позиции А резец, совершающий строгание П ₁, будет постепенно врезаться во вращающуюся заготовку и, достигнув позиции Б, прорежет одну впадину эвольвентного профиля. Обеспечив движение деления В ₄‑ поворот заготовки на 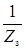оборота и повторив цикл, можно нарезать вторую впадину и т.д.

Можно представить плоское колесо с дуговым зубом, образованным участком а – в резцовой головки 3 (рис.65). Резцовая головка получает независимое вращение В ₁- главное движение, необходимое для формирования впадины по ее длине. При вращении В ₂ воображаемого плоского колеса 1 из позиции А в позицию Б и связанном с ним вращении В заготовки 4 на последней будет сформирована впадина, имеющая эвольвентный профиль и длине форму дуги.

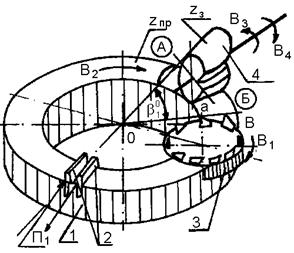
Рис.65. Резцовая головка

Наибольшее число выпускаемых станков для обработки конических колес работает либо резцовой головкой, обеспечивая дуговой зуб, либо двумя резцами 2 (рис.65), формирующими не впадину, как показано на рис.64, а зуб колеса и обеспечивающими прямой или тангенциальный зуб по длине.

Дата добавления: 2014-11-06