
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Средние показатели ряда динамики
|
|
|
|
| Наименование показателя | Метод расчета |
1. Средний уровень ряда 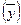 :
а) для интервального ряда при равных интервалах :
а) для интервального ряда при равных интервалах
| 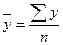
|
| б) для интервального ряда при неравных интервалах | 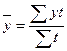
|
| в) для моментного ряда с равностоящими датами | 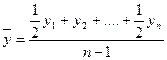
|
| г) для моментного ряда с неравностоящими датами | 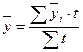
|
2. Средний абсолютный прирост (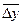 ) )
| 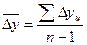 или или 
|
3. Средний коэффициент роста (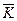 ) )
| 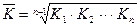 или или 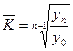
|
4. Средний темп роста (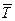 ) )
| 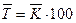 или или 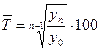
|
5. Средний темп прироста (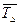 ) )
| 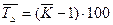 или или 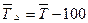
|
Поскольку в нашем примере представленный ряд динамики – моментный ряд с равностоящими датами, то среднегодовая численность населения г. Северодвинска за анализируемый период определим по формуле:
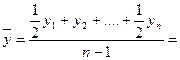
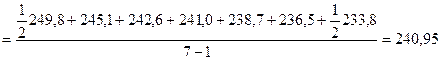 тыс. чел.
тыс. чел.
Средний годовой абсолютный прирост численности населения определим по формуле:
 =
= 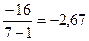 тыс. чел.
тыс. чел.
Следовательно, за анализируемый период с 1992 г. по 1998 г. численность населения г. Северодвинска уменьшалась ежегодно в среднем на 2,67 тыс. чел.
Среднегодовой темп роста численности населения за 1992 – 1998 гг. рассчитаем двумя способами:
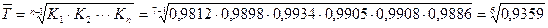 = 0,989
= 0,989
или 98,9 %.
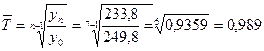 или 98,9 %.
или 98,9 %.
Среднегодовой темп прироста получим, вычтя из среднего темпа роста 100 %.
В нашем примере
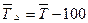 = 98,9 % - 100 % = -1,1 %.
= 98,9 % - 100 % = -1,1 %.
Это означает, с 1992 г. по 1998 г. население г. Северодвинска уменьшалось ежегодно на 1,1 %.
Методы расчета среднего уровня интервального и моментного рядов динамики различны. Рассмотрим это на примерах.
Пример 2. По данным статистической отчетности оборот розничной торговли г. Северодвинска (млн. руб.) за 1999 – 2003 гг. составляет:
| Год | |||||
| Оборот розничной торговли, млн. руб. | 2076,3 | 3003,7 | 4497,6 | 5390,5 | 6185,1 |
Средний уровень оборота розничной торговли за 1999 -2003 гг. находим по формуле средней хронологической для интервального ряда с одинаковыми интервалами:
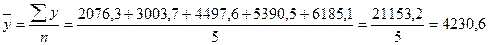 млн. руб.
млн. руб.
Пример 3. Списочная численность работников цеха на 1-е сентября т.г. составляет 125 чел. В сентябре идет следующее движение по кадрам: 3 сентября было принято на работу 2 чел; 9 сентября уволилось 3 чел; 18 сентября было принято 4 чел; 27 сентября уволилось 2 чел. Определить среднедневную списочную численность работников цеха за сентябрь т.г.
Средний уровень интервального ряда с неравностоящими уровнями по формуле средней арифметической взвешенной:
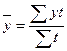 .
.
Для расчета средней численности работников определим продолжительность t каждого календарного периода с постоянной численностью работающих и общее число человеко-дней.
Таблица 5.4
Вспомогательная таблица для расчета среднедневной списочной
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 549; Нарушение авторских прав?; Мы поможем в написании вашей работы!