P.S. Не забудьте прихватить с собой небольшой сувенирчик. Будем обмениваться подарками. 1 страница

10. Отечественные теории этноса.

Cosx

НЕ

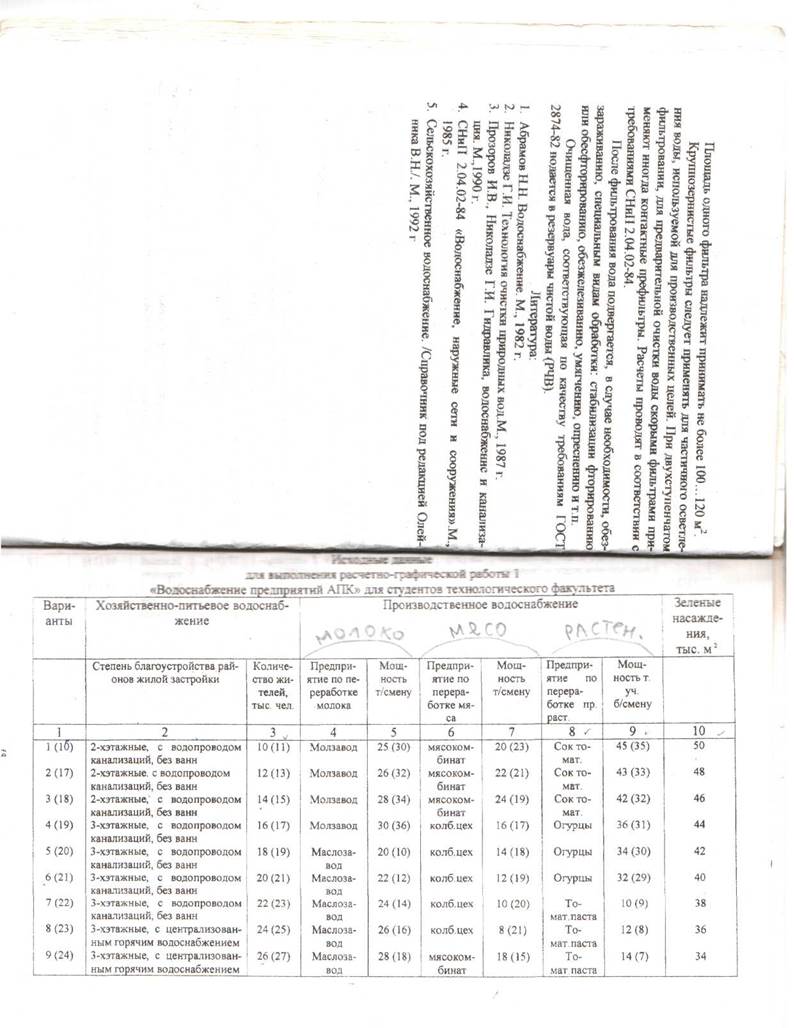
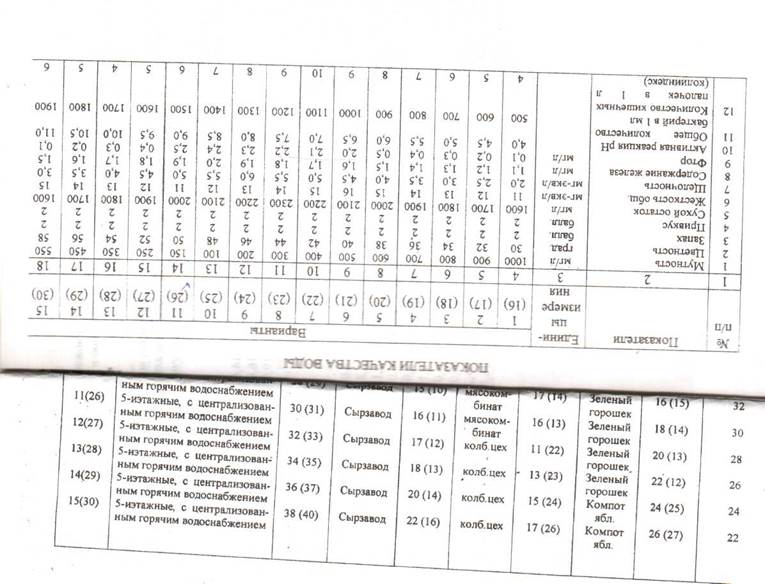
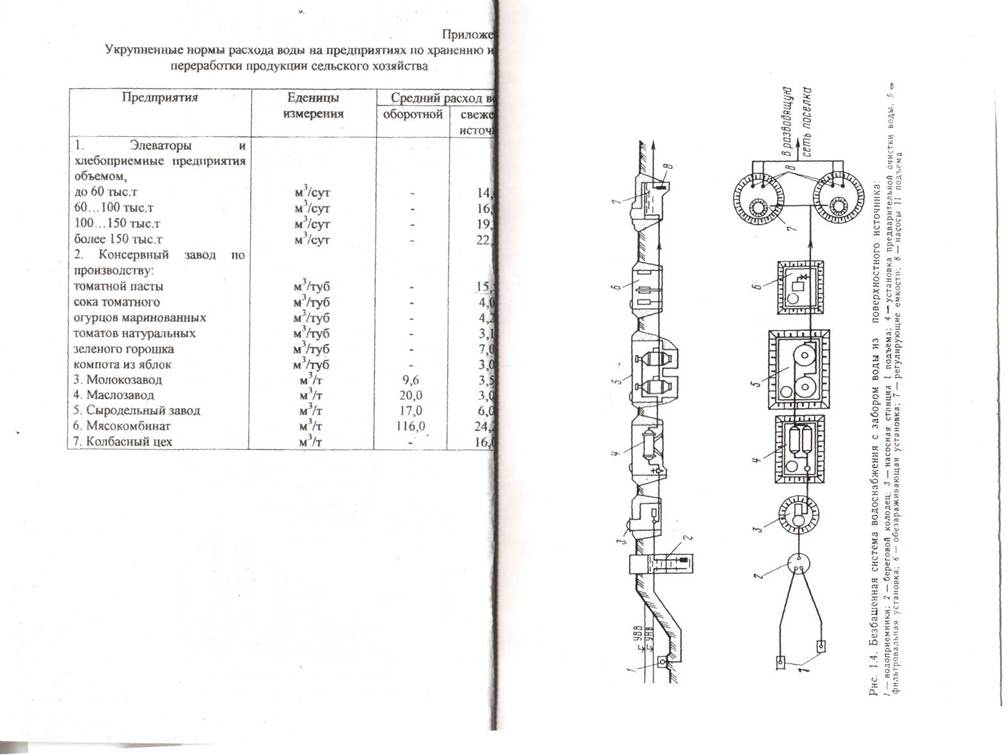
Исходные данные к курсовой работе

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

J

Г

..

..

..

..

..

..

..

^ИЯ

1) Дьяконов В.П. Система Mathcad: Справочник.- М.: Радио и связь, 1993.- 128 с.

2) Макаров И.М., Менский Б.М. Линейные автоматические системы. М.: Машиностроение, 1982,- 504 с.

3) Попов Е.П. Теория линейных систем автоматизированного управления и регулирования – М.: Наука, ГРФМЛ, 1989.- 304 с.

4) Очков В.Ф. Mathcad Plus 6.0 для студентов и инженеров.- М.: Компьютер Пресс, 1996. – 238 с.

5) Лебедев Ю.М. Теория автоматического управления. Система Mathcad и ее применение для расчетов. – Томск, 1996. – 71 с.

Приложение 1

Таблица П1

Продолжение таблицы П1

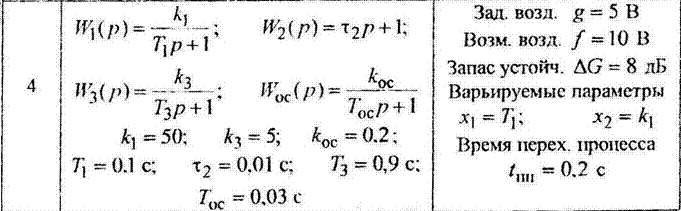
Продолжение таблицы П1

Продолжение таблицы П1

Продолжение таблицы П1

Продолжение таблицы П1

Продолжение таблицы П1

Продолжение таблицы П1

}dx.

Энергия же изгиба есть

к"Е г I &1 \2 F_mn = 2nR sin a _24(j__p.₂₎ J [jtf) dx.

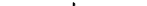Варьируя сумму F_Ba = + ^"апл ^п0 £> получим уравнение

dx*

d%, 12(1—о²)

-1 = 0.

PR*

При х -+ оо £ должно стремиться к нулю, а при х = 0 должны выполняться граничные условия равенства нулю момента сил: £"= О, и условие равенства развивающейся при изгиСэ силы нормальной к поверхности оболочки ком­поненте силы тяжести:

2nR sin а ■

■h³E

12(1 — о²)

■ = Q cos а.

• cos хх,

Удовлетворяющее этим условиям решение есть

1 = Ае~^КХ-

где

_ [ 3(1 — а²) ] 1/4 „ Qctgoc f 3/?² (1 —а²) 1'

* ~ L h*R* J ' ^Л~ й [ 8лА² J Величина прогиба оболочки есть

d = £ (0) cos а = A cosa.

§ 16. Кручение стержней

Перейдем теперь к изучению деформаций тонких стержней. Этот случай отличается от всех ранее рассматривавшихся тем, что вектор смещения п может быть большим даже при слабой дефор­мации, т. е. при малом тензоре u_ih ¹). Так, при слабом сгибании тонкого длинного стержня его концы могут значительно пере­меститься в пространстве, даже если относительные смещения со­седних точек в стержне малы.

Существует два типа деформаций стержней, могущих сопро­вождаться большим смещением отдельных частей стержня. Одним из них является изгиб стержня, а вторым — его кручение. С рас­смотрения этого второго случая мы и начнем.

¹) Исключением является только простое растяжение стержня без изменения его формы, — при слабом растяжении наряду с тензором всегда мал также в вектор н.

Деформация кручения заключается в том, что в стержне, остающемся при этом прямым, каждое поперечное сечение пово­рачивается относительно ниже лежащих на некоторый угол.

Если стержень длинный, то при слабом кручении достаточно уда­ленные друг от друга сечения могут повернуться на большой угол. Образующие боковой поверхности стержня, параллельные его оси, приобретают при кручении винтовую форму.

Рассмотрим тонкий прямой стержень произвольного сечения. Выберем систему координат с осью z вдоль оси стержня и началом координат где-нибудь внутри него. Введем угол кручения т как угол поворота, отнесенный к единице длины стержня. Это значит, что два бесконечно близких поперечных сече.ния, находящихся на расстоянии dz, поворачиваются друг относительно друга на угол d<p = т dz (так что т = dqldz). Сама деформация круче­ния, т. е. относительные смещения соседних частей стержня, предполагаются малыми. Условием этого является малость отно­сительного поворота сечений, удаленных вдоль длины стержня на расстояния порядка его поперечных размеров R, т. е.

<гЯ«1. (16,1)

Рассмотрим небольшую область длины стержня вблизи начала координат и определим смещения и точек стержня в этой области. В качестве несмещенного выберем поперечное сечение стержня в координатной плоскости х, у. Как известно, при повороте ра­диус-вектора г на малый угол бф смещение его конца определяется формулой

Ьг = lfi?r], (16,2)

где бф — вектор с абсолютной величиной, равной углу поворота, направленный вдоль оси, вокруг которой производится поворот. В нашем случае поворот производится вокруг оси г, причем для точек с координатой z угол поворота относительно плоскости х, у равен xz (угол т в области вблизи начала координат можно рас­сматривать как постоянный). Формула (16,2) дает теперь для компонент а_х, и_у вектора смещения

и_х = —xzy, и_у = xzx. (16,3)

При кручении стержня его точки испытывают, вообще говоря, также и смещение вдоль оси г. Поскольку при т = 0 это смещение отсутствует, то при малых т его можно считать пропорциональ­ным т. Таким образом,

u_z = тф (х, у), (16,4)

где[(1р (х, у) — некоторая функция от х и у, называемая функцией кручения. В результате описываемой формулами (16,3) и (16,4) деформации каждое поперечное сечение стержня поворачивается вокруг оси z, одновременно искривляясь, переставая быть пло­ским. Следует заметить, что, выбрав определенным образом на­чало координат в плоскости х, у, мы тем самым «закрепляем» определенную точку сечения стержня так, что она не смещается в этой плоскости {смещаясь, однако, вдоль оси z); изменение вы­бора начала координат не отразилось бы, разумеется, на самой деформации кручения, приведя лишь к несущественному общему смещению стержня как целого.

Зная и, можно найти компоненты тензора деформации. По­скольку и в рассматриваемой области мало, то можно воспользо­ваться формулой u_ih = -i- (-J^+ • В результате находим

"жж ⁼ Uyy = U_Xy = и_гг = о,

"~=-И"!?- =i~(w^+x)' ⁽¹⁶'⁵⁾

Обращаем внимание на то, что иц = 0; другими словами, круче­ние не сопровождается изменением объема, т. е. представляет собой деформацию чистого сдвига.

Для компонент тензора напряжений находим

о_хх = Оуу = o_zz = о_ху — 0,

а_жг = 2ры_жг = рт — а_у1 = 2ри^ = рт + (16,6)

(здесь удобнее пользоваться модулем сдвига р, вместо Е и о). Поскольку отличны от нуля только o_xz и о_уг, то общие уравнения равновесия do_ih/dx_h = 0 сводятся к уравнению

Подставив сюда (16,6), мы найдем, что функция кручения должна удовлетворять уравнению

Аг|) = 0, (16,8)

где А — двухмерный оператор Лапласа.

Несколько более удобно, однако, пользоваться другой вспомо­гательной функцией х (х, у), определяемой равенствами

o_xz = 2рт o_yz = - 2рт ||; (16,9)

для этой функции получаются более удобные граничные условия на контуре сечения стержня (см. ниже). Сравнив (16,9) с (16,6), получим

Sh*+²f- ОМ?)

Дифференцируя первое равенство по у, второе по х и вычитая одно из другого, получим для функции х следующее уравнение:

Ах = -1. (16,П)

Для определения граничных условий на поверхности стержня замечаем, что благодаря малой толщине стержня действующие на его боковую поверхность внешние силы малы по сравнению с возникающими в стержне внутренними напряжениями и потому могут быть положены (при отыскании граничных условий) рав­ными нулю. Это обстоятельство в точности аналогично тому, что мы имели при рассмотрении изгиба тонких пластинок. Таким образом, на боковой поверхности стержня должно быть o_ihn_k = 0; поскольку ось z направлена по оси стержня, то вектор нормали г» имеет только компоненты п_х, п_у, так что написанное уравнение сводится к условию

Подставляя сюда (16,9), получаем

Но компоненты вектора нормали к плоскому контуру (контуру

. dy - dx

сечения стержня) равны п_х — —п_д = —ц-, где х, у— коорди­наты точек контура, a dl — элемент дуги. Таким образом, полу­чаем

откуда % — const, т. е. на контуре се­чения функция х постоянна. Поскольку в определения (16,9) входят только про­изводные от функции х, то ясно, что к этой функции можно прибавлять любую по­стоянную. Если контур сечения одно-связен, то можно, следовательно, без

всякого ограничения общности положить на нем в качестве гра­ничного условия к уравнению (16,11) ^х)

X = 0. (16,12)

*) Задача об определении деформации кручения по уравнению (16,11) с гра­ничным условием (16,12) формально совпадает с задачей об определении формы прогиба равномерно нагруженной плоской мембраны по уравнению (14,9). Полезно заметить также гидродинамическую аналогию: уравнением вида (16,11) определяется распределение скоростей, а {х, у) вязкой жидкости по сече­нию трубы; граничному условию (16,12) соответствует условие v — 0 на непо­движных стенках трубы (см. VI, § 17).

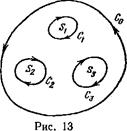
В случае же многосвязного контура % будет иметь различные постоянные значения на каждой из замкнутых кривых, состав­ляющих контур. Поэтому положить х равным нулю можно будет лишь на одной из этих кривых, например на внешнем контуре (С₀ на рис. 13). Значения же х на остальных частях контура опре­делятся из условия, являющегося следствием однозначности сме­щения и_г — тф (х, у) как функции координат. Именно, ввиду однозначности функции кручения \р (х, у) интеграл от ее диффе­ренциала dip по замкнутому контуру должен быть равен нулю. С помощью соотношений (16,10) имеем поэтому

$*.-$(£^л+$*)- -

или

§2Ldl = -S, (16,13)

где д%/дп есть производная функции % по направлению внешней нормали к контуру, a S — охватываемая этим контуром площадь. Применяя (16,13) к каждой из замкнутых кривых С_х, С₂, мы и получим искомые условия.

Определим свободную энергию подвергнутого кручению стержня. Для энергии единицы объема имеем

F = °JfL _{= 0хг}и_хг + а_уги_уг = ± (ah + а%) и, подставляя сюда (16,9):

^ [(*)'+(^.)'] в ^(ИЛ

где V означает двухмерный градиент. Энергия кручения, отне­сенная к единице длины стержня, получится отсюда интегрирова­нием по площади поперечного сечения, т.е. равна Ст²/2, где коэф­фициент С равен

C = 4₁xJ(vxM-

Величину С называют крутильной жесткостью стержня. Полная упругая энергия стержня равна интегралу

F_c^\-\Cx*dz, (16,14)

взятому по его длине. Написав

(VX)^a = V (X VX) - X Н = V (X VX) + X и преобразуя интеграл от первого члена в интеграл по линии контура сечения стержня, получим

C = 4ji(j>x|£<M + 4!i Jxd/- (16,15)

Если контур сечения односвязен, то ввиду граничного условия X = 0 первый член исчезает и остается

C = ty\₁dxdy. (16,16)

Для многосвязной же границы (рис. 13), положив % = 0 на внеш­нем контуре С₀ и обозначив посредством Xs постоянные значе­ния х ^на внутренних контурах C_h, получим с помощью (16,13)

C = 4ii2fcS» + 4|iJxd*rfj, (16,17)

к

(следует помнить, что при интегрировании в первом члене в (16,15) контур С₀ обходится в прямом, а контур С_к — в обратном направ­лениях).

Рассмотрим наиболее обычный случай кручения, когда один из концов стержня закреплен неподвижно, а внешние силы при­ложены только к поверхности другого его конца. Эти силы та­ковы, что производят только кручение стержня без какой бы то ни было другой его деформации, например изгиба. Другими словами, они составляют некоторую пару сил, закручивающую стержень вокруг его оси. Момент этой пары обозначим посред­ством М.

Естественно ожидать, что в таком случае угол кручения х постоянен вдоль длины стержня. В этом можно убедиться, напри­мер, из условия минимума полной свободной энергии стержня в равновесии. Полная энергия деформированного стержня равна сумме F_CT + U, где U — потенциальная энергия, обусловлен­ная действием внешних сил. Подставляя в (16,14) х — dqldz и варьируя по углу ф, находим

или, интегрируя по частям,

- j C-jg- бф dz -f W + Стбф = 0.

В последнем члене слева берется разность значений на пределах интегрирования, т. е. на концах стержня. Один из этих концов, скажем нижний, закреплен так, что на нем бф = 0. Что касается вариации бV потенциальной энергии, то, взятая с обратным зна­ком, она представляет собой работу внешних сил при повороте на угол бф. Как известно из механики, работа пары сил при таком повороте равна произведению УИбф угла поворота на момент пары. Поскольку никаких других внешних сил нет, то 61/ = —Мбф, и мы получаем

jC-~b<pdz + 8q>{— М+С%) = 0. (16,18)

Во втором члене берется его значение на верхнем пределе. В инте­грале по dz вариация бф произвольна, а потому должно быть С dxldz = 0, т. е.

х ~ const.

(16,19)

Таким образом, угол кручения постоянен вдоль всей длины стержня. Полный угол поворота верхнего основания относительно нижнего равен поэтому просто произведению т/ угла т на длину / стержня.

В уравнении (16,18) должен исчезнуть также и второй член. Отсюда находим следующее выражение для постоянного угла кручения:

т = М/С. (16,20)

Задачи

1. Определить крутильную жесткость стержня с круговым сечением (ра-
диуса R).

Решение. Решения задач 1—4 формально совпадают с решениями задач о движении вязкой жидкости в трубе соответствующего сечения (см. при­мечание на с. 89); количеству Q протекающей через сечение трубы жидкости соответствует здесь величина С.

Для стержня кругового сечения имеем (начало координат в центре сечения) 5С=1/₄(/??-^-^),

Крутильная жесткость:

С = цлЯ*/2.

Для функции 1|> получаем из (16,10) i|>= const. Но постоянная тр соответствует, согласно (16,4), простому смещению стержня как целого вдоль оси г; поэтому можно считать, чтогр = 0. Таким образом, поперечные сечения кругового стержня при кручении остаются плоскими.

2. То же для стержня эллиптического сечения (полуоси а и Ь).
Решение, Крутильная жесткость:

^C==JtL1 а* + Ь* •

Распределение продольных смещений дается функцией кручения:

б² - а²

(оси координат направлены по осям эллипса).

3. То же для стержня с сечением в виде равностороннего треугольника
(длина сторон а).

Решение. Крутильная жесткость:

Функция кручения;

t = -~y(xV3 +y){xV3-у),

причем начало координат выбрано в центре треугольника, а ось х совпадает с од­ной из его высот.

4. То же для стержня, имеющего вид длинной тонкой пластинки (ширина d, толщина h < d).

Решение. Задача эквивалентна задаче о течении вязкой жидкости между плоскопараллельными стенками. Результат:

С = и dh³/3.

5. То же для цилиндрической трубы (внутренний и внешний радиусы Rf
Решение. Функция

x = V.

(в полярных координатах) удовлетворяет условию (16,13) на обеих границах кольцевого сечения трубы. По формуле (16,17) найдем

с =-1-й (Я!-Я!).

6. То же для тонкостенной трубы произвольного сечения.
Решение. Ввиду тонкости стенки трубы можно считать, что на протя-
жении ее ширины Л функция % меняется от нуля на одной стороне до Xi ^на Дру-
гой по линейному закону % — Xiljlh (У — координата вдоль толщины стенки).
Тогда условие (16,13) дает %-yLlh = S, где L — длина периметра сечения трубы,
a S — охватываемая им площадь. В выражении (16,17) второй член мал по сравне-
нию с первым, и мы получаем

С = 4hS*yJL.

Если трубу разрезать продольно по одной из ее образующих, то крутильная жесткость резко уменьшается, становясь равной (согласно результату задачи 4) С = ц/Л³/3.

§ 17, Изгиб стержней

В изогнутом стержне в некоторых местах его происходит растяжение, а в других — сжатие. Растянуты линии на выпуклой стороне изогнутого стержня, а на вогнутой стороне происходит сжатие. Как и в случае пластинок, вдоль длины стержня внутри него существует «нейтральная» поверхность, на которой не про­исходит ни растяжения, ни сжатия. Она отделяет собой области сжатия от областей растяжения.

Начнем с исследования деформации изгиба в небольшом уча­стке длины стержня, в котором изгиб можно считать слабым; под слабым мы понимаем здесь изгиб, при котором мал не только тензор деформации, но и абсолютная величина смещений точек стержня. Выберем систему координат с началом в некоторой точке нейтральной поверхности внутри рассматриваемого участка стержня. Ось z направим параллельно оси стержня (недеформи-рованного); изгиб пусть происходит в плоскости г, х. При слабом изгибании стержня можно считать, что изгиб происходит в одной плоскости. Это связано с известным из дифференциальной гео­метрии обстоятельством, что отклонение слабо изогнутой кривой от плоскости (так называемое ее кручение) является малой ве­личиной высшего порядка по сравнению с кривизной.

Аналогично тому, что мы имели в случае изгиба пластинок и кручения стержней, и при изгибе тонких стержней внешние силы, действующие на боковую поверхность стержня, малы по сравнению с возникающими внутри стержня напряжениями, и при определении граничных условий на этой поверхности их можно считать равными нулю. Таким образом, вдоль всей боковой поверхности стержня имеем o_ikn_h = 0, или, поскольку n_t = О,

+ о_хуп_у = О

и аналогично для i = у, г. Выберем такую точку на контуре по­перечного сечения стержня, в которой нормаль п направлена параллельно оси х. Другая такая же точка имеется где-нибудь на противоположной стороне контура. В обеих этих точках п_у = = 0, и из написанного выше равенства имеем о_хх — 0. Но по­скольку самый стержень предполагается тонким, то, если а_хх исчезает на двух сторонах его сечения, оно мало и вдоль всего сечения, так что можно положить а_хх = 0 во всем стержне. Аналогичным образом убеждаемся в том, что все компоненты тензора напряжений должны быть равными нулю, за исключением только компоненты o_zz. Другими словами, при изгибе тонкого стержня большой является только растягивающая (или сжима­ющая) компонента тензора внутренних напряжений. Деформа­ция, в которой отлична от нуля только компонента а_гг тензора напряжений, есть не что иное, как деформация простого растя­жения или сжатия (§ 5). Таким образом, в каждом элементе объема изгибаемого стержня происходит простое растяжение (или сжатие). Самая величина этого растяжения, конечно, раз­лична в разных точках каждого из поперечных сечений стержня, что и приводит в результате к изгибу всего стержня.

Легко определить величину относительного растяжения в каж­дой точке стержня. Рассмотрим какой-нибудь элемент длины dz, параллельный оси стержня и находящийся где-нибудь вблизи начала координат. При изгибании стержня длина dz изменится, сделавшись равной dz'. Неизменными остаются только те элементы длины, которые расположены на нейтральной поверхности. Пусть R есть радиус кривизны нейтральной поверхности вблизи начала координат. Длины dz и dz' можно рассматривать как элементы дуги окружностей с радиусами соответственно R и R + х, где * — значение координаты х в точке, в которой выбран элемент dz'. Поэтому

dz' = -«±±-dz=(l+±)dz.

Относительное удлинение равно, следовательно,

dz' — dz х

Tz " R '

С другой стороны, относительное удлинение элемента длины dz равно компоненте u_it тензора деформации. Следовательно,

(17,1)

Мы можем написать теперь a_zz, воспользовавшись непосредст­венно соотношением a_zz = Eu_zz, имеющим место при простом растяжении. Таким образом,

о_а=--^Е. (17,2)

До сих пор еще расположение нейтральной поверхности в изо­гнутом стержне оставалось неопределенным. Его можно опре­делить из условия, что рассматриваемая нами здесь деформация должна представлять собой чистый изгиб, без какого бы то ни было общего растяжения или сжатия стержня. Для этого полная сила внутренних напряжений, действующая на поперечное сече­ние стержня, должна быть равной нулю, т. е. должен исчезать интеграл

\ozzdf,

взятый по этой поверхности. В связи с выражением (17,2) для о_гг это приводит к условию

\xdf = Q. (17,3)

С другой стороны, можно ввести понятие о центре инерции сечения стержня, как о центре инерции однородного плоского диска соответствующей формы. Координаты этого центра:

\xdfj\df, \ydfj\df.

Таким образом, условие (17,3) означает, что в системе координат с началом, лежащим на нейтральной поверхности, дг-координата центра инерции сечения стержня равна нулю. Другими словами, нейтральная поверхность проходит через центры инерции попе­речных сечений стержня.

Помимо и_гг, отличны от нуля еще две компоненты тензора деформации, так как при простом растяжении имеем и_хх = u_vy — = —au_zz. Зная тензор деформации, легко найти также и смеще­ния точек. Пишем:

дЧг _ х ди_х _______ ди_уах

"» dT~~R' ~ШГ~~~1у~—~ R '

fax. ди_г _ _п ди_х ди_у _ _п диу _j_ ди_{2 п} дг ~т~ дх ~ ' ду ^ дх ~ ^и' ~дТ~ ^ ду '

Интегрирование этих соотношений приводит к следующим выра­жениям для компонент перемещения:

Постоянные интегрирования положены равными нулю; это зна­чит, что мы закрепляем в пространстве положение начала коорди­нат.

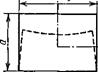
Из формул (17,4) видно, что точки, расположенные в попереч­ном сечении г — const = г₀, после изгиба заполняют поверхность

z = z₀ + и_г = z₀ (1 + -j-).

Мы видим, что в рассматриваемом приближении сечения остаются
при изгибе плоскими, лишь поворачиваясь на некоторый угол
_ относительно своего первоначального по-

ложения. Форма же сечения меняется; так при изгибе стержня прямоугольного сече­ния (со сторонами а и Ь) боковые стороны ^ контура сечения у — ±Ы2 после изгиба У занимают положения

*=_±-f-+^=±4(i-^-),

Рис. 14

т. е. становятся наклонными, оставаясь прямыми. Верхняя же и нижняя стороны х = ±а!2 изгибаются в параболические кривые (рис. 14):

*=±'-f+ «,= ±-Y~^-[zl + a (-ip-V)].

Дата добавления: 2014-11-07