Ol — V2X 44 страница

v = Оо cos _Ф (/, (kr) /, (ft) - /, (kr) /,.(*)], х = cos ф [Л (ftr) Л (ft) + /, (ftr) /, (ft)]

(причем градиент dw/dz = 0). Описываемое этими формулами движение анти­симметрично относительно вертикальной плоскости, проходящей через ось трубы и делящей полость на две части; в одной из них жидкости опускается, а в другой поднимается. Написанное решение удовлетворяет условию v — 0 при г = 1. В случае а условие т = 0 приводит к уравнению Л (ft) = 0; его наименьший корень дает критическое число!Й_КР = ft⁴ = 216. В случае б усло­вие dxjdr = 0 приводит к уравнению

h (ft), /о (ft) _ 2 Л (ft) Л {*) ft '

Наименьший корень этого уравнения дает 32„р = 68.

2. Сформулировать вариационный принцип для задачи о собственных зна­чениях 91, определяемых уравнениями (57,12).

Решение. Придадим уравнениям (57,12) более симметричный вид, вве­дя вместо х новую функцию т = У5? т, т. е. снова изменив единицу измере­ния температуры. Тогда:

<\[Ш х n = Vw — Д v, УЯч_г = —Дт, divv = 0. Поступая, как при выводе (57,7), получим У*Я = J/N, где

J = -1 ^ [(rot v)² + (Vt)²] dV, N=^ v_zx dV

(интеграл N положителен, в чем легко убедиться, приведя его к виду

0g-i/2 ^ (Vx)²dV). Вариационный принцип формулируется, как требование

экстремальности / при дополнительных условиях divv = 0 и N = 1. Мини­мальное значение / определяет наименьшее собственное значение У Я.

') Уравнения имеют также решения, периодические вдоль оси г, содер­жащие множитель exp(ikz). Все они, однако, приводят к более высоким зна­чениям 5?_Кр. Обратим внимание на то, что рассматриваемое решение с ft = 0 удовлетворяет также и точным (нелинеаризованным) уравнениям (57,10) ввиду тождественного обращения в нуль нелинейных членов (v?)v и vVt.

ДИФФУЗИЯ

§ 58. Уравнения гидродинамики для жидкой смеси

Во всем предыдущем изложении предполагалось, что жид­кость полностью однородна по своему составу. Если же мы имеем дело со смесью жидкостей или газов, состав которой ме­няется вдоль ее объема, то уравнения гидродинамики суще­ственно изменяются. ' Мы ограничимся рассмотрением смесей с двумя только ком­понентами. Состав смеси мы будем описывать концентрацией с, определяемой как отношение массы одного из входящих в со­став смеси веществ к полной массе жидкости в данном элементе объема.

С течением времени распределение концентрации в жидкости, вообще говоря, меняется. Изменение концентрации происходит двумя путями. Во-первых, при макроскопическом движении жид­кости каждый данный ее участок передвигается как целое с не­изменным составом. Этим путем осуществляется чисто механи­ческое перемешивание жидкости; хотя состав каждого передви­гающегося участка жидкости не меняется, но в каждой данной неподвижной точке пространства концентрация находящейся в этом месте жидкости будет со временем меняться. Если от­влечься от могущих одновременно иметь место процессов теп­лопроводности и внутреннего трения, то такое изменение концен­трации является термодинамически обратимым процессом и не ведет к диссипации энергии.

Во-вторых, изменение состава может происходить путем мо­лекулярного переноса веществ смеси из одного участка жид­кости в другой. Выравнивание концентрации путем такого не­посредственного изменения состава каждого из участков жид­кости называют диффузией. Диффузия является процессом не­обратимым и представляет собой наряду с теплопроводностью и вязкостью один из источников диссипации энергии в жидкой смеси.

Будем обозначать посредством р полную плотность жидкости. Уравнение непрерывности для полной массы жидкости сохра­няет прежний вид

|L + divv = 0. (58,1)

Оно означает, что полная масса жидкости в некотором объеме может измениться только путем втекания или вытекания жид­кости из этого объема. Следует подчеркнуть, что, строго говоря, для жидкой смеси самое понятие скорости должно быть опреде­лено заново. Написав уравнение непрерывности в виде (58,1), мы тем самым определили скорость в соответствии с прежним определением как полный импульс единицы массы жидкости.

Не меняется также и уравнение Навье-Стокса (15,5). Выве­дем теперь остальные гидродинамические уравнения для смесей.

При отсутствии диффузии состав каждого данного элемента жидкости оставался бы неизменным при его передвижении. Это

значит, что полная производная —■ была бы равна нулю, т. е.

имело бы место уравнение

dc дс. _ _л

Это уравнение можно написать, используя (58,1), как

^- + div(vpc)==0,

т. е. в виде уравнения непрерывности для одного из веществ в смеси (рс есть масса одного из веществ смеси в единице объема). Написанное в интегральном виде

_д_ dt

^ рс dV = — ф pcv d\

оно означает, что изменение количества данного вещества в не­котором объеме равно количеству этого вещества, переносимому движущейся жидкостью через поверхность объема.

При наличии диффузии наряду с потоком vpc данного веще­ства вместе со всей жидкостью имеется еще и другой поток, ко­торый приводит к переносу веществ в смеси даже при отсутствии движения жидкости в целом. Пусть i есть плотность этого диф­фузионного потока, т. е. количество рассматриваемого вещества, переносимого путем диффузии в единицу времени через единицу поверхности¹). Тогда для изменения количества этого вещества в некотором объеме имеем:

-Jj ^ рс dV = — ф pcv df — § i df,

dt

или в дифференциальном виде д (рс)

— div (pcv) — div i. (58,2)

') Сумма плотностей потоков обоих веществ должна быть равна pv. Поэтому если плотность потока одного из них есть pvc -j- i, то другого: pv(l - с) - I.

УРАВНЕНИЯ ГИДРОДИНАМИКИ ДЛЯ ЖИДКОЙ СМЕСИ

С помощью (58,1) это уравнение непрерывности для одного из веществ в смеси можно написать в виде

p(-oT + ^vVc)^==-divi- ^(58>3)

Для вывода еще одного уравнения повторим произведен­ный в § 49 вывод, учитывая, что термодинамические величины жидкости являются теперь функциями также и от концен­трации. При вычислении (в § 49) производной

с помощью уравнений движения нам приходилось, в частности, преобразовывать члены р — и — vVp- Это преобразование те­перь изменяется в связи с тем, что термодинамические соотно­шения для энергии и тепловой функции содержат дополнитель­ный член с дифференциалом концентрации:

de = Т ds + -jjr dp + ц dc, dw — Т ds + у dp + ц dc,

где р, — соответствующим образом определенный химический по­тенциал смеси '). Соответственно этому в производнуюр■—■ вой-

дс _тт

дет теперь дополнительный член pp.Написав второе из тер­модинамических соотношений в виде

dp = pdw — pTds — pp.dc,

мы видим, что в член — v Vp войдет дополнительный член ppv Vc. Таким образом, к выражению (49,3) надо прибавить

РИ (|f + vVc).

') Из термодинамики известно (см. V, § 85), что для смеси двух веществ: de — Т ds — р dV + p,id/u + \i2dn2,

где п„ п_г — числа частиц обоих веществ в 1 г смеси, а Ць [i₂— химические потенциалы этих веществ. Числа /г₄ и п_: удовлетворяют соотношению nimi + пгШг = 1, где mi, шг — массы частиц обоего рода. Если ввести в ка­честве переменной концентрацию с = ti\m_u то мы получим:

de = Т ds — р dV + (— dc.

Сравнивая с приведенным в тексте соотношением, мы видим, что химический потенциал ц, которым мы пользуемся, связан с обычными потенциалами pi и р2 посредством

ц = p-i/mi — ц₂/т₂.

Поэтому к выражению (49,3) надо добавить

рр (дс/dt + vVc) = — ц. div i. В результате получим:

= - div[vp (-у + w) - (voO + q] + _РГ (-g- + Ws) -

-^l^ + divq-pdivi- (58,4)

Вместо — kVT мы пишем теперь некоторый поток тепла q, кото­рый может зависеть не только от градиента температуры, но и от градиента концентрации (см. следующий параграф). Сумму двух последних членов с правой стороны равенства напишем в виде

div q — р div i = div (q — pi) + ' Vp.

Выражение

pv {— -f ш) — (va') + q,

стоящее под знаком div в (58,4), есть, по определению q, пол­ный поток энергии в жидкости. Первый член есть обратимый поток энергии, связанный просто с перемещением жидкости как целого, а сумма —(vcr'J-f-q есть необратимый поток. При отсут­ствии макроскопического движения вязкий поток (vo') исчезает и тепловой поток есть просто q.

Уравнение закона сохранения энергии гласит:

-§t ("IT + ^ре) ⁼ ~ ^div [^pv ("Г + ^w) ~ <^va') + ч] • (58,5)

Вычитая его почленно из (58,4), получим искомое уравнение

_РГ (■§ + v Vs) = a'_ik g- - div (q - pi) - i V|*. (58,6)

обобщающее выведенное ранее уравнение (49,4).

Мы получили, таким образом, полную систему гидродинами­ческих уравнений для жидких смесей. Число уравнений в этой системе на единицу больше, чем в случае чистой жидкости, со­ответственно тому, что имеется еще одна неизвестная функция —■ концентрация. Этими уравнениями являются: уравнения непре­рывности (58,1), уравнения Навье — Стокса, уравнение непрерыв­ности для одной из компонент смеси (58,2) и уравнение (58,6), определяющее изменение энтропии. Надо, впрочем, отметить, что уравнения (58,2) и (58,6) определяют пока по существу только вид соответствующих гидродинамических уравнений, поскольку в них входят неопределенные величины: потоки i и q. Эти урав­нения делаются определенными лишь при подстановке i и q, вы­раженных через градиенты температуры и концентрации; соот­ветствующие выражения будут получены в § 59.

Для изменения полной энтропии жидкости вычисление, пол­ностью аналогичное произведенному в § 49 (с использованием (58,6) вместо (49,4)), приводит к результату

£[_98dV = -\<*=^dV-№dV+.... (58,7)

(члены, обусловленные вязкостью, для краткости не выписы­ваем).

§ 59. Коэффициенты диффузии и термодиффузии

Диффузионный поток вещества i и тепловой поток q возни­кают в результате наличия в жидкости градиентов концентрации и температуры. Не следует при этом думать, что i зависит толь­ко от градиента концентрации, a q — только от градиента тем­пературы. Напротив, каждый из этих потоков зависит, вообще говоря, от обоих указанных градиентов.

Если градиенты температуры и концентрации невелики, то можно считать, что i и q являются линейными функциями от Vp. и vr (от градиента давления — при заданных Vp и V7" — по­токи q и i не зависят по той же причине, которая была уже ука­зана для q в § 49). Соответственно этому напишем i и q в виде линейных функций от градиентов и. и Т:

i = - aV|x - Bvr,

q=_6Vp.-YVr-f pi.

Между коэффициентами В и 6 существует простое соотноше­ние, являющееся следствием принципа симметрии кинетических коэффициентов. Содержание этого общего принципа заключает­ся в следующем (см. V § 120). Рассмотрим какую-нибудь замк­нутую систему и пусть х_и х₂... — некоторые величины, харак­теризующие состояние системы. Их равновесные значения опре­деляются тем, что в статистическом равновесии энтропия 5 всей системы должна иметь максимум, т. е. должно быть Х_а = 0, где Х_а обозначают производные:

Предположим, что система находится в состоянии, близком к равновесному. Это значит, что все х_а лишь мало отличаются от своих равновесных значений, а величины Х_а малы. В системе будут происходить процессы, стремящиеся привести ее в состоя­ние равновесия. Величины х_а являются при этом функциями вре­мени, а скорость их изменения определяется производными по времени х_а; представим последние в виде функций от Х_а и раз­ложим эти функции в ряд. С точностью до членов первого по­рядка имеем:

х_а = — Z ЧаьХъ- (59,2)

Принцип симметрии кинетических коэффициентов Онсагера ут­верждает, что величины у_аь (называемые кинетическими коэф­фициентами) симметричны по индексам а, Ь:

УаЬ = УЬа. (59,3)

Скорость изменения энтропии 5 равна

S = ^ Ха^ха-

а

Пусть теперь сами величины х_а различны в разных точках тела, т. е. каждый элемент объема тела должен характеризоваться своими значениями величин х_а. Другими словами, будем рас­сматривать х_а как функции от координат. Тогда в выражении для 5, кроме суммирования по а, надо произвести также и ин­тегрирование по всему объему системы, т. е.

а

Что касается зависимости между Х_а и х_а, то обычно можно утверждать, что значения х_а в каждой данной точке системы за­висят только от значений величин Х_а в этой же точке. Если это условие выполняется, то можно писать связь между х_а и Х_а для каждой точки в системе, и мы возвращаемся к прежним соотношениям.

В данном случае выберем в качестве величин х_а компоненты векторов i и q — pi. Тогда из сравнения (58,7) с (59,4) видно, что роль величин Х_а будут играть соответственно компоненты векторов T-'Vp и T~²VT Кинетическими же коэффициентами у_аь будут являться коэффициенты при этих векторах в равенствах

, = -аГ(^)-_РЯ(^-). _ч-_ц| = _6Г(^)-уГ²(^).

В силу симметрии кинетических коэффициентов должно быть BP = 67\ т. е.

6 = рТ.

Это и есть искомое соотношение. Мы можем поэтому напи­сать потоки i и q в виде

i = - aVp - р* V7\ q = — pTVp, — уЧТ + pi (59,5)

всего с тремя независимыми коэффициентами: а, 8, у. В выра­жении для теплового потока удобно исключить градиент J7p, выразив его через i и $Т. Сделав это, получим:

i = - aVfi - Svr, (59,6)

q = (n + -^)i-*V7\

где введено обозначение

_{X = Y}_ZL. ₍59₎₇₎

Если поток вещества i отсутствует, то говорят о чистой теп­лопроводности. Для того чтобы было i =0, Т и и. должны удов­летворять уравнению aVp.+ BVT = 0, или

ady, + $dT = 0.

Интегрирование этого уравнения приводит к соотношению вида f(c,T) = 0, не содержащему в явном виде координат (химиче­ский потенциал является функцией не только от с, Т, но и от давления; в равновесии, однако, давление постоянно вдоль тела, и потому мы полагаем р = const). Это соотношение определяет связь между концентрацией и температурой, которая должна иметь место для отсутствия потока вещества. Далее, при i = 0 имеем из (59,7) q = —xVT"; таким образом, х является не чем иным, как теплопроводностью.

Перейдем теперь к обычным переменным р, Т и с. Имеем:

Последний член можно преобразовать, используя термодинами­ческое соотношение

dro = — sdT + Vdp + tide, (59,8)

где ф — термодинамический потенциал единицы массы, V — удельный объем. Имеем:

(д\х\ _ д\ _(дУ\ \др)с,Т дрдс V дс)р,г'

Подставив Vp. в (59,6) и введя обозначения

^D=f(£),,•Ф-(*)„+*• w

получим следующие выражения:

I = -pD(vc + -^vr + ^Vp), (59,11)

Коэффициент D называют коэффициентом диффузии; он оп­ределяет диффузионный поток при наличии одного только гра-

диента концентрации. Диффузионный же поток, вызываемый градиентом температуры, определяется коэффициентом термо-диффузии krD (безразмерную же величину кт называют термо­диффузионным отношением). В учете последнего члена в (59,11) может возникнуть необходимость лишь при наличии в жидкости существенного градиента давления, вызванного, например, внеш­ним полем. Величину k_pD можно назвать коэффициентом баро-диффузии; мы вернемся еще к этой величине в конце параграфа.

В чистой жидкости диффузионный поток, разумеется, отсут­ствует. Поэтому ясно, что коэффициенты kr и k_p должны обра­щаться в нуль на обоих пределах: с == 0 и с = 1.

Условие возрастания энтропии накладывает определенные ограничения на коэффициенты в формулах (59,6). Подставив эти формулы в выражение (58,7) для скорости изменения энтропии, получим:

±^_PsdV = \^P^dV + \-£_FdV+... (59,13)

Отсюда видно, что наряду с известным уже нам условием % > О должно выполняться также условие а > 0. Имея в виду, что со­гласно одному из термодинамических неравенств всегда

(*).,>»'

(см. V, § 96), мы находим, что должен быть положителен коэф­фициент диффузии: D > 0. Величины же ft г и k_p могут быть как положительными, так и отрицательными.

Мы не станем выписывать громоздких общих уравнений, по­лучающихся при подстановке полученных здесь выражений для i и q в уравнения (58,3), (58,6). Ограничимся лишь случаем, когда нет- никакого существенного градиента давления, а кон­центрация и температура настолько мало меняются в жидкости, что коэффициенты в выражениях (59,11) и (59,12), являющиеся в общем случае функциями от с и 7", можно считать постоян­ными. Будем, кроме того, считать, что в жидкости нет никакого макроскопического движения, помимо того, которое может быть вызвано самим наличием градиентов температуры и концентра­ции. Скорость такого движения будет пропорциональна этим градиентам, и потому в уравнениях (58,3) и (58,6) члены, со­держащие скорость, оказываются величинами второго порядка малости и могут быть опущены. Величиной второго порядка яв­ляется также и член iVp в (58,6). Таким образом, остается

Р-Ц- +divi = 0, рГ-g-+ div (q — pi) = 0.

Подставим сюда для i и q выражения (59,11) и (59,12) (без

ds

члена с Vp), а производную -^т преобразуем следующим

образом:

ds (ds \ dT f^ds\ ^{дс с}р ^дт С^Л ^дс "дТ^КдТ)с,р~ЪТ"^"\дс)т, pW^TlTt \дт)_р, _С~Ы

Здесь учтено, что согласно (59,8):

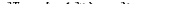(59,15)

Эта система линейных уравнений определяет распределение тем­пературы и концентрации в жидкости.

В особенности важен случай, когда концентрация смеси мала. При стремлении концентрации к нулю коэффициент диффузии стремится к некоторой конечной постоянной, а коэффициент тер­модиффузии— к нулю. Поэтому при малых концентрациях кт мало, и в уравнении (59,14) можно пренебречь членом krST, Оно переходит тогда в уравнение диффузии:

(59,16)

Граничные условия для уравнения (59,16) в разных случаях различны. На границе с поверхностью тела, не растворимого в жидкости, должна обращаться в нуль нормальная к поверх­ности компонента диффузионного потока i = —pDVc; другими словами, должно быть дс/дп — Q. Если же речь идет о диффузии от тела, растворяющегося в жидкости, то вблизи его поверх­ности быстро устанавливается равновесие, при котором концен­трация в примыкающей к поверхности тела жидкости равна концентрации насыщенного раствора с₀; диффузия вещества из этого слоя происходит медленнее, чем процесс растворения. По­этому граничное условие на такой поверхности гласит: с — Cq. Наконец, если твердая поверхность «поглощает» попадающее на нее диффундирующее вещество, то граничным условием являет­ся равенство с = 0 (с таким случаем приходится, например, иметь дело при изучении химических реакций, происходящих на поверхности твердого тела).

Поскольку уравнения чистой диффузии (59, 16) и теплопро­водности имеют одинаковый вид, то все выведенные в §§ 51, 52 формулы могут быть непосредственно перенесены на случай диффузии простой заменой Т на с и % на D. Граничному усло­вию теплоизолированной поверхности соответствует при дйффу­зии условие на нерастворимой твердой поверхности; поверхности же, поддерживаемой при постоянной температуре, соответствует диффузия от поверхности растворяющегося в жидкости тела.

В частности, по аналогии с формулой (51,5) можно написать следующее решение уравнения диффузии:

c{\,t)= ^-^e-W. (59,17)

Оно определяет распределение растворенного вещества в произ­вольный момент времени, если в начальный момент / = 0 все вещество было сконцентрировано в бесконечно малом элементе объема жидкости в начале координат (М — полное количество растворенного вещества).

К сказанному в этом параграфе надо сделать важное заме­чание. Выражения (59,5) или (59,11—12) представляют собой первые неисчезающие члены разложения потоков по производ­ным от термодинамических величин. Как известно из кинетиче­ской теории (см. X, §§ 5, 6, 14), такое разложение является, с микроскопической точки зрения, разложением (для газов) по степеням 1/L отношения длины свободного пробега молекул га­за / к характерной пространственной длине задачи L. Учет чле­нов с производными высших порядков означал бы учет величин более высокого порядка по указанному отношению. Следующи­ми после написанных в (59,5) членов, которые можно образовать из производных от скалярных величин р и Т, были бы члены с производными третьего порядка: grad Ар, и gradAT¹; эти члены заведомо малы по сравнению с уже учтенными в отношении (//Z,)².

Но выражения для потоков могут содержать в себе также и члены с производными скорости. С помощью производных пер­вого порядка, dvi/dxk, можно образовать лишь тензорные вели­чины; это — вязкий тензор напряжений, входящий в состав тен­зора плотности потока импульса. Величины же векторного ха­рактера можно составить из производных второго порядка. Так, в векторе плотности диффузионного потока появятся члены

Г = рЛ,Ду + рл.,^гуу. (59,18)

Требование, чтобы эти члены были малы по сравнению с уже фигурирующими в формулах (59,11 — 12), приводит к дополни­тельным условиям применимости последних. Так, для того чтобы имело смысл оставлять в (59,11) член с Vp и в то же время опу­скать члены (59, 18), должно выполняться условие

--7»^7t.

где р2 — pi — характерный перепад давлений на длине L, a U — характерный перепад скорости (в этой оценке положено k_P ~ 1 — см. задачу). Согласно кинетической теории, D и % выражаются через характеристики теплового движения молекул газа. Уже из соображений размерности очевидно, что X/D ~ 1/vt, где vr — средняя тепловая скорость молекул. Учтя также, что дав­ление газа р ~ pv²-, приходим к условию

Р₂-Р1>Р^4"- <⁵⁹'¹⁹>

Это условие отнюдь не выполняется автоматически. Напро­тив, в важном случае стационарных течений с малыми числами Рейнольдса в диффузионном потоке члены с Vp и с Ду оказы­ваются одинакового порядка величины (Ю. М. Каган, 1962). Действительно, для такого движения градиент давления связан с производными скорости уравнением (20,1)

jVp = v\v (59,20)

(принимаем, что при движении газа его можно считать несжи­маемым). Кинематическая вязкость оценивается как v ~ vrl и потому из этого уравнения находим:

р₂ — Pi ~ ~ pv_TU ~т

•—вместо неравенства в (59,19). Поскольку Ду прямо выражает­ся через Vp согласно (20,1), то необходимость одновременного учета членов с Vp и Ду означает, что бародиффузионный коэф­фициент k_P заменяется «эффективным» коэффициентом

(ApW = fcp—$5"- (59,21)

Обратим внимание на то, что этот коэффициент оказывается в результате кинетической величиной, а не чисто термодинамиче­ской, каковой является согласно (59,10) коэффициент k_p.

Задача

Определить коэффициент бародиффузии для смеси двух идеальных газов. Решение. Для удельного объема имеем:

Г—у (Я1 + П.)

(обозначения — см. примечание на стр.321), а химические потенциалы имеют вид (см. V §93)

|ii-MP. Г) + Лп —qi—, И2 = ЫР. Г) + Пп —З²—.

Числа Л[, п% выражаются через концентрацию газа / согласно «im_t = с, щгпг = 1 — с. Вычисление по формуле (59,10) дает

k_p = (m₂ - m,) с (1 - _с) [±ZLi + ^-].

§ 60. Диффузия взвешенных в жидкости частиц

Под влиянием молекулярного движения в жидкости взвешен­ные в ней частицы совершают беспорядочное броуновское дви­жение. Пусть в начальный момент времени в некоторой точке (начале координат) находится одна такая частица. Ее дальней­шее движение можно рассматривать как диффузию, причем роль концентрации играет вероятность нахождения частицы в том или ином элементе объема жидкости. Соответственно для определе­ния этой вероятности можно воспользоваться решением (59,17) уравнения диффузии. Возможность такого рассмотрения связана с тем, что при диффузии в слабых растворах (т. е. при с< 1, когда только и применимо уравнение диффузии в форме (59,16)) частицы растворенного вещества практически не взаимодей­ствуют друг с другом, и потому можно рассматривать движе­ние каждой частицы независимо от других.

Пусть w(r,t)dr есть вероятность нахождения частицы в мо­мент времени t на расстоянии между г и г + dr от исходной точки. Полагая в (59,17) М/р = 1 и умножая на элемент объема 4nr²dr шарового слоя, получим:

™^(Г''^)аГ = 2ЧШ^е~^^ТгЧГ- ^(60Л)

Определим средний квадрат расстояния, на которое частица удалится от исходной точки в течение времени t. Имеем:

оо

г*= \г²хю{г, t)dr. (60,2)

о

Вычисление с помощью (60,1) дает

?=6Dt. (60,3)

Таким образом, среднее расстояние, проходимое частицей в те­чение некоторого интервала времени, пропорционально квадрат­ному корню из этого времени.

Коэффициент диффузии взвешенных в жидкости частиц мо­жет быть вычислен по их так называемой подвижности.

Предположим, что на эти частицы действует некоторая по­стоянная внешняя сила f (например, сила тяжести). В стацио­нарном состоянии сила, действующая на каждую частицу, долж­на уравновешиваться силой сопротивления, испытываемой дви­жущейся частицей со стороны жидкости. При не слишком боль­ших скоростях" сила сопротивления пропорциональна первой сте­пени скорости. Написав ее в виде v/b, где b — постоянная, и приравнивая внешней силе f, получим:

v = Ы, (60,4)

т. е. скорость, приобретаемая частицей под влиянием внешней

силы, пропорциональна этой силе. Постоянная Ь называется под­вижностью и может быть, в принципе, вычислена с помощью гидродинамических уравнений. Так, для частиц, имеющих форму шариков (радиуса R), сила сопротивления равна 6ят)^и (см. (20,14)), а потому подвижность

Для частиц не шарообразной формы сила сопротивления за­висит от направления движения; она может быть написана в виде dikVk, где ащ — симметрический тензор (см. (20,15)). При вычислении подвижности надо произвести усреднение по всем ориентациям частицы; если а\, ai, аг — главные значения сим­метрического тензора a_lk, то мы получим:

'--Hi+i+i)- «ад

Подвижность Ь связана с коэффициентом диффузии D про­стым соотношением. Для его вывода напишем диффузионный поток i, который содержит наряду с обычным членом —pDVc, связанным с градиентом концентрации (температуру предпола­гаем постоянной), также и член, связанный со скоростью, при­обретаемой частицей под влиянием внешних сил. Этот послед­ний член равен pcv = pcbi. Таким образом '):

i = —pDVc + pcbi. (60,7)

Перепишем это выражение в виде

^{i =} - (dSo_T,_p^Wli+pcbf'

где р. теперь — химический потенциал взвешенных частиц (иг­рающих роль растворенного вещества). Зависимость этого по­тенциала от концентрации (в слабом растворе) дается выра­жением

ц = Г1пс + гр(р, Т)

(см. V § 87), так что

i = — -^-Vp + рсМ.

В состоянии термодинамического равновесия диффузия отсут­ствует и поток i должен обращаться в нуль. С другой стороны, при наличии внешнего поля условие равновесия требует по­стоянства вдоль раствора суммы р+(7, где U — потенциальная энергия взвешенной частицы в этом поле. Тогда Vp = —V(7 = = —f и из равенства i = 0 получим

D = ТЬ. (60,8);

') Здесь с может быть определено как число взвешенных частиц в еди* нице массы жидкости, а i — как плотность потока числа этих частиц.

Это и есть искомое соотношение между коэффициентом диффу­зии и подвижностью (соотношение Эйнштейна).

Подставляя (60,5) в (60,8), найдем следующее выражение для коэффициента диффузии шарообразных частиц:

<⁶⁰'⁹>

Наряду с поступательным броуновским движением и посту­пательной диффузией взвешенных частиц можно рассмотреть их вращательное броуновское движение и диффузию. Анало­гично тому как коэффициент поступательной диффузии вычис­ляется через силу сопротивления, так коэффициент вращатель­ной диффузии может быть выражен через момент сил, действую­щих на вращающуюся в жидкости частицу.

Задачи

1. Частицы совершают броуновское движение в жидкости, ограниченной с одной стороны плоской стенкой; при попадании на стенку частицы «прили­пают» к ней. Определить вреоятность того, что частица, находящаяся в на­чальный момент времени на расстоянии хо от стенки, прилипнет к ней в те­чение времени t.

Дата добавления: 2014-11-07