Ol — V2X 45 страница

Решение. Распределение вероятностей w(x, t) (х — расстояние от стен­ки) определяется диффузионным уравнением с граничным условием w — 0 при 1 = 0 н начальным условием w = 6(х — х₀) при t = 0. Такое решение определяется формулой (52,4), в которой надо теперь писать w вместо Т, D вместо х ^и положить под знаком интеграла w₀ (х') = б (х' — х₀). Тогда получим:

w (x, t) = 1= \ ехр [ — -) — exp i — —=——) }.

2 s/я Dt X \ ADt J \ \Dt J J

Вероятность прилипания к стенке в единицу времени определяется значением диффузионного потока D dw/'dx при х = 0; искомая же вероятность W(t) прилипания в течение времени t равна

t

-/>C.f!L| J дх \х-о

и

Подставляя до, получим:

2. Определить порядок величины времени т, в течение которого взвешен­ная в жидкости частица поворачивается вокруг своей оси на большой угол.

Решение. Искомое время т определится как время, в течение которого частица при броуновском движении сместится на расстояние порядка вели­чины своих линейных размеров а. Согласно (60,3) имеем; т ~ a²/D, а соглас­но (60,9) D ~ Т/ца. Таким образом,

•па³

ГЛАВА VII

ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ

§ 61. Формула Лапласа

В этой главе мы изучим явления, происходящие вблизи по­верхности раздела между двумя сплошными средами (в дей­ствительности, конечно, соприкасающиеся тела разделены узким переходным слоем, который вследствие его весьма малой тол­щины можно рассматривать как поверхность).

Если поверхность раздела двух сред искривлена, то вблизи нее давления в обеих средах различны. Для определения этой разности давлений (называемой поверхностным давлением) на­пишем условие термодинамического равновесия обоих тел друг с другом с учетом свойств поверхности их раздела.

Пусть поверхность раздела подвергается бесконечно малому смещению. В каждой точке несмещенной поверхности проведем нормаль к ней. Отрезок нормали, заключенный между ее пере­сечениями с несмещенной и смещенной поверхностями, обозна­чим посредством б£. Тогда объем каждого элемента простран­ства, заключенного между поверхностями, есть 8t,df, где df — элемент поверхности. Пусть pi и р₂ — давления в первой и вто­рой средах и будем считать б£ положительным, если смещение поверхности раздела производится, скажем, в сторону второй среды. Тогда работа, которую надо произвести для описанного изменения объема, равна

\(-Pi + p₂)^df.

Полная работа 8R смещения поверхности получится путем прибавления сюда еще работы, связанной с изменением пло­щади самой этой поверхности. Эта часть работы пропорцио­нальна, как известно, изменению б/ площади поверхности и равна аб/, где а — поверхностное натяжение. Таким образом, полная работа равна

6fl = -$(_Pl-p₂)6£d/-r-_a5/. (61,1)

Условие термодинамического равновесия определяется, как из­вестно, обращением 8R в нуль.

Пусть далее Ri и R₂— главные радиусы кривизны в данной точке поверхности; мы будем считать R_x и R₂ положительными, если они направлены внутрь первой среды. Тогда элементы длины dli и dh на поверхности, проведенные в плоскостях ее главных сечений, получают при бесконечно малом смещении по­верхности приращения, равные соответственноЩ-dl_x и 4гdl₂(dl_x

AI А2

и dt₂ надо рассматривать как элементы дуги окружностей с радиусами Ri и R₂). Поэтому элемент поверхности df = dl\dl₂ будет равен после смещения

"■О +£)*(' +f.)-*.«я.О +%+%)■

т. е. изменится на величину

(i + i).

Отсюда видно, что полное изменение площади поверхности раз­дела есть

Подставляя полученные выражения в (61,1) и приравнивая нулю, получим условие равновесия в виде

S6_S{(p₁-p₂)-a(^+^)}d/ = 0.

Это условие должно выполняться при произвольном бесконечно малом смещении поверхности, т. е. при произвольном б£. По­этому необходимо, чтобы стоящее под интегралом в скобках выражение тождественно обращалось в нуль, т. е.

л-л=«(т?Г ⁺ Т5-)- <⁶¹'³>

Это и есть формула (формула Лапласа), определяющая по­верхностное давление¹). Мы видим, что если R\ и R₂ положи­тельны, то р\ > р₂. Это значит, что.из двух тел давление боль­ше в том, поверхность которого выпукла. Если Ri=R₂z= со, т. е. поверхность раздела плоская, то давления в обоих телах, как и должно было быть, одинаковы.

Применим формулу (61,3) для исследования механического равновесия соприкасающихся тел. Предположим, что ни на по­верхность раздела, ни на сами тела не действуют никакие внеш­ние силы. Тогда вдоль каждого из тел давление постоянно. Имея в виду формулу (61,3), мы можем поэтому написать условие равновесия в виде

± + const (61,4)

') Изложенный вывод отличается от данного в V, § 156, по существу, лишь тем, что здесь рассматривается поверхность раздела произвольной формы, а не только сферической.

Таким образом, сумма обратных радиусов кривизны должна быть постоянной вдоль всей свободной поверхности раздела. Если вся поверхность свободна, то условие (60,4) означает, что поверхность должна иметь шарообразную форму (например, по­верхность маленькой капли, влиянием силы тяжести на которую можно пренебречь). Если же поверхность закреплена вдоль ка­кой-нибудь линии (например, у жидкой пленки на твердой рам­ке), то ее форма является более сложной.

В применении к равновесию тонких пленок жидкости, закреп­ленных на твердой рамке, в условии (61,4) справа должен стоять нуль. Действительно, сумма \/R\ + l/i?2 должна быть одинако­вой вдоль всей свободной поверхности пленки и в то же время на двух своих сторонах она должна иметь противоположный знак, поскольку если одна сторона выпукла, то другая вогнута с теми же радиусами кривизны, которые, однако, должны счи­таться теперь отрицательными. Отсюда следует, что условие рав­новесия тонкой пленки есть

Рассмотрим теперь условие равновесия на поверхности тела, находящегося в поле тяжести. Предположим для простоты, что второй средой является просто атмосфера, давление которой на протяжении размеров тела можно считать постоянным. В каче­стве самого тела рассмотрим несжимаемую жидкость. Тогда имеем р2 = const, а давление pi в жидкости равно согласно (3,2) pi = const — pgz (координата z отсчитывается вертикаль­но вверх). Таким образом, условие равновесия приобретает вид

7^+7^ + ^ z = const (61,6)

Надо, впрочем, отметить, что для определения равновесной формы поверхности жидкости в конкретных случаях обычно бы­вает удобным пользоваться условием равновесия не в виде (61,6), а непосредственно решая вариационную задачу о мини­муме нолной свободной энергии. Внутренняя свободная энергия жидкости зависит только от объема, но не от формы поверх­ности. От формы зависит, во-первых, поверхностная свободная энергия

И

и, во-вторых, энергия во внешнем поле (поле тяжести), равная

gp J z dV.

Таким образом, условие равновесия можно написать в виде

a \ df + gp^zdV= min. (61,7)

Определение минимума должно производиться при дополнитель­ном условии

dV = const,

(61,8)

выражающем неизменность полного объема жидкости.

Постоянные а, р, g входят в условия равновесия (61,6—7)

только в виде отношения. Это отношение имеет размерность

квадрата длины. Длину

(61,9)

называют капиллярной постоянной¹). Форма поверхности жид­кости определяется только этой величиной. Если капиллярная постоянная велика (по сравнению с размерами тела), то при определении формы поверхности можно пренебречь полем тя­жести.

Для того чтобы определить из условия (61,4) или (61,6) фор­му поверхности, надо иметь формулы, определяющие радиусы кривизны по форме поверхности. Эти формулы известны из диф­ференциальной геометрии, но имеют в общем случае довольно сложный вид. Они значительно упрощаются в том случае, когда форма поверхности лишь слабо отклоняется от плоской. Мы вы­ведем здесь соответствующую приближенную формулу непосред­ственно, не пользуясь общей формулой дифференциальной гео­метрии.

Пусть г = t,(x, у)— уравнение поверхности; мы предполагаем, что £ везде мало, т. е. что поверхность слабо отклоняется от плоскости z = 0. Как известно, площадь f поверхности опреде­ляется интегралом

'-W¹+(£)'+($)'"*•

или приближенно при малых Х>

'-$['+К£)^,+Н£)>*-

(61,10)

Определим вариацию Ц:

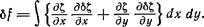
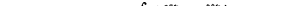Интегрируя по частям, находим:

Сравнив это выражение с (61,2), получаем:

*+*—(£+£)• «".">

Это и есть искомая формула, определяющая сумму обратных радиусов кривизны слабо изогнутой поверхности.

При равновесии трех соприкасающихся друг с другом фаз их поверхности раздела устанавливаются таким образом, чтобы была равна нулю равнодействующая трех сил поверхностного натяжения, действующих на общую линию соприкосновения трех сред. Это условие приводит к тому, что поверхности раздела должны пересекаться друг с другом под углами (так называе­мые краевые углы), определяющимися значениями поверхност­ного натяжения.

Наконец, остановимся на вопросе о граничных условиях, ко­торые должны соблюдаться на границе двух движущихся жид­костей при учете сил поверхностного натяжения. Если поверх­ностное натяжение не учитывается, то на границе двух жидко­стей имеем:

что выражает равенство сил трения, действующих на поверхно­сти обеих жидкостей. При учете поверхностного натяжения надо написать в правой части этого условия дополнительную силу, определяемую по величине формулой Лапласа и направленную по нормали к поверхности:

n_ko% -»_fto$ = а (-1- 4- J-) я.. (61,12)

Иначе можно написать это уравнение в виде

(Pi ~ Рг) *t = М - °'%) ^пь + ^а{-Щ+ж) (61.13)

Если обе жидкости можно считать идеальными, то вязкие напря­жения oh исчезают, и мы получаем вновь простое уравнение (61,3).

Условие (61,13), однако, еще не является наиболее общим. Дело в том, что коэффициент поверхностного натяжения а мо­жет оказаться не постоянным вдоль поверхности (например, в результате непостоянства температуры). Тогда наряду с нор­мальной силой (исчезающей в случае плоской поверхности) по­является некоторая дополнительная сила, направленная танген­циально к поверхности. Аналогично тому как при неравномер­ном давлении появляется объемная сила, равная (на единицу объема) — Vp здесь имеем для тангенциальной силы it, действую­щей на единицу площади поверхности раздела, f< = grada. Мы пишем здесь градиент со знаком плюс перед ним, а не со знаком

минус, как в силе — Vp, в связи с тем, что силы поверхно­стного натяжения стремятся уменьшить площадь поверхности, между тем как силы давления стремятся увеличить объем тела. Прибавляя эту силу к правой стороне равенства (61,13), полу­чим граничное условие

[л-р*-^аЫг+i)]ⁿ<⁼(^а'<*" ⁰"<*)^п*+St^(61Л4)

(единичный вектор нормали п направлен внутрь первой жид­кости). Отметим, что это условие может быть выполнено только у вязкой жидкости. Действительно, у идеальной жидкости a'_ik — 0; тогда левая сторона равенства (61,14) будет представ­лять собой вектор, направленный по нормали, а правая — век­тор, направленный по касательной к поверхности. Но такое ра­венство невозможно (за исключением, разумеется, тривиального случая, когда эти величины равны нулю каждая в отдельности).

Задачи

1. Определить форму жидкой пленки, края которой закреплены на двух
рамках, имеющих форму окружностей, центры которых лежат на общей пря-
_zмой, перпендикулярной к их плоскостям (разрез плен-

7Й ки изображен на рис. 41).

Решение. Задача сводится к отысканию поверх­ности минимальной площади, образованной вращением вокруг прямой т — О кривой z = z (г), имеющей концы в двух заданных точках А и В. Площадь поверхности вращения есть

2г

/ = 2я jj F (г, г') dz, F = r(l + г'²)¹¹².

■■ const.

где г' = dr/dz. Первый интеграл уравнения Эйлера за­дачи о минимуме такого интеграла (с выражением F, не содержащим z) есть

дг'

dF

F-r'

В данном случае это дает:

Г = Сх (1 + г'²)1/2, откуда находим после интегрирования

г = ci ch -

■ с₂

таким образом, искомая поверхность является поверхностью, образованной вращением цепной линии (так называемый катеноид). Постоянные Ci и с₂ должны быть определены так, чтобы кривая r(z) проходила через заданные точки А и В. При этом с₂ зависит просто от выбора начала координат на оси z. Для постоянной же Ci получаются два значения, из которых должно быть выбрано большее (меньшее не соответствует минимуму интеграла).

При увеличении расстояния к между рамками при некотором определен­ном его значении наступает момент, когда уравнение, определяющее постоян­

ную Си перестает иметь вещественные корн». При больших расстояниях устойчивой является только форма, соответствующая двум пленкам, натяну­тым на каждую из двух рамок. Так, для двух рамок одинакового радиуса R катеноидная форма становится невозможной при расстоянии h между рамка­ми, равном h = 1,33/?.

2. Определить форму поверхности жидкости, находящейся в поле тяже­сти и соприкасающейся с одной стороны с вертикальной плоской стенкой. Краевой угол, образуемый жидкостью при соприкосновении с веществом стенки, равен 9 (рис. 42).

Решение. Выбираем оси координат указанным на рис. 42 образом. Плоскость х = 0 есть плоскость стенки, а z = 0 есть плоскость поверхности жидкости вдали от стенки. Радиусы кривизны поверхности г = z(x):

#, = 00, R₂ = ~

(1 + г'²)³'²

так что уравнение (61,6) приобретает вид
2z z"

= const

(1 + г'²)*²

(1)

X

Рис. 42

(a — капиллярная постоянная). При x — оо должно быть z = 0, l/Rz = 0; поэтому const = 0. Первый интеграл получающегося уравнения есть

У1 +

Л ^А а²

(2)

Из условия на бесконечности (г =■ 0, г' = 0 при * = оо) имеем А = 1. Вто­рое интегрирование дает

V2

а., а л/2~. /„ z².

■=■ Arch —---- Мл/2--------- Ь*о-

i2 z У а²

Постоянная х₀ должна быть определена так, чтобы на поверхнос ти стенки (х = 0) было z' = —ctg 9 или согласно (2) z = h, где h — а V1 — sin 9 есть высота поднятия жидкости у самой стенки.

3. Определить форму поверхности жидкости, поднявшейся между двумя вертикальными парал­лельными плоскими пластинками (рис. 43).

х

Рис. 43

Решение! Выбираем плоскость у, z посредине между обеими пластинками, а плоскость х, у — совпадающей с поверхностью жидкости вне про­странства между пластинками, вдали от них. В урав­нении (1) задачи 2, выражающем условие равно­весия и потому справедливом вдоль всей поверхно­сти жидкости (как между, так и вне пластинок), условия при х = оо дают опять const = 9. В инте­грале же (2) уравнения (1) постоянная А различна

для |*| > d/2 и |*| < d/2 (при |*| = d/2 функция z(x) имеет разрыв). Для пространства между пластинками имеем следующие условия: при х =*• О должно быть г' = 9, а при * = d/2 г' = ctg 9, где 9 — краевой угол, Со­гласно (2) имеем для высот zo = z(0) и z» = z(d/2);

Интегрируя (2), получаем:

а Г cos | rig

где g— новая переменная, связанная с г посредством г = ал/А—cos |. Этот интеграл — эллиптический и не может быть выражен в элементарных функциях. Постоянная А определяется из условия z = z₄ при х = d/2, от­куда

cos | dl

УЛ — cos §

Полученные формулы определяют форму поверхности жидкости в простран­стве между пластинками. При d-*-Q А стремится к бесконечности. Поэтому при d <С а имеем:

4-в

d ж ^а ■ \ cos £ d\ = —т=г cos В,
Ул J УЛ

откуда A — (a/d)²cos²8. Высота поднятия жидкости

г₀» z\ «-J- cos 6;

эта формула может быть получена, разумеется, и элементарным путем.

4. На плоскости горизонтальной твердой поверхности находится (в поле тяжести) тонкий неравномерно нагретый слой жидкости; ее температура яв­ляется заданной функцией координаты х вдоль слоя, причем (благодаря тон­кости пленки) ее можно считать не зависящей от координаты z вдоль тол­щины слоя. Неравномерная нагретость приводит к возникновению стационар­ного движения жидкости в пленке, в результате чего ее толщина £, будет меняться вдоль слоя; требуется определить функцию С == £(*) •

Решение. Вместе с температурой заданными функциями х являются также плотность р жидкости и поверхностное натяжение а. Давление в жид­кости p — po + pg(t, — z), где ро — атмосферное давление (давление на сво­бодной поверхности слоя); изменением давления благодаря искривлению по­верхности можно пренебречь. Скорость жидкости в тонком слое можно счи­тать направленной везде вдоль оси х. Уравнение движения гласит:

⁴ дг² дх П dx ² dx]' ^(l)

На твердой поверхности (г = 0) имеем v = 0, а на свободной поверхности (г = £) должно выполняться граничное условие (61,14), которое в данном случае дает

dvda

¹¹ dz z=£^_ dx '

Интегрируя уравнение (1) с этими условиями, получим:

(₉ z \ d (р£) gz.„„,,. dp da...

Ввиду стационарности движения полный поток жидкости через попереч­ное сечениз слоя должен быть равен нулю: ^ v dz = 0. Подставляя сюда (2),

о

получим следующее уравнение:

р dt,² 1 dp _g2 _ 1 da

3~ dx ⁺ 4 ⁶ ~ g dx' определяющее функцию £,{*)■ Интегрируя его, получим:

g£² = 3p-³'⁴[$ р-¹'⁴da + const]. (3)

Если температура (а с ней и р и а) лишь мало меняется вдоль слоя жидкости, то можно написать (3) в виде

^•(fr+^<«-«•>.

где £о — значение £ в точке, где р = р₀, а = а₀.

§ 62. Капиллярные волны

Поверхность жидкости стремится принять свою равновесную форму как под влиянием действующего на жидкость поля тя­жести, так и под влиянием сил поверхностного натяжения. Ме­жду тем при изучении в § 12 волн на поверхности жидкости мы не учитывали этого последнего фактора. Мы увидим ниже, что влияние капиллярности на гравитационные волны существенно при малых длинах волн.

Как и в § 12, будем предполагать амплитуду колебаний ма­лой по сравнению с длиной волны. Для потенциала скорости имеем по-прежнему уравнение

Дср = 0.

Условие же на поверхности жидкости будет теперь иным: раз­ность давлений с обеих сторон этой поверхности должна быть равной не нулю, как это предполагалось в § 12, а должна опре­деляться формулой Лапласа (61,3)

Обозначим г-координату точек поверхности жидкости посред­ством £. Поскольку t, мало, то можно воспользоваться выраже­нием (61,11) и написать формулу Лапласа в виде

"^WJ"

Здесь р есть давление в жидкости вблизи поверхности, р₀ — по­стоянное внешнее давление. Для р подставляем согласно (12,2)

dtp

и находим:

Р = — Р£$ - Р - _dt

рй + р£-«(0 + $) = о

(по тем же причинам, как и в § 12, можно, определяя соответ­ствующим образом ф, опустить постоянную р₀). Продифферен­цировав это соотношение по t и заменив в нем dt,/dt на ду/дг, получим граничное условие для потенциала <р в виде

{■*£+р-$"-£(&+#)Ь-^{л (ад}

Рассмотрим плоскую волну, распространяющуюся вдоль оси х. Как и в § 12, получаем решение в виде

• ф = Ае^кг cos (kx — юг).

Связь между k и и определяется теперь из предельного усло­вия (62,1) и имеет вид

<o² = gk+fk³ (62,2)

(W. Thomson, 1871).

Мы видим, что при больших длинах волн, удовлетворяющих условию k <С (gp/a)^1/2 или

(а — капиллярная постоянная), влиянием капиллярности можно пренебречь, и волна является чисто гравитационной. В обрат­ном случае коротких волн можно пренебречь влиянием поля тя­жести. Тогда

ш² = -^³. (62,3)

Такие волны называются капиллярными; в промежуточном слу­чае говорят о капиллярно-гравитационных волнах.

Определим еще собственные колебания сферической капли несжимаемой жидкости совершаемые ею под влиянием капил­лярных сил. При колебаниях происходит отклонение формы по­верхности капли от сферической. Амплитуду колебаний будем, как обычно, предполагать малой.

Начнем с определения суммы l/R\ + \/R₂ для поверхности, слабо отклоняющейся от сферической. Поступим для этого ана­логично тому, что мы делали при выводе формулы (61,11) Пло­щадь поверхности, описываемой в сферических координатах¹) г, Э, ф функцией г = г(0, ф), равна, как известно, интегралу

Н5л/*+Ш*+1^(%)*^г*^ша'^а*-^(62,4)

о о

*) Ниже в этом параграфе ф обозначает азимут сферических координат, а потенциал скорости мы будем обозначать посредством ф.

Шаровая поверхность описывается уравнением г = const = R (R-^-радиус шара), а близкая к ней поверхность — уравнением r = R-\-Z, с малым %. Подставляя это в (62,4), имеем прибли­женно

2я я

MS{«+tf+T[(§ У+(Щ-•

о о

Определим изменение б/ поверхности при варьировании £. Имеем:

2я я О О

Интегрируя второй член по частям по углу 6, а третий член — по ф, получаем:

2я Я

б/ = $ 5 {2 (* + О - sin 0§) - -^||} б£зШвЛйф.

о о

Если разделить выражение в фигурных скобках на R(R-j-21), то выражение, которое будет стоять под знаком интеграла в ка­честве множителя при

в£ df «6ZR (R + 21) sin 0 dQ dtp,

будет согласно формуле (61,2) представлять собой как раз ис­комую сумму обратных радиусов кривизны, вычисленную с точ­ностью до членов первого порядка по £. Таким образом, по­лучим:

*Н-т-*-*Ь^#+-™(*^вЗ-)Н««>.

Первый член соответствует чисто сферической поверхности, для которой Ri—R2 = R.

Потенциал скорости гр удовлетворяет уравнению Лапласа Дтр = 0 с граничным условием при г = R, имеющим вид (анало­гично тому, что мы имели для плоской поверхности)

р*+«{т-*-т[-ЬяМ)+-а^$]}+^-

Постоянную 2а/# + Ро в этом условии снова можно опустить; дифференцируя по времени и подставляя

dt, „

находим окончательно граничное условие для ф в виде

Будем искать решение в виде стоячей волны * = (г, 6, ф),

где функция / удовлетворяет уравнению Лапласа А/ = 0. Как известно, всякое решение уравнения Лапласа может быть пред­ставлено в виде линейной комбинации так называемых объем­ных шаровых функций вида

r^lY_lm(Q, ф),

где Yim(Q, ф) — шаровые функции Лапласа, равные Ушф, <p) = P?*(cos6)e""*.

Здесь

, '. d^mP, (cos 9)

присоединенная функция Лежандра (/'/(cos8) — полином Ле«жандра /-го порядка). Как известно, / пробегает все целые по­ложительные значения, включая нуль, а т пробегает при за­данном / значения т = 0, ±1, ±2,..., ±1.

Соответственно этому ищем частное решение поставленной задачи в виде

•ф = Ае~^шг¹Р™ (cos 6) е^1т». (62,7)

Частота со определяется так, чтобы удовлетворить предельному условию (62,6). Подставляя в это уравнение выражение (62,7) и воспользовавшись тем, что шаровые функции Yim удовлетворяют уравнению

находим (сокращая общий множитель \f>):

рш² + -^{2-/(/+1)} = 0,

откуда

<о²=-^/а-1)(/ + 2). (62,8)

{Rayleigh, 1879).

Эта формула определяет частоты собственных капиллярных колебаний сферической капли. Мы видим, что они зависят толь­ко от числа /, но не от т. Между тем данному / соответствует 22+1 различных функций (62,7). Таким образом, каждая из частот (62,8) соответствует 2/+1 различным собственным ко­лебаниям. О независимых собственных колебаниях, имеющих одинаковые частоты, говорят как о вырожденных; в данном слу­чае имеет место 2/+ 1-кратное вырождение.

Выражение (62,8) обращается в нуль при 1 = 0 и при / = 1. Значение / = 0 соответствовало бы радиальным колебаниям, т. е. сферически симметричным пульсациям капли; в несжимае­мой жидкости такие колебания, очевидно, невозможны. При / = 1 движение представляло бы собой поступательное переме­щение капли как целого. Наименьшая возможная частота ко­лебаний капли соответствует 1 = 2 и равна

<ь=-&- (62.9)

Задачи

1. Определить зависимость частоты от волнового вектора для капилляр-
но-гравитационных волн на поверхности жидкости, глубина которой равна п.

Решение. Подставляя в условие (62,1)

Ф = A cos (kx — tor) ch k (z + h) (см. задачу 1 § 12), получаем:

со² =(gfe+ ££!-) _th kh.

При kh > 1 мы возвращаемся к формуле (62,2), а для длинных волн (йА<1) имеем:

2. Определить коэффициент затухания капиллярных волн.
Решение. Подставляя (62,3) в (25,5), получим

_ 2r|fe² _ 2т|со^4/3

р^1/3а²'³ '

3. Найти условие устойчивости тангенциального разрыва в поле тяжести с учетом поверхностного натяжения; жидкости по обе стороны поверхности разрыва предполагаются различными (Kelvin, 1871).

Решение. Пусть U — скорость верхнего слоя жидкости относительно нижнего. Накладываем на основное движение периодическое вдоль горизон­тальной оси возмущение и ищем потенциал скорости в виде;

в нижней жидкости

ф = Ae^kz cos (kx — cor)

и в верхней

ф' = A'e~^kz cos (kx - cor) + Vx.

Для нижней жидкости имеем на поверхности разрыва

_ <5ф dl

(£ — вертикальная координата поверхности раздела), а в верхней

„' _ -г; д£ | д£

* ^— dz ~ дх dt ■

Условие равенства давлений в обеих жидкостях на поверхности разрыва имеет вид

(при раскрытии выражения»'* — U^z должны быть сохранены только члены первого порядка по А'). Смещение £ ищем в виде £ = a sin (ft*—сог). Под­ставляя <р, ф', £ в написанные три условия при 2 = 0, получаем три уравне­ния, исключая из которых о, А, А', находим:

и P'U | Г kg (р - pQ k'pp'U* ak' 11/2

P + P' ^±L Р + Р' (р + р')^{2 +} P + p'J '

Для того чтобы это выражение было вещественным при всех k, необходимо выполнение условия

_с,_{4 <} 4ag (о - р') (р + р'П РУ²

В противном случае существуют комплексные ш с положительной мнимой частью и движение неустойчиво.

§ 63. Влияние адсорбированных пленок на движение жидкости

Наличие на поверхности жидкости пленки адсорбированного ею вещества может существенно изменить гидродинамические свойства свободной поверхности жидкости. Дело в том, что при изменении формы поверхности, сопровождающем движение жид­кости, происходит растяжение или сжатие пленки, т. е. измене­ние поверхностной концентрации адсорбированного вещества. Эти изменения приводят к появлению дополнительных сил, ко­торые и должны быть учтены в граничных условиях, имеющих место на свободной поверхности жидкости.

Мы ограничимся здесь рассмотрением адсорбированных пле­нок веществ, которые можно считать нерастворимыми в самой жидкости. Это значит, что вещество находится только у поверх­ности и не проникает в глубь жидкости. Если же поверхностно-активное вещество обладает также и некоторой заметной рас­творимостью, то необходимо было бы принять во внимание про­цессы диффузии этого вещества между поверхностной пленкой и объемом жидкости, возникающие при изменении концентра­ции плёнки.

Дата добавления: 2014-11-07