Ol — V2X 51 страница

Будем предполагать, что длина волны звука X велика по сравнению с размерами / тела; тогда для вычисления рассеян­ной волны можно воспользоваться формулами (74,8) и (74,11)'). Рассеянную волну мы при этом рассматриваем как волну, излу­чаемую телом; разница заключается только в том, что вместо

') В то же время требуется, чтобы размеры тела были велики по сравне­нию с амплитудой смещений частиц жидкости в волне; в противном случав: движение жидкости не будет, вообще говоря, потенциальным.

движения тела в жидкости мы имеем теперь дело с движением жидкости относительно тела. Обе задачи, очевидно, эквива­лентны.

Для потенциала излучаемой волны мы получили выражение

₌ V Аг_

^ Ляг¹ сг²

В этой формуле V было объемом тела. Теперь же объем самого тела остается неизменным, и под V надо подразумевать не ско­рость изменения объема тела, а то количество (объем) жидг-кости, которое вошло бы в единицу времени в объем, занимае­мый телом (этот объем обозначим посредством Vo), если бы этого тела вообще не было. Действительно, при наличии тела это количество жидкости не проникает внутрь занимаемого те­лом объема, что эквивалентно выбрасыванию этого же количе­ства из объема Vo- Коэффициент же при 1/4яг в первом члене в ф должен быть, как мы видели в предыдущем параграфе, равен как раз количеству «выбрасываемой» в 1 сек. из начала координат жидкости. Это количество легко вычислить. Измене­ние массы жидкости в единицу времени в объеме, равном объ­ему тела, равно У₀р, где функция р определяет изменение со временем плотности жидкости в падающей звуковой волне (по­скольку длина волны велика по сравнению с размерами тела,, то на протяжении расстояний порядка этих размеров плотность р можно считать постоянной; поэтому мы можем писать изменение массы жидкости в объеме Уо просто в виде У₀р, где р одинаково вдоль всего объема У₀). Изменение объема жидкости, соответ­ствующее изменению массы р У₀, есть, очевидно, Voip/р. Таким образом, вместо У надо писать в выражении для ф величину Уор/р. В падающей плоской волне переменная часть плотности р' связана со скоростью посредством р' = pv/c; поэтому р = = р' = pv/c, и вместо Уор/р можно писать Vqv/c.

Что касается вектора А, то при движении тела в жидкости он определяется формулами (11,5—6):

4прЛ; = mikUk + pVolli.

Теперь же мы должны писать вместо скорости и тела взятую с обратным знаком скорость v жидкости в падающей волне (ко­торую она имела бы в месте нахождения тела, если бы тела вовсе не было). Таким образом,

Окончательно получаем для потенциала рассеянной волны с вектором А, определяющимся формулой (78,1). Для распреде­ления скоростей в рассеянной волне получаем отсюда:

*р=^ + ^ (78,3)

(см. § 74; п — единичный вектор в направлении рассеяния).

Среднее количество рассеиваемой (в 1 с.) в данном элементе do телесного угла энергии определяется потоком энергии, рав­ным cpv² do. Полная интенсивность /_р рассеяния получается ин­тегрированием этого выражения по всем направлениям. При этом интегрировании удвоенное произведение обоих членов в (78,3), пропорциональное первой степени косинуса угла между Направлением рассеяния и направлением распространения па­дающей волны, исчезает и остается (ср. (74,10) и (74,13)):

¹р^ж=ЩГ^+-^-^К' (78,4)

Рассеяние принято характеризовать его эффективным сече­нием (или просто сечением) da. Оно определяется как отноше­ние средней (по времени) рассеиваемой в данном элементе те­лесного угла энергии к средней плотности потока энергии в па­дающей волне. Полное сечение а равно интегралу от do по всем направлениям рассеяния, т. е. равно отношению полной интен­сивности рассеяния к плотности падающего потока энергии. Се­чение имеет, очевидно, размерность площади.

Средняя плотность потока энергии в падающей волне есть
cpv². Поэтому дифференциальное сечение рассеяния равно от-
ношению _

da = -с|. г² do. (78,5)

Полное сечение равно

Vl v² An А²

Для монохроматической падающей волны среднее значение квадрата второй производной от скорости по времени пропор­ционально четвертой степени частоты. Таким образом, сечение рассеяния звука телом, размеры которого малы по сравнению с длиной волны, пропорционально четвертой степени частоты.

Наконец, остановимся коротко на обратном предельном слу­чае, когда длина волны рассеиваемого звука мала по сравнению с размерами тела. В этом случае все рассеяние, за исключением лишь рассеяния на очень малые углы, сводится к простому от­ражению от поверхности тела. Соответствующая часть полного сечения рассеяния равна, очевидно, просто площади S сечения тела плоскостью, перпендикулярной к направлению падающей волны. Рассеяние же на малые углы (углы порядка 'к/1) пред­ставляет собой дифракцию от краев тела. Мы не станем излагать здесь теорию этого явления, полностью аналогичную теории ди­фракции света (см. II §§ 60, 61). Укажем лишь, что согласно принципу Бабине полная интенсивность дифрагировавшего звука равна полной интенсивности отраженного звука. Поэтому ди­фракционная часть сечения рассеяния равна той же площади S, а полное сечение равно, следовательно, 2S.

Задачи

1. Определить сечение рассеяния плоской звуковой волны твердым шари­ком, радиус R которого мал по сравнению с длиной волны.

Решение. Для скорости в плоской волне имеем v — a cos at (в дан­ной точке пространства). Вектор А равен в случае шара (см. задачу 1 § 11) А = —vR³/2. Для дифференциального сечения получаем:

ю⁴/?⁸ /, 3 cos 9 У,

(0 — угол между направлением падающей волны и направлением рассеяния). Интенсивность рассеяния максимальна в направлении 6 = я, противополож­ном направлению падения. Полное сечение равно

7я (R³a² у

Здесь (а также ниже в задачах 3, 4) предполагается, что плотность р₀

шарика велика¹ по сравнению с плотностью р газа; в противном случае надо учитывать увлечение шарика действующими на него со стороны колеблюще­гося газа силами давления.

2. Определить сечение рассеяния звука жидкой каплей с учетом сжимае­мости жидкости и движения капли под влиянием падающей волны.

----- 2 ^CP^V Ро^со

Решение. При адиабатическом изменении давления газа, в котором находится капля, на величину р' объем капли уменьшается на

V₀

l2-(*£\ р':

Ро V ^дР)s

(р — плотность газа, р₀ — плотность жидкости в капле, с₀ — скорость звука в жидкости). В выражениях (78,2—3) надо писать теперь вместо Vav/c раз­ность

V₀ (б/с — йср/сор₀).

Далее, в выражении для А надо писать теперь вместо —v разность u — v, где и — скорость тела, приобретаемая им под влиянием падающей волны. Для шара получаем с помощью результатов задачи 1 § 11

2Р0 + Р

Подстановка этих выражений приводит к сечению

da='^-—i(1 - ^Р-Л - 3 cos 9 *=*Л* do.
9c IV ^coPo J Spo-г-р/

К, с²Р V ■ 3 (ро - р)² "J 4» J (2ро + р)² Г

Полное сечение равно

4ш>⁴/?⁹ (Y, с²р у, 3 (ро - р)²

9,"

3. Определить сечение рас сеян ия звука твердым шариком, радиус R ко­торого мал по сравнению с л/v/w. Теплоемкость шарика предполагается на­столько большой, что его температуру можно считать неизменной.

Решение. В этом случае должно быть учтено влияние вязкости газа на движение шарика, и векто р А должен быть видоизменен указанным в за­даче 2 § 74 образом; при R •уш/'У ■< 1 имеем:

2м

3Rv

А = - i ■

Кроме того, к рассеянию того же порядка величины приводит теплопро-
водность газа. Пусть Т_ае~^1(л( — колебания температуры в заданной точке
.звуковой волны. Распределение температуры вблизи шарика будет (ср. за-
дачу 2 § 52):

Г' - 7^-«{l - -f ехр [- (1 - 0 (г - R) д/^]}

(при г = R должно быть V — 0). Колич еств о тепла, передаваемое в единицу времени от газа к шарику, есть (при R л/ю/х^ l):

dr

"Передача этого тепла приводит к изменению объема газа, которое можно воспринимать в смысле его влияния на рассеяние как соответствующее эффек­тивное изменение объема шарика, равное

V = - 4я./?хвг;_е-Ш _ ~^Г~У< (Y — 1) о.

где р⁴—коэффициент теплового расширения газа, а у — c_p/c_v; мы воспользо­вались также формулами (64,13) и (79,2).

Учитывая оба эффекта, получим дифференциальное сечение рассеяния^:

г

со²/?² Г, 3.Л*

da = _с4 |х (Y - 1) - v cos 9J do.

Полное эффективное сечение:

4яа>²/?²

[x²(Y-D²+-f-^v2]-

Эти формулы применимы лишь постольку, поскольку стоксова сила тре­ния мала по сравнению с инерционными силами, т. е. r\R <С Мю, где М =.= 4я#³р₀/3 — масса шарика; в противном случае становится существенным увлечение шарика вязкими силами.

4. Определить среднюю силу, действующую на твердый шарик, рассеи­вающий плоскую звуковую волну (к ~> R).

Решение. Передаваемый в единицу времени от падающей волны ша­рику импульс, т. е. искомая сила, равен разности импульса, приносимого рас­сеиваемой волной, и полного потока импульса в рассеянной волне. Из падаю­щей волны рассеивается поток энергии, равный асЕ₀, где Е₀ — плотность

ЗВУК

pvt. VIII

энергии в падающей волне; соответствующий поток импульса получается деле­нием на с, т. е. равен оЕи. В рассеянной волне поток импульса в телесном угле do равен E_er²do = E<,do; проектируя его на направление распростране­ния падающей волны (очевидно, что искомая сила имеет это направление)

щая на шарик сила равна

и интегрируя по всем углам, получим Е_в J cos 9 da. Таким образом, действую-

F = E₀ ^ (1 — cos 9) da.

Подставляя сюда da из задачи 1, получим:

_ -s 11я<о⁴#^в

§ 79. Поглощение звука

Наличие вязкости и теплопроводности приводит к диссипа­ции энергии звуковых волн, в связи с чем звук поглощается, т. е. его интенсивность постепенно уменьшается. Для вычисления дис-сипируемой в единицу времени энергии £_мех воспользуемся сле­дующими общими соображениями. Механическая энергия пред­ставляет собой не что иное, как максимальную работу, которую можно получить при переходе из данного неравновесного состоя­ния в состояние термодинамического равновесия. Как известно из термодинамики, максимальная работа совершается, если пе­реход происходит обратимым образом (т. е. без изменения эн­тропии), и равна соответственно этому

Е_Мех ^=:х Eq — Е (S),

где Ео есть заданное начальное значение энергии тела в исход­ном состоянии, a E(S) — энергия тела в состоянии равновесия С той же энтропией S, которую тело имело вначале. Дифферен­цируя по времени, получаем:

дЕ ■

^Еыех = — Е (S) = —S-

Производная от энергии по энтропии есть температура. Поэтому

ар

— температура, которую имело бы тело, если бы оно находи­лось в состоянии термодинамического равновесия (с заданным значением энтропии). Обозначая эту температуру как Го, имеем,, следовательно:

Воспользуемся для 5 выражением (49,6),включающим в себя возрастание энтропии, обусловленное как теплопроводностью, так и вязкостью. Поскольку температура Т мало меняется вдоль жидкости и мало отличается от То, то можно вынести ее из-под знака интеграла и писать Т вместо Т₀:

-£,\(divx)²dV. (79,1)

Эта формула представляет собой обобщение формулы (16,3) на случай сжимаемой жидкости и наличия теплопроводности.

Пусть ось х совпадает с направлением распространения зву­ковой волны. Тогда

v_x = Vocos{kx — (at), v_y — Vz = 0. Два последних члена в (79,1) дают

- (4 Ч + ОJ№У^ = ~ *² (у Л + С) *5 $ sin² (ft* - со/) dK.

Нас, конечно, интересует среднее по времени значение величин; усреднение дает

(Vo — объем жидкости).

Далее, вычислим первый член в (79,1). Отклонение Т тем­пературы в звуковой волне от своего равновесного значения свя­зано со скоростью формулой (64,13), так что градиент темпера­туры равен

дТ. сТ dv всГ,...

■ът^вР1717 = - V ^{щк п {кх} ~ ^ш)-

Для среднего по времени значения от первого члена в (79,1) лолучаем:

КС²Т$² 2Д,2Т/

-С помощью известных термодинамических формул

с_р-с₀ = Гр² (f.), = ГР² ^ (|-Х = Г_Р V -g- (79,2)

.можно переписать это выражение в виде

2\с₀ c_p)^{R и}о^о-

Собирая полученные выражения, находим среднее значение диссипации энергии в виде

= - [(± г, + с) + - От - ^)] • (79,3)

Полная же энергия звуковой волны равна

E = ^V₀. (79,4)

Введенный в § 25 коэффициент затухания волны определяет-закон уменьшения интенсивности со временем. Для звука, од­нако, обычно приходится иметь дело с несколько иной поста­новкой задачи, в которой звуковая волна распространяется вдоль жидкости и ее интенсивность падает с увеличением прой­денного расстояния х. Очевидно, что это уменьшение будет про­исходить по закону е~²ч^х, а для амплитуды — как е~"*^х, где коэф­фициент поглощения у определяется посредством

(79,5)

2сЕ

Подставляя сюда (79,3) и (79,4), находим, таким образом, сле­дующее выражение для коэффициента поглощения звука:

*-£[(!••+О+»(£-£)]-»²- рад

Отметим, что он пропорционален квадрату частоты звука¹).

Эта формула применима постольку, поскольку определяемый ею коэффициент поглощения мал: должно быть мало относи­тельное убывание амплитуды на расстояниях порядка длины волны (т. е. должно быть ус/со >С 1). На этом предположении по существу основан изложенный вывод, так как мы вычисляли диссипацию энергии с помощью незатухающего выражения для звуковой волны. Для газов это условие фактически всегда вы­полнено. Рассмотрим, например, первый член в (79,6). Условие-ус/а> <С 1 означает, что должно быть vco/c² <С l.Ho, как известно из кинетической теории газов, коэффициент вязкости v газа — порядка величины произведения длины свободного пробега / на среднюю тепловую скорость молекул; последняя совпадает по порядку величины со скоростью звука в газе, так что v ~ /с. Поэтому имеем:

так как заведомо / «С к. Член с теплопроводностью в (79,6) дает то же самое, поскольку % ~ v.

') Специфический механизм поглощения должен иметь место при рас­пространении звука в.двухфазной среде — эмульсии (М. А. Исакович, 1948). Ввиду различия в термодинамических свойствах компонент эмульсии измене­ния их температуры при прохождении звуковой волны будут, вообще говоря, различны. Возникающий при этом между ними теплообмен приведет к допол­нительному поглощению звука. Вследствии сравнительной медленности этого теплообмена уже сравнительно рано возникает и существенная дисперси* звука.

Что же касается жидкостей, то и здесь условие малости по­глощения выполняется всегда, когда вообще имеет смысл задача о поглощении звука в той постановке, о которой здесь шла речь. Поглощение (на длине волны) может стать большим, лишь если силы вязких напряжений сравнимы с силами давления, возни­кающими при сжатии вещества. Но в таких условиях становится неприменимым уже самое уравнение Навье — Стокса (с не зави­сящими от частоты коэффициентами вязкости) и возникает су­щественная, связанная с процессами внутреннего трения диспер­сия звука').

При поглощении звука соотношение между волновым векто­ром и частотой можно, очевидно, написать в виде

k=-^ + icm² (79,8)

(где а — коэффициент в (79,6)). Легко сообразить соответствен­но этому, каким образом надо видоизменить уравнение бегущей звуковой волны для того, чтобы учесть в нем эффект поглоще­ния. Для этого замечаем, что в отсутствии поглощения диффе­ренциальное уравнение для, скажем, давления р' = р'(х — ct) Можно написать в виде

dp' _ 1 др'
дх с dt

Уравнение же, решением которого была бы функция е'(**-«<> с k из (79,8), надо, очевидно, написать в виде

~дТ⁼⁼~7~дТ^~ ^a~dF~' (^79,9)

Если ввести вместо t переменную т = t — х/с, то это уравнение перейдет в

dp' ау дх " ат² •

т. е. уравнение типа одномерного уравнения теплопроводности.

Общее решение этого уравнения можно написать в виде (см. §51)

{где р'₀(х) = р' (0, т)). Если волна излучалась в течение огра­ниченного промежутка времени, то на достаточно больших

') Особый случай, когда возможно сильное поглощение звука, которое может быть рассмотрено обычными методами, — газ с аномально большой (по сравнению с его вязкостью) теплопроводностью, связанной с посторон­ним-,! причинами, например, с лучистой теплопроводностью при очень высоких температурах (ср. задачу 3 этого параграфа).

расстояниях от источника это выражение переходит в

р'(х,т) = —j=e-W*\p'_Q(x')dx'. (79,11):

Другими словами, на больших расстояниях профиль волны оп­ределяется гауссовой кривой. Его ширина ~ (ах)^1/2, т. е. растет пропорционально корню из пройденного волной расстояния, амплитуда же волны надает как х~¹¹². Отсюда легко заключить, что полная энергия волны падает по тому же закону х~^1/2. Легко вывести аналогичные формулы для шаровых волн.

При этом надо учитывать, что для такой волны \^p'dt = Q'

(см. (70,8)). Вместо (79,11) получим теперь

р' (Г, т) = Const П5—

^н г дх г¹'²

или

p'(r, т) = const ^ e-*'^iar. (79,12)

Сильное поглощение должно происходить при отражении звуковой волны от твердой стенки. Причина этого явления со­стоит в следующем (К. F. Herzfeld, 1938; Б. П. Константинов,. 1939).

*) Что касается нормальной составляющей скорости, то на стенке она равна нулю уже в силу граничных условий для идеальной жидкости.

В звуковой волне наряду с плотностью и давлением испыты­вает периодические колебания около своего среднего значения также и температура. Поэтому вблизи твердой стенки имеется периодически меняющаяся по величине разность температур между жидкостью и стенкой, даже если средняя температура жидкости равна температуре стенки. Между тем на самой по­верхности температуры соприкасающихся жидкости и стенки должны быть одинаковыми. В результате в тонком пристеноч­ном слое жидкости возникает большой градиент температуры; температура быстро меняется от своего значения в звуковой волне до температуры стенки. Наличие же больших градиентов-температуры приводит к большой диссипации энергии путем теплопроводности. По аналогичной причине к большому погло­щению звука приводит при наклонном падении волны также и вязкость жидкости. При таком падении скорость жидкости в волне (по направлению распространения волны) имеет отличную от нуля компоненту, касательную к поверхности стенки. Между тем на самой поверхности жидкость должна полностью «прили­пать» к стенке. Поэтому в пристеночном слое жидкости возни­кает большой градиент касательной составляющей скорости¹), что и приводит к большой вязкой диссипации энергии (см. за­дачу 1).

Задачи

1. Определить долю энергии, поглощаемой при отражении звуковой вол­ны от твердой стенки. Плотность вещества стенки предполагается настолько большой, что звук практически не проникает в него, а теплоемкость — на­столько большой, что температуру стенки можно считать постоянной.

Решение. Выбираем плоскость стенки в качестве плоскости х = 0, а плоскость падения в качестве плоскости х, у. Угол падения (равный углу •отражения) есть 9. Изменение плотности в падающей волне в некоторой точке на поверхности (скажем, в точке д; = у = 0) есть р[ = Ae~^iat. Отра­женная волна имеет ту же амплитуду, так что у стенки в ней р'₂ = р\. Реаль-• ное изменение плотности жидкости, в которой распространяются одновре­менно обе волны (падающая и отраженная), есть р'=2Лв~'^и>£. Скорость.жидкости в волне определяется согласно

Полная скорость на стенке v = v_t + va есть поэтому

0 = _о =2Л sin 9— в~^ш
UР

(вернее, это есть то значение скорости, которое она имеет без учета верных граничных условий на поверхности стенки при наличии вязкости). Истинный ход скорости v_y вблизи стенки определяется формулой (24,13), а связанная с вязкостью диссипация энергии — формулой (24,14), в которые надо вместо f₀e ^Ulit подставить полученное выше выражение для v.

Отклонение Т температуры от своего среднего значения (равного темпе­ратуре стенки) без учета правильных граничных условий на стенке получилось бы равным (см. (64,13))

с_рр

"В действительности же распределение температуры определяется уравнением ■теплопроводности с граничным условием Т' = 0 при х«9 и соответственно -этому изображается формулой, в точности аналогичной (24,13).

Вычисляя связанную с теплопроводностью диссипацию энергии согласно первому члену формулы (79,1), получим в результате для полной диссипации энергии, отнесенной к единице площади поверхности стенки:

Л²с² У2ю Р

["\/х (-^--l) + sin²9VT].

cpv_l cos 9 = — cos 9.

Средняя плотность потока энергии, падающего на единицу поверхности стенки с падающей волной, равна

2р

.Поэтому доля энергии, поглощающейся при отражении, есть

[sin²9Vv +(^--l)Vx].

§то выражение справедливо лишь до тех пор, пока оно мало (при выводе Цы считали амплитуды падающей и отраженной волн одинаковыми). Это ус-.ловие означает, что угол падения 9 не должен быть слишком близким к я/2.

2. Определить коэффициент поглощения звука, распространяющегося по

цилиндрической трубе.

Решение. Основная доля поглощения обусловлена эффектом, происхо­дящим от наличия стенок. Коэффициент поглощения у равен энергии, дисси-пируемой в единицу времени на поверхности стенок единицы длины трубы, деленной на удвоенный полный поток энергии через поперечное сечение трубы. Вычисление, аналогичное произведенному в задаче 1, приводит к результату (R — радиус трубы):

3. Найти закон дисперсии для звука, распространяющегося в среде с очень большой теплопроводностью.

Решение. При наличии большой теплопроводности движение в звуко­вой волне не адиабатично. Поэтому вместо условия постоянства энтропии имеем теперь уравнение

*' = ^дг (1)

(линеаризованное уравнение (49,4) без вязких членов). В качестве второго уравнения берем

р' = Др', (2)

получающееся путем исключения v из уравнений (64,2—3). Выбирая в каче­стве основных переменных р' и Т', пишем р' и s' в виде

Эти выражения подставляем в (1) и (2), после чего ищем Т, р' в виде, про­порциональном е' ^: <**-<»*). Условие совместимости получающихся таким обра­зом двух уравнений для р' и Т' можно привести (путем использования ряда известных соотношений между производными от термодинамических величин) к виду

к 4 %) %4

чем и определяется искомая зависимость k от со. Здесь введены обозначения

„2

cl-

л ар Л' ^Ст~\до)т~ у

(у — отношение теплоемкостей с_р/с»).

В предельном случае малых частот (со < с²/х) уравнение (3) дает

(4i)'

что соответствует распространению звука с обычной «адиабатической» ско­ростью c_s и малым коэффициентом поглощения, совпадающим со вторым чле­ном в (79,6). Так И должно было быть, поскольку условие о < сЧ% озна­чает, что за вре мя о дного периода тепло успевает распространиться лишь на расстояние ~Vx/<*> (ср. (51,7)), малое по сравнению с длиной волны с/&>.

В обратном предельном случае больших частот из (3) находим:

В этом случае звук распространяется с <изотермической> скоростью с_т '(всегда меньшей скорости c_s). Коэффициент же поглощения оказывается сно­ва малым (по сравнению с обратной длиной волны), причем он не зависит от частоты и обратно пропорционален теплопроводности¹).

4. Определить дополнительное поглощение звука, распространяющегося в смеси двух веществ, связанное с диффузией (И. Г. Шапошников и 3. А Гольдберг, 1952).

Решение. В смеси имеется дополнительный источник поглощения звука, связанный с тем, что возникающие в звуковой волне градиенты температуры и давления приводят к появлению необратимых процессов термо- и бародиф-фузии (градиента же массовой концентрации, а с ней и чистой диффузии, очевидно, не возникает). Это поглощение определяется членом

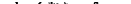в скорости изменения энтропии (59,13) (мы обозначим здесь концентрацию посредством С в отличие от скорости звука с). Диффузионный поток

с k„ из (59,10). Вычисление, аналогичное произведенному в тексте, с исполь­зованием ряда соотношений между производными термодин<"-¹"'егк1тх чин приводит к следующему результату: к выражению (79,6) для фициента поглощения добавляется член

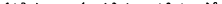Yd

Da²

р. т

5. Определить эффективное сеч ение поглощения звука шариком, радиус которого мал по сравнению с Vv/ш.

в согласии с (52,15). В случае же к>% > с² получается

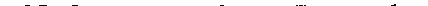
Решение. Полное поглощение складывается из эффектов вязкости и теплопроводности газа. Первый определяется работой стоксовой силы трения при обтекании шарика движущимся в звуковой волне газом (как и в за­даче 3 § 78, предполагается, что шарик не увлекается этой силой). Второй эффект определяется количеством тепла <?, передаваемым в единицу времени от газа шарику (задача 3 § 78): диссипация энергии при передаче тепла q при разности температур V между газом (вдали от шарика) и шариком равна qf'IT. Для суммарного эффективного сечения поглощения получается выражение

_e_i=L[₃v + 2_X(4e.-i)].

§ 80. Акустическое течение

Одно из самых интересных проявлений влияния вязкости на звуковые волны состоит в возникновении стационарных вихре­вых течений в стоячем звуковом поле при наличии твердых пре­пятствий или ограничивающих его твердых стенок. Это движе­ние (его называют акустическим течением) появляется во вто­ром приближении по амплитуде волны; его характерная особен­ность состоит в том, что скорость движения в нем (в простран­стве вне тонкого пристеночного слоя) оказывается не завися­щей от вязкости, — хотя самим своим возникновением оно обя­зано именно вязкости (Rayleigh, 1883).

Свойства акустического течения наиболее типичным образом проявляются в условиях, когда характерная длина задачи (раз­меры препятствий или области движения) малы по сравнению с длиной звуковой волны X, но в то же время велики по сравне­нию с введ енной в § 24 глубиной проникновения вязких волн б = у 2v/co:

Х>/>6. (80,1)

Ввиду последнего условия, в области движения можно выде­лить узкий акустический пограничный слой, в котором происхо­дит падение скорости от ее значения в звуковой волне до нуля на твердой поверхности. Поскольку скорость газа в этом слое (как и в самой звуковой волне) мала по сравнению со скоростью звука, а его характерный размер — толщина б — мал по сравне­нию с а (ср. условие (10,17)), то движение в нем можно рас­сматривать как несжимаемое.

Дата добавления: 2014-11-07