Ol — V2X 53 страница

w + -у == const,

где const — величина, постоянная вдоль каждой из линий тока (если же движение потенциально, то const одинакова и для раз­ных йиний тока, т. е. во всем объеме жидкости). Если на одной линии тока есть точка, в которой скорость газа равна нулю, то можно написать уравнение Бернулли в виде

V²

w-\- у = w₀, (83,1)

где wo — значение тепловой функции в точке с v = 0.

Уравнение сохранения энтропии при стационарном движении сводится к vVs = vds/dl = 0, т. е. s = const, где const есть опять величина, постоянная вдоль линии тока. Напишем это уравнение в виде, аналогичном (83,1):

s = s_a. (83,2)

Из уравнения (83,1) видно, что скорость v больше в тех ме­стах, где тепловая функция до меньше. Максимальное (вдоль данной линии тока) значение скорость имеет в точке, в которой w минимально. Но при постоянной энтропии имеем dw = dp/p; поскольку р > 0, то дифференциалы dw и dp имеют одинако­вые знаки и потому изменение дойр направлено всегда в одну сторону. Следовательно, можно сказать, что вдоль линии тока скорость всегда падает с увеличением давления, и наоборот.

Наименьшее возможное значение давление и тепловая функ­ция получают (при адиабатическом процессе) при равной нулю абсолютной температуре Т = 0. Соответствующее значение дав­ления есть р = 0, а значение до при 7" = 0 примем условно за нулевое значение, от которого отсчитывается энергия; тогда бу­дет и w — 0 при Т = 0. Из (83,1) заключаем теперь, что наи­большее возможное значение скорости (при заданном значении термодинамических величин в точке с v = 0) равно

^тах = (^83,3>

Эта скорость может достигаться при стационарном вытекании газа в вакуум').

Выясним теперь характер изменения вдоль линии тока плот­ности потока жидкости / = pv. Из уравнения Эйлера (vV)v = = —Vp/p находим, что вдоль линии тока имеет место соотноше­ние

vdv + ^- = 0 Р

между дифференциалами dv и dp. Написав dp — c²dp, имеем отсюда

dP Р» _т«

лГ 1^- («3,4)

'(!-■?)• (83,5)

и затем:

rf(po) dv

Отсюда видно, что по мере возрастания скорости вдоль линии тока плотность потока возрастает до тех пор, пока скорость остается дозвуковой. В области же сверхзвукового движения плотность потока падает с увеличением скорости и обращается в нуль вместе с р при v = v_max (рис. 52). Это существенное раз­личие между до- и сверхзвуковыми стационарными потоками может быть истолковано наглядно еще и следующим образом. В дозвуковом потоке линии тока сближаются друг с другом в

') В действительности, конечно, при сильном понижении температуры должна произбйти конденсаций газа и образование двухфазной системы — тумана.

направлении увеличения скорости. При сверхзвуковом же дви­жении линии тока расходятся по мере увеличения скорости.

Поток / имеет максимальное значение /„ в точке, в которой скорость газа равна местному значению скорости звука:

;.=р.с., (83,6)

где буквы с индексом „ показывают значения соответствующих величин в этой точке. Скорость у* = с* называют критической,

1,00 0,75

0,50

0,25

В общем случае произвольного газа критические значения вели­чин могут быть выражены через значения величин в точке с v = 0 в результате совместного решения уравнений

&

s, = s₀, w, + -j- = w₀. (83,7)

Очевидно, что всякий раз, когда число М = v/c < 1, мы бу­дем также, иметь v/c_t < 1, а когда М > 1, то и и/с* > 1. По­этому в данном случае отношение М* = а/с* может служить критерием, аналогичным числу Маха, и даже более удобным, по­скольку с* есть величина постоянная в противоположность ско­рости с, меняющейся вдоль потока.

В применениях общих уравнений гидродинамики особое ме­сто занимает термодинамически идеальный газ. Говоря о таком газе, мы будем всегда (за исключением только особо оговорен­ных случаев) считать, что его теплоемкость является постоянной величиной, не зависящей от температуры (в интересующей нас температурной области). Такой газ часто называют политроп-ным; мы будем пользоваться этим термином, имея в виду под­черкнуть каждый раз, что речь идет о предположении, идущем гораздо дальше термодинамической идеальности. Для политроп-ного газа известны все соотношения между термодинамическими величинами, выражающиеся к то'му же весьма простыми фор­мулами; это часто дает возможность до конца решать уравне­ния гидродинамики. Выпишем здесь, для справок, эти соотноше­ния, которыми нам неоднократно придется пользоваться в даль­нейшем.

Уравнение состояния термодинамически идеального газа гла­сит

_PV = pJp = RW, (83,8)

где R = 8,314-10⁷ эрг/К-моль — газовая постоянная, а р — моле­кулярная масса газа. Скорость звука в таком газе была вычис­лена в § 64 и дается формулой

c² = y№ = yp/_p, (83,9)

где введено отношение теплоемкостей

y = c_p/c_v.

Это отношение всегда больше единицы, а для политропного газа оно постоянно. Для одноатомных газов у = 5/3, а для двух­атомных у = 7/5 (при обычных температурах)¹).

Внутренняя энергия политропного газа с точностью до несу­щественной аддитивной постоянной равна

в = ^=^_т=_7Т^_тг. (83,10)

Для тепловой функции имеют место аналогичные формулы

до = _СрГ = ^-=₇^_т. (83,11)

Здесь учтено известное соотношение с_р — c_v = R/p,. Наконец, энтропия газа

s = c₀ln-^- =c_pln-£—. (83,12)

Вернемся к изучению стационарного движения и применим полученные выше общие соотношения к политропному газу. Под­ставив (83,11) в (83,3), найдем, что максимальная скорость стационарного вытекания равна

Утах = С₀ Д/^Т- (83,13)

Для критической же скорости из второго уравнения (83,7) по­лучим:

*) Название газа «политропный» происходит от термина «политропный процесс» — процесс, в котором давление меняется обратно пропорционально некоторой степени объема Для газа с постоянными теплоемкостями таковым является не только изотермический, но и адиабатический процесс, для кото­рого pV^y= const (адиабата Пуассона). Отношение теплоемкостей у назы­вают показателем адиабаты.

^ + "2- = ^ = —Г,

откуда >')

с. = с₀ д/тТТ- ^(83,14)

Уравнение Бернулли (83,1) после подстановки выражения (83,11) для тепловой функции даст соотношение между темпе­ратурой и скоростью в произвольной точке линии тока; анало­гичные соотношения для давления и плотности можно затем написать с помощью уравнения адиабаты Пуассона:

Таким образом, получим следующие важные формулы:

-Ч'-^^-Ч'-^)*- ⁽⁸³'^,6) '-Ч'-^^-Ч'-^?)*-

Иногда удобно пользоваться этими соотношениями в виде, опре­деляющем скорость через другие величины:

»^!=^rt[> -(irl-M¹ - (*)"']■ ™™

Выпишем также соотношение, связывающее скорость звука со скоростью и:

c^cl-r^l_v^l+l_c^l=l_v2. _(83>! ₈₎

Отсюда найдем, что числа М и М, связаны друг с другом по­средством

M.^j= _2т1^у¹-1 • <⁸³'¹⁹>

Когда М растет от 0 до оо, М² растет от 0 до (у -f- 1)/(у— 1).

') На рис. 52 дан график отношения ///* в функции от к/с* для воздуха Ь = 1,4, и_ша* = 2,45с»).

Наконец, приведем выражения для критических значений температуры, давления и плотности; они получаются при v = с„ из формул (83,16)'):

V1

т.=ТТТ. р.^Ро^Г'.р. = р.(т|т)^т"¹- ⁽⁸³'²⁰⁾

Подчеркнем в заключение, что полученные здесь результаты относятся к движению, при котором не возникают ударные вол­ны. При наличии ударных волн не имеет места уравнение (83,2): при прохождении линии тока через ударную волну энтро­пия газа возрастает.

Мы увидим, однако, что уравнение Бернулли (83,1) остается справедливым и при наличии ударной волны, так как до -+- v²/2 является как раз одной из величин, сохраняющихся при про­хождении через поверхность разрыва (§ 85); вместе с ним остается, например, справедливой и формула (83,14).

Задача

Выразить температуру, давление и плотность вдоль линии тока через число М = vie.

Решение. С помощью полученных в тексте формул получим

§ 84. Поверхности разрыва

В предыдущих главах мы рассматривали только такие тече­ния, при которых распределение всех величин (скорости, давле­ния, плотности и т. д.) в газе непрерывно. Возможны, однако, и движения, при которых возникают разрывы непрерывности в распределении этих величин.

Разрыв непрерывности в движении газа имеет место вдоль некоторых поверхностей; при прохождении через такую поверх­ность указанные величины испытывают скачок. Эти поверхности называют поверхностями разрыва. При нестационарном движе­нии газа поверхности разрыва не остаются, вообще говоря, не­подвижными; необходимо при этом подчеркнуть, что скорость движения поверхности разрыва не имеет ничего общего со ско­ростью движения самого газа. Частицы газа при своем движе­нии могут проходить через эту поверхность, пересекая ее.

') Так, для воздуха (у = 1,4) с* = 0,913 Со, р* = 0,528 ро, р«= 0,634 р₀, Г* = 0,833 Го.

На поверхностях разрыва должны выполняться определен­ные граничные условия. Для формулирования этих условий рас-

смотрим какой-нибудь элемент поверхности разрыва и восполь­зуемся связанной с этим элементом системой координат с осью х, направленной по нормали к нему¹).

Во-первых, на поверхности разрыва должен быть непрерывен поток вещества: количество газа, входящего с одной стороны, должно быть равно количеству газа, выходящему с другой сто­роны поверхности. Поток газа через рассматриваемый элемент поверхности (отнесенный на единицу площади) равен pv_x. По­этому должно выполняться условие p\V\_x = Piv_2x, где индексы 1 и 2 относятся к двум сторонам поверхности разрыва.

Разность значений какой-либо величины с обеих сторон по­верхности разрыва мы будем ниже обозначать посредством квадратных скобок; так,

[Р»*1 = Pl»l* — р2«2х>

и полученное условие напишется в виде

[р»,]=0. (84,1)

Далее, должен быть непрерывным поток энергии. Поток энер­гии определяется выражением (6,3). Поэтому мы получаёк условие

[pv_x (-у + а»)] = 0. (84,2)

Наконец, должен быть непрерывен поток импульса, т. е. должны быть равны силы, с которыми действуют друг на друга газы по обеим сторонам поверхности разрыва. Поток импульса через единицу площади равен (см. § 7)

рп_{ + 9ViV_kn_h.

Вектор нормали п направлен по оси х. Поэтому непрерывность Л'-компоненты потока импульса приводит к условию

[P + Po|] = 0, _{84i3)

а непрерывность у- и z-компонент дает

[pv_xv_y] = 0, [pv_xv_z]=0. ' (84,4)

Уравнения (84,1—4) представляют собой, полную систему гра­ничных условий на поверхности разрыва. Из них можно сразу сделать вывод о возможности существования двух типов поверх­ностей разрыва.

В первом случае через поверхность разрыва нет потока ве­щества. Это значит, что p\v_lx = p₂v_2x = 0. Поскольку pi и р₂

') Если движение нестационарно, то мы рассматриваем элемент поверх­ности в течение малого интервала времени.

ОТЛИЧНЫ ОТ Нуля, ТО ЭТО ЗНачИТ, ЧТО ДОЛЖНО бЫТЬ V\x ■= v_2x == 0.

Условия (84,2) и (84,4) в этом случае удовлетворяются автома­тически, а условие (84,3) дает р\ — р₂. Таким образом, на по­верхности разрыва в этом случае непрерывны нормальная ком­понента скорости и давление газа:

v_lx = v_2x = 0, [р] = 0. (84,5)

Тангенциальные же скорости v_y, v_z и плотность (а также дру­гие термодинамические величины, кроме давления) могут испы­тывать произвольный скачок. Такие разрывы будем называть тангенциальными.

Во втором случае поток вещества, а с ним и v\_x и v_2x отличны от нуля. Тогда из (84,1) и (84,4) имеем:

[v_y] = 0, [о,] = 0, (84,6)

т, е. тангенциальная скорость непрерывна на поверхности раз­рыва. Плотность же, давление (а потому и другие термодина­мические величины) и нормальная скорость испытывают скачок, причем скачки этих величин связаны соотношениями (84,1—3). В условии (84,2) мы можем в силу (84,1) сократить pv_x, а вместо v² можно в силу непрерывности v_y и v_z писать v\. Таким

образом, на поверхности разрыва в рассматриваемом случае должны иметь место условия:

[poj = 0, [^ _{+ ш}] = о, [p + pvl] = 0. (84,7)

Разрывы этого типа называют ударными волнами.

Если теперь вернуться к неподвижной системе координат, то вместо v_x надо везде писать разность между нормальной к по­верхности разрыва компонентой v_n скорости газа и скоростью и самой поверхности, направленной, по определению, по нормали к ней:

v _х = v_n — и. (84,8)

Скорости о_ли«берутся относительно неподвижной системы от­счета. Скорость v_x есть скорость движения газа относительно поверхности разрыва; иначе можно сказать, что —v_x = и—v_n есть скорость распространения самой поверхности разрыва отно­сительно газа. Обращаем внимание на то, что эта скорость раз­лична по отношению к газу с обеих сторон поверхности (если v_x испытывает разрыв).

Тангенциальные разрывы, на которых испытывают скачок ка­сательные компоненты скорости, рассматривались нами уже в § 29. Там было показано, что в несжимаемой жидкости такие разрывы неустойчивы и должны размываться в турбулентную область. Аналогичное исследование для сжимаемой жидкости показывает, что такая неустойчивость имеет место и в общем случае произвольных скоростей (см. задачу 1).

Частным случаем тангенциальных разрывов являются раз­рывы, в которых скорость непрерывна и испытывает скачок только плотность (а с ней и другие термодинамические вели­чины за исключением давления); такие разрывы называют кон­тактными. Сказанное выше о неустойчивости, к ним не отно­сится.

Задачи

1. Исследовать устойчивость (по отношению к бесконечно малым возму­щениям) тангенциальных разрывов в однородной сжимаемой среде (газ или жидкость).

Решение. Вычисления аналогичны произведенным в § 29 для несжи­маемой жидкости. Как и там, по нормали к поверхности направим ось г.

В среде 2 (со скоростью v2 = 0, г < 0) давление удовлетворяет уравне­нию

р₂ — с Арг ⁼ 0

(вместо уравнения Лапласа (29,2) в несжимаемой жидкости). Ищем р'_г в виде

р₂ = const • ехр (— Ш + iqx + Ы_гг),

еде волновое число «ряби» на поверхности обозначено через q (вместо k в § 29); если х₂ комплексно, то оно должно быть выбрано так, чтобы было Im Кг < 0. Волновое уравнение приводит к соотношению

(0² = _c²((/² + x^). (1)

Вместо (29,7) тем же образом находим теперь

p2 = Spco²//w₂.

В газе /, движущемся со скоростью Vi = v (г > 0), ищем р[ в виде р[ = const ■ ехр (— Ш + iqx — ix,z).

Для упрощения выводов предположим сначала, что скорость v направлена тоже по оси х. Соотношение между со, q, щ дается формулой

(со-^)²=_С²(<₇² + к²) (2)

(ср. (68,1)). Вместо (29,6) получаем теперь

р\= — 5 (и — qofp/ixi,

и условие р₁ = р2 приводит к уравнению

*■ +-*|._Д0. (3)

(со — qv)² со²

От сделанного выше предположения о направлении скорости v можно изба­виться, заметив, что невозмущенная скорость входит в исходные линеаризо­ванные уравнение непрерывности и уравнение Эйлера только в комбинации (vV) (соответственно в членах (vV)p' и (vV)v'). Поэтому для перехода к произвольному направлению v (в плоскости ху) достаточно заменить в (1) — (3) v на ucoscp, где ср — угол между v и q (ср. примечание на с. 155).

Исключив Хи %г из (1)—(3), получим следующее дисперсионное уравне­ние для определения частоты возмущения со по волновому числу q:

U____________!______ "1LJ_______!___________!_______ 1 ₌₀ (4)

Leo² (со — qv cos <p)² J L c²q² со² (ш — qv cos <p)² J Корень первого множителя

со = -у- qv cos ср (5)

со = -А- 1

всегда веществен. Корни второго множителя:

[

1 "1^1/3

v² cos² ф + с² ± с (с² + v² cos² ф)¹'²; (6)

эти корни вещественны только при v cos ф > v_k, где

_Dft = 2³% (7)

Таким образом, при v cos ф < v_k дисперсионное уравнение имеет пару комплексно-сопряженных корней, для одного из которых будет Im со > 0; соответствующие возмущения приводят к неустойчивости. При v < v_k таковы возмущения с любым углом ф, а при v > v_k неустойчивы только возмущения С cos ф < v_k/v. В результате тангенциальный разрыв неустойчив всегда. От­метим, что сам факт неустойчивости (если не интересоваться по отношению к каким именно возмущениям) очевиден уже из неустойчивости в случае несжимаемой жидкости в совокупности с тем обстоятельством, что в диспер­сионное уравнение скорость v входит только в комбинации усозф: какова бы ни была скорость v, найдутся такие углы ф, для которых v cos ф < с, так что по отношению к таким возмущениям среда ведет себя как несжимаемая ').

2. На тангенциальный разрыв в однородной сжимаемой среде падает плоская звуковая волна; определить интенсивности отраженной от разрыва волны и волны, преломленной на нем (/. W. Miles, 1957; Н. S. Ribner, 1957).

Решение. Выбираем оси координат, как в предыдущей задаче, причем скорость v (в среде /, z > 0) направлена по оси х. Пусть звуковая волна падает из неподвижной среды (среда 2, г < 0); направление ее волнового вектора к задается сферическими углами 0 и ф; угол 0 — между к и осью г, угол ф — между проекцией к на плоскость ху (обозначим ее q) и скоростью vr

k_x=*q cos ф, k_yt=q sin ф, k_x = -у- sin 0, q = sin 0 = k sin 0,

причем 0 < 0 < я/2 (волна падает в положительном направлении оси z), В среде 2 ищем давление в виде

где A — амплитуда отраженной волны, а амплитуда падающей волны условно принята за единицу. В среде 1 имеем одну преломленную волну:

Pi

⁴) Значение (7) получено Л. Д. Ландау (1944). Необходимость учета в этой задаче неколлинеарности v и q указана С. Я. Сыроватским (1954).

где ч удовлетворяет уравнению

1-4- Л = В, _т___гв--4-(1_Л),

(ср. (2)). Амплитуды А и В определяются из условий непрерывности дав­ления и вертикального смещения жидких частиц по обе стороны разрыва: р, = р₂ при z=0, £i = £2=£- Это дает два уравнения

________ *«

(со — oft*)² откуда

_ (to — vkxYJK — a>²/k_{2 =} 2 (ш — vk_x)²/K

(u>-vk_x)²!>i + <i>²/k₂ ' (св - Ыг*)²/х + <o²/fe_z '^{а>

чем и решается поставленная задача. Знак величины х,

•л² — -^з- [(1 —• М sin 9 cos ф)² — sin² В], М = —,
с² с

должен быть выбран с учетом предельных условий при z->-oo: скорость пре­ломленной волны должна быть направлена от разрыва, т. е.

С7_г = ^- = _^1_>0. (9)

ох ю — vk_x

Из полученных формул видно, что возможны три различных режима от­ражения.

1) При М cos ф ■< 1/sin 9—1 величина х вещественна, а поскольку со — vk_x > 0, то согласно условию (9) х > 0. Из (8) видно, что при этом \А\ •< 1 — отражение происходит с ослаблением волны.

2) При 1/sin 9—1 < М cos ф < 1/sin 9 + 1 величина х мнима и |А|=< = 1, — происходит полное внутреннее отражение звуковой волны.

3) При М cos ф > 1 -f 1/sin 0 (что возможно лишь при М > 2) величи­на х снова вещественна, но теперь надо выбрать х < 0. Согласно (8) при этом |Л| > 1, т.е. отражение происходит с усилением волны. Более того, знаменатели выражений (8) с х < 0 могут обратиться в нуль при определен­ных углах падения волны, и тогда коэффициент отражения обращается в бес­конечность. Поскольку этот знаменатель совпадает (с точностью до обозна­чений) с левой стороной уравнения (3) предыдущей задачи, то можно сразу заключить, что «резонансные» углы падения определяются равенствами (5) и (6) (последнее — при М > 2^3/2). В свою очередь, бесконечность коэффи­циента отражения (и прохождения), т.е. конечность амплитуды отраженной волны при стремящейся к нулю амплитуде падающей волны, означает воз­можность спонтанного излучения звука поверхностью разрыва: раз созданное на ней возмущение (рябь) неограниченно долго продолжает излучать звуко­вые волны, не затухая и не усиливаясь при этом; энергия, уносимая излучае­мым звуком, черпается из всей движущейся среды.

Плотность потока энергии (усредненная по времени) в преломленной волне

а Ц Ё - ^{сЧЮ 1В |2}

^{2 2} to — vk_x (о — vk_x 2рс²

{Ei из (68,3)). В случае 3 имеем х < 0, а потому и 172 < 0, — энергия при­ходит к разрыву из движущейся среды, что и служит источником усиления. При спонтанном излучении звука эта приходящая энергия совпадает с энер­гией, уносимой волной, уходящей в неподвижную среду.

В изложенном решении задачи неустойчивость поверхности разрыва не учитывается. Формальная корректность такой постановки задачи связана с тем, что звуковые волны и неустойчивые поверхностные (затухающие при z-»-±oo) еолны представляют собой линейно независимые колебательные моды. Физическая же корректность требует соблюдения специальных условий (например, начальных), в которых поверхностные волны еще достаточно слабы.

§ 85. Ударная адиабата

Перейдем к подробному изучению ударных волн¹). Мы ви­дели, что в этих разрывах тангенциальная компонента скорости газа непрерывна. Можно поэтому выбрать систему координат, в которой рассматриваемый элемент поверхности разрыва по­коится, а тангенциальная компонента скорости газа по обе сто­роны поверхности равна нулю²). Тогда можно писать вместо нормальной компоненты v_x просто v и условия (84,7) напишутся в виде

Р101 = Р₂»2 = /. (85,1)

P₁ + P₁f² = P₂ + p2^y2> (85,2)

2 2

ш_! + -^- = ш₂ + -у-, (85,3)

где / обозначает плотность потока газа через поверхность раз­рыва. Мы условимся в дальнейшем всегда считать j положитель­ным, причем газ переходит со стороны / на сторону 2. Другими словами, мы будем называть газом / тот, в сторону которого движется ударная волна, а газом 2 — газ, остающийся за ней. Сторону ударной волны, обращенную к газу /, будем называть передней, а обращенную к газу 2 — задней.

Выведем ряд соотношений, являющихся следствием написан­ных условий. Введем удельные объемы V\ = 1/pi, V₂—1/рг газа. Из (85,1) имеем:

у_{1 = /}у„ v₂ = jV₂ (85,4)

и, подставляя в (85,2):

P. + /V, = p₂ + i²V₂, (85,5)

или

f = "^7- (85,6)

') Сделаем одно терминологическое замечание. Под ударной волной мы понимаем самую поверхность разрыва. В литературе, однако, можно встре­тить и другую терминологию, в которой поверхность разрыва называют фрон­том ударной волны, а под ударной волной понимают поверхность разрыва вместе со следующим за ним течением газа. ²) Такой выбор системы координат будет подразумеваться везде в этой главе, за исключением § 92. Неподвижную ударную волну часто называют скачком уплотнения. Если неподвижная ударная волна перпендикулярна к направлению потока, то юворят о прямом скачке уплотнения; если же она наклонна к направлению движения, то говорят о косом скачке уплотнения.

Эта формула (вместе с (85,4)) связывает скорость распростра­нения ударной волны с давлениями и плотностями газа по обеим сторонам поверхности.

Поскольку /² — величина положительная, то должно быть одновременно р₂ > рь Vi > V₂ или р₂ < р_и Vi < V₂; мы уви­дим в дальнейшем, что в действительности возможен лишь пер­вый случай.

Отметим еще следующую полезную формулу для разности
скоростей v\ — v₂. Подставляя (85,6) в v\— v₂ = j(V\—V₂), по-
лучаем¹):

Oi-o₂ = V(P2-P₁)(^-^2). (85,7)

Далее, пишем (85,3) в виде

w₁+-_T^L = w₂ + -^- (85,8)

и, подставляя /² из (85,6), получаем:

t»i - Щ + j (Vi + V₂) (р₂ - _Pl) = 0. (85,9)

Если ввести вместо тепловой функции внутреннюю энергию е согласно е = w — pV, то полученное соотношение можно напи­сать в виде

ei - е₂ + (Vi - V₂) (_Pl + р₂) = 0. (85,10)

Эти соотношения определяют связь между термодинамическими величинами по обе стороны поверхности разрыва.

') Мы пишем здесь квадратный корень с положительным знаком, заранее имея в виду, что должно быть Vi — v₂ > 0, как это будет выяснено ниже (§ 87).

При заданных р_ь V\ уравнение (85,9) или (85,10) опреде­ляет зависимость между р₂ и V₂. Об этой зависимости говорят как об ударной адиабате или адиабате Гюгонио (W. J. Rankine, 1870; Н. Hugoniot, 1885). Графически она изображается (рис.53) в плоскости р, V кривой, проходящей через заданную точку р_и Vi, отвечающую состоянию газа 1 перед ударной волной; эту точку ударной адиабаты мы будем называть ее начальной точ­кой. Отметим, что ударная адиабата не может пересечь верти­кальной прямой V =V\ нигде, кроме только начальной точки. Действительно, наличие такого пересечения означало бы, что одному и тому же объему соответствуют два различных давле­ния, удовлетворяющих уравнению (85,10). Между тем, при Vi = V₂ имеем из (85,10) также и ei=e₂, а при одинаковых объемах и энергиях давления тоже должны быть одинаковыми. Таким образом, прямая V = Vi делит ударную адиабату на две части, из которых каждая находится целиком по одну сторону от этой прямой. По аналогичной причине ударная адиабата пе­ресекает только в одной точке (pi, Vi) также и горизонтальную прямую р = pi.

Пусть аа' (рис. 54) есть ударная адиабата, проведенная че­рез точку рь V] в качестве начальной. Выберем на ней какую-нибудь точку р₂, V₂ и проведем через нее другую адиабату (bb')_t для которой бы эта точка была начальной. Очевидно, что пара значений р_ь V\ будет удовлетворять также и уравнению этой второй адиабаты. Таким образом, адиабаты аа' и bb' пересе­кутся в обеих точках pi, V\ и рг, V₂. Подчеркнем, что обе эти адиабаты отнюдь не совпадают полностью друг с другом, как это имело бы место для адиабат Пуассона, проведенных через заданную точку.

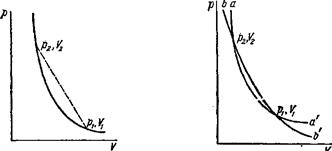
Рис. 53 Рис. 54

Это обстоятельство является одним из следствий того факта, что уравнение ударной адиабаты не может быть написано в виде Др, V) = const, где / есть некоторая функция своих аргументов, как это, например, имеет место для адиабаты Пуассона (урав­нение которой есть s(p, V) = const). В то время как адиабаты Пуассона (для заданного газа) составляют однопараметрическое семейство кривых, ударная адиабата определяется заданием двух параметров: начальных значений р\, V\. С этим же свя­зано и следующее важное обстоятельство: если две (или более) последовательные ударные волны переводят газ соответственно из состояния / в состояние 2 и из 2 в 3, то переход из состоя­ния / в 3 путем прохождения какой-либо одной ударной волны, вообще говоря, невозможен.

Дата добавления: 2014-11-07