Ol — V2X 52 страница

Рассмотрим акустический пограничный слой у плоской твер­дой стенки (плоскость xz), причем движение будем считать пло­ским — в плоскости ху (Н. Schlichting, 1932). Приближения, связанные с малой толщиной пограничного слоя, описаны в § 39 и сохраняют силу для рассматриваемого нестационарного дви­жения. Нестационарность приводит лишь к появлению в урав­нении Прандтля (39,5) членов с производными по времени:

(производная dp/dx выражена через скорость U(x,t) течения вне пограничного слоя с помощью уравнения (9,3)). В данном случае

U = v_Q cos kx • cos at = v_Q cos kx • Re е~^ш (80,3)

(/г = ю/с), что соответствует стоячей плоской звуковой волне с частотой со. Искомую скорость v в пограничном слое выразим через функцию тока ф(л;, у, t) согласно

dip дф

^Vx~~dy' ^Vy~ дх~'

чем автоматически удовлетворяется уравнение непрерывности (39,6).

Будем решать уравнение (80,2) последовательными прибли­жениями по малой величине vo — амплитуде колебаний скорости газа в звуковой волне. В первом приближении пренебрегаем квадратичными членами полностью. Решение уравнения

удовлетворяющее требуемым условиям при у = 0 и у = со, есть ₀<1) ₌ R_e |_{0q cos} ^. _е-ш (\ _ e-*v)},

где

Соответствующая функция тока (удовлетворяющая условию фО> = 0 при у — 0, эквивалентному условию ^о(„^{1) =} 0) есть

^) = ile{v_Qcoskx • g^l)(y)e-^lb,t}, (80,5)

В следующем приближении пишем v = v⁽¹⁾ + v⁽²> и для ско­рости v^(2> получаем из (80,2) уравнение

3t><²> d²vf dU to™ dv«>

~ЬЧ ^v ~bY~ ^{= U} ~~E7 ~ ^v* ~ЬЧ -af ■ ⁽⁸°'⁶⁾

В правой стороне имеются члены с частотами © + (0 = 2(0 и © — ю = 0. Последние приводят к появлению в v⁽²⁾ не завися­щих от времени членов, которые и описывают интересующее нас стационарное движение; ниже мы будем понимать под v⁽²⁾ только эту часть скорости. Соответствующую часть функции тока пишем в виде

^=—sm2kx-^{y) (80,7)

и для функции £⁽²⁾(#) находим уравнение

6²ф<²>'" = 1 - 11 f + 1 Re (&r £<>>"), (80,8)

где штрихи рзначают дифференцирование по у.

Решение этого уравнения должно удовлетворять условиям £^<2)(0) = 0, £^(2)/(0) = 0> эквивалентным требованию v^{2) = v^{2) — О на твердой поверхности. Что же касается условий вдали от стен­ки, то можно лишь потребовать, чтобы скорость v^{2) стремилась к конечному значению (но не к нулю). Подстановка (80,5) в (80,8) и двукратное интегрирование приводят к следующему ре­зультату для производной £^(2)/:

£<²>' (у) = 1 _ 1 е~²У'^й - e-yi⁶ sin -| - -\ е-ш* cos -| +

+ 4^^/e(cos|-sin|).

При у-*~оо она стремится к значению

£<2>'(со) = 3/8, (80,9)

чему отвечает скорость

За²,

о«(оо) = sin 2kx. (80,10)

Этот результат демонстрирует указанное в начале параграфа явление. Мы видим, что вне пограничного слоя возникает (во втором приближении по vo) стационарное движение, скорость ко­торого не зависит от вязкости. Ее значение (80,10) служит гра­ничным условием при определении акустического течения в ос­новной области движения (см. задачу)¹).

Задача

Определить акустическое течение в пространстве между двумя плоско­параллельными стенками (плоскости у = 0 и y = h), в котором имеется стоячая звуковая волна (80,3). Расстояние h между плоскостями (играющее роль характерной длины /) удовлетворяет условиям (80,1) (Rayleigh, 1883).

') Поперечная скорость, отвечающая продольной скорости (80,9), есть ^vf =------ ~-ycos2kx<_VM При решении задачи о движении вне пограничного слоя эта скорость воз­никает автоматически в силу уравнения непрерывности, если поставить гра­ничное условие о^' = 0 при у = 0. ²) Другими словами, отношение v₀/c предполагается малым по сравнению со всеми другими малыми параметрами задачи; в частности, v₀U<g_6lh.

Решение. Ввиду малости скорости и⁽²> искомого стационарного дви­жения по сравнению со скоростью звука, его можно считать несжимаемым. ■Более того, ввиду предполагаемой сколь угодной малости скорости Vo в зву-ковой волне (а вместе с ней и скорости v^y ~ ^vo/c)< ^в уравнении движения можно пренебречь квадратичными членами²). Тогда уравнение (15,12) для

функции тока сводится к уравнению

⁴V»-(£+&)>-

'(отметим, что оно возникает из члена с вязкостью, но сама вязкость из него выпадает). Ищем ф^<2) в виде (80,7). Ввиду условия Л < А производные по у велики по сравнению с производными по х; пренебрегая последними, получим для функции £⁽²⁾(#) уравнение

£<²>""=0. (1)

Ввиду очевидной симметрии задачи, течение симметрично относительно плоскости (/•= Л/2. Это значит, что

(*, у) = vf (х, Л - у), vf (х, у) = - vf (х, Л - у),

для чего должно быть

£⁽²⁾ (у) = - £^(2> (А - у)-

Таким решением уравнения (1) является

--*-) +'('ЧУ-

Постоянные А и В определяются граничными условиями

£^<2) (0) = 0, f-^y (0) = 3/8. В результате находим для функции тока выражение

Ч> ' =------- s n 26* — [у-------- Н-------------- s---,

16с L V 2 J (Л/2)² Г

а из него следующие окончательные формулы для распределения скоростей1

(2) ^3ао _пь Г, 3(г/-Л/2)²]

о*' = sin 2kx 1 5,

* 16с L (Л/2)² J

Зо²й Г/ Л\ (у - А/2)³ 1

о,7 = ^cos 2kx i i у i s— i.

" 8c IV 2) (h/2)² J

Скорость v*® меняет знак на расстоянии (Л/2) (l — 3^-1/2) = 0,423Л/2 от стенки.

Описываемое этими формулами течение состоит из двух рядов вихрей, симметрично расположенных относительно серединной плоскости у = Л/2 и периодичных вдоль осп х с периодом Х/2.

§ 81. Вторая вязкость

Второй коэффициент вязкости £ (мы будем говорить о нем просто как о второй вязкости) имеет обычно тот же порядок ве­личины, что и коэффициент вязкости ц. Существуют, однако, случаи, когда £ может достигать значений, значительно превы­шающих значения п. Как мы знаем, вторая вязкость проявляет­ся в тех процессах, которые сопровождаются изменением объ­ема (т. е. плотности) жидкости. При сжатии или расширении, как и при всяком другом быстром изменении состояния, в жид­кости нарушается термодинамическое равновесие, в связи с чем в ней начинаются внутренние процессы, стремящиеся восстано­вить это равновесие. Обычно эти процессы настолько быстры (т. е. их время релаксации настолько мало), что восстановле­ние равновесия успевает практически полностью следовать захо­дом изменения объема, если только, конечно, скорость этого изменения не слишком велика.

Существуют случаи, когда время релаксации процессов уста­новления равновесия в теле велико, т. е. эти процессы проте­кают сравнительно медленно. Так, если мы имеем дело с жид­костью или газом, представляющими собой смесь веществ, ме­жду которыми может происходить химическая реакция, то при каждых данных плотности и температуре существует определен­ное состояние химического равновесия, характеризующееся опре­деленными концентрациями веществ в смеси. Если, например, сжать жидкость, то состояние равновесия нарушится и начнет происходить реакция, в результате которой концентрации ве­ществ будут стремиться принять равновесные значения, соответ­ствующие новому значению плотности (и температуры). Если скорость этой реакции не слишком велика, то установление рав­новесия происходит сравнительно медленно и не будет поспевать за изменением сжатия. Процесс сжатия будет сопровождаться тогда внутренними процессами приближения к состоянию равно­весия. Но процессы установления равновесия являются процес­сами необратимыми; они сопровождаются возрастанием энтро­пии и, следовательно, диссипацией энергии. Поэтому, если время релаксации этих процессов велико, то при сжатии или расши­рении жидкости происходит значительная диссипация энергии, и поскольку эта диссипация должна определяться второй вязко­стью, то мы приходим к выводу, что £ будет велико¹).

Интенсивность процессов диссипации, а с ними и величина £, зависит, естественно, от соотношения между скоростью процес­сов сжатия и расширения и временем релаксации. Если, напри­мер, речь идет о сжатиях и расширениях, вызываемых звуковой волной, то вторая вязкость будет зависеть от частоты волны. Та­ким образом, значение второй вязкости не будет просто кон­стантой, характеризующей данное вещество, а само будет за­висеть от частоты того движения, в котором она проявляется. О зависимости величины £ от частоты говорят как о ее дис­персии.

*) Медленным процессом, приводящим к большим £, часто является так­же передача энергии от поступательных степеней свободы молекул к коле­бательным (внутримолекулярным) степеням свободы.

Излагаемый ниже метод общего рассмотрения всех этих яв­лений принадлежит Л. И. Мандельштаму и М. А. Леонтовичу (1937).

Пусть £— некоторая физическая величина, характеризующая состояние тела, а £₀ — ее значение в состоянии равновесия; £<> является функцией от плотности и температуры. Так, для жид­ких (или газовых) смесей величиной | может являться концен­трация одного из веществ в смеси, а £₀ есть тогда значение кон­центрации при химическом равновесии.

Если тело не находится в состоянии равновесия, то величина g будет меняться со временем, стремясь принять значение go-В состояниях, близких к равновесному, разность | — g₀ мала, и можно разложить скорость | изменения | в ряд по этой раз­ности. Член нулевого порядка в этом разложении отсутствует, так как | должно обратиться в нуль в состоянии равновесия, т.е. при | = go. Поэтому с точностью до членов первого порядка имеем:

i=-|(i-y. (8i,i).

Коэффициент пропорциональности между g и g— g₀ должен быть отрицательным, так как в противном случае g не стремилось бы к конечному пределу. Положительная постоянная т имеет размерность времени и может рассматриваться как время релак­сации для данного процесса; чем т больше, тем медленнее про­исходит приближение к равновесию.

В дальнейшем мы будем рассматривать процессы, в которых жидкость подвергается периодическому адиабатическому ') сжа­тию и расширению, так что переменная часть плотности (и дру­гих термодинамических величин) зависит от времени посред­ством множителя е~^ш; речь идет о звуковой волне в жидкости. Вместе с плотностью и другими величинами меняется также и положение равновесия, так что g₀ можно написать в виде £₀ = 1₀₀-г-|₀, где g₀₀ — постоянное значение g₀, соответствующее среднему значению плотности, а |д— периодическая часть, про­порциональная е~^ш. Написав истинное значение g в виде g = = 1оо + £', мы заключаем из уравнения (81,1), что g' тоже яв­ляется периодической функцией времени и связано с 1'₀ посред­ством

6' = Т^5Г- <⁸¹'²>

') Изменение энтропии (в состояниях, близких к равновесному) является величиной второго порядка малости. Поэтому с точностью до величин первого порядка можно говорить об адиабатичности процесса.

Вычислим производную от давления по плотности при рас­сматриваемом процессе. Давление должно теперь рассматри­ваться как функция от значений плотности и величины g в дан­ном состоянии, а также от энтропии, которая предполагается

постоянной и которую мы будем для краткости просто опускать. Имеем:

dp v <Эр Л v ^д1 h ^д? '

Согласно (81,2) подставляем сюда

dl _ dl' _ 1 dl'₀ ^ 1 dt₀ dp «Эр 1 — тх dp 1 — iax dp

и получаем:

dp 1 — кот iv <Эр)\ \ dl J_p dp \ dp)\)

Сумма

\dp)i~^r\db)_Q dp

есть не что иное, как производная от р по р при процессе на­столько медленном, что жидкость находится все время в состоя­нии равновесия; обозначая ее посредством (др/др)_рав„, имеем окончательно:

f=T3W[(f)_pm-^(f)_t]- («Я

Пусть, далее, ро — давление в состоянии термодинамического равновесия; р_й связано с другими термодинамическими величи­нами уравнением состояния жидкости и является при заданных плотности и энтропии вполне определенной величиной. Давление же р в неравновесном состоянии отлично от р₀ и является функ­цией также и от |. Если плотность получает адиабатическое при­ращение бр, то равновесное давление меняется на

^б^=Шрав„^бР'

между тем как полное приращение давления есть (др/др)8р, где др/др определяется формулой (81,3). Поэтому разность р — р₀ между истинным и равновесным давлениями в состоянии с плот­ностью р + бр равна

l dp К dp)равн j 1 — /ют 1Л <ЭР /равн v «Эр /|] ^v

Нас интересуют здесь те изменения плотности, которые обу­словлены движением жидкости. Тогда бр связано со скоростью уравнением непрерывности, которое мы напишем в виде

if + pdivv = 0, где d/dt обозначает полную производную по времени. При пе­риодическом движении имеем: dbp/dt = —£шбр, и поэтому

6р = — div v. Подставляя это выражение в р— р₀, получаем:

Р ~ Ро = Т^Ш- (^со - ^с~) ^й™ ^v> (⁸М>

где введены обозначения

смысл которых выяснится ниже.

Для того чтобы связать полученные выражения с вязкостью жидкости, напишем тензор напряжений о,&. В этот тензор давле­ние входит в виде члена — р&щ. Выделяя отсюда давление ро, определяющееся уравнением состояния, находим, что в неравно­весном состоянии в oik входит дополнительный член

- (Р ~ Ро) 0„ = ! 1⁹_iwr {Cl - Cl) 6_i& diV V.

С другой стороны, сравнивая это с общим выражением (15,2—3) для тензора напряжений, в которое divv входит в виде £divv, мы приходим к результату, что наличие медленных процессов установления равновесия макроскопически эквивалентно нали­чию второй вязкости, равной

£ = T^WK>-^co)- (81.6)

На обычную же вязкость ц эти процессы не влияют. При про­цессах, настолько медленных, что те> <С 1, £ равно

Ео = тР (81,7)

Е; растет с увеличением времени релаксации т в согласии со ска­занным выше. При больших частотах £ оказывается функцией частоты, т. е. обнаруживает дисперсию.

Рассмотрим теперь вопрос о том, каким образом влияет на­личие процессов с большим временем релаксации (для опреде­ленности будем говорить о химических реакциях) на распро­странение звука в жидкости. Для этого можно было бы исхо­дить из уравнения движения вязкой жидкости с %, определяе­мым формулой (81,6). Проще, однако, рассматривать движение формально как не вязкое, но с давлением р, определяющимся не уравнением состояния, а полученными здесь формулами. Тогда все известные нам уже из § 64 общие соотношения остают­ся формально применимыми. В частности, связь волнового век-

тора с частотой по-прежнему определяется формулой k = со/с, где с = (dp/dp)^1/2, причем производная др/др равна выражению (81,3). (Величина с не имеет, однако, теперь смысла скорости звука уже хотя бы потому, что она комплексна.) Таким обра­зом, получаем:

k

(81,8)

Определяемый этой формулой «волновой вектор» является величиной комплексной. Легко выяснить смысл этого обстоя­тельства. В плоской волне все величины зависят от координаты х (в направлении распространения) посредством множителя е^1кк. Написав k в виде k = ki -f- ik₂ с вещественными k\ и k₂, полу­чаем _e^ikx'==e^lkiX(!~^klX, т. е. наряду с периодическим множителем _eik_xx получается также затухающий множитель е~^к'^х (k₂ долж­но быть, конечно, положительным). Таким образом, комплекс­ность волнового вектора является формальным выражением того, что волна затухает, т. е. имеет место поглощение звука. При этом вещественная часть комплексного «волнового век­тора» определяет изменение фазы волны с расстоянием, а мни­мая его часть есть коэффициент поглощения.

Нетрудно отделить в (81,8) вещественную и мнимую части; в общем случае произвольных о> выражения для k\ и k₂ довольно громоздки, и мы не выписываем их здесь. Существенно, что k\ (как и k₂) является функцией частоты. Таким образом, если в жидкости могут происходить химические реакции, то распростра­нение звука с достаточно большими частотами) сопровождается дисперсией.

В предельном случае малых частот (шт <С 1) формула (81,8) дает в первом приближении k = со/с₀, что соответствует рас­пространению звука со скоростью Со. Так, разумеется, и должно было быть: условие от <С 1 означает, что период 1/ш звуковой волны велик по сравнению со временем релаксации; другими словами, установление химического равновесия практически ус­певает следовать за колебаниями плотности в звуковой волне, и поэтому скорость звука должна определяться равновесной производной {др/ф)_Равн. В следующем приближении имеем:

* = — + t^-(ol-ct), (81,9)

т. е. появляется затухание с коэффициентом, пропорциональным квадрату частоты. С помощью (81,7) мнимую часть k можно написать в виде k₂ = e>%₀/2pcl; это совпадает с зависящей от £ частью коэффициента поглощения y (79,6), полученного без учета дисперсии.

В обратном предельном случае больших частот (сот^>1) имеем в первом приближении k = со/Со, т. е. распространение звука со скоростью с_х — результат опять-таки естественный, по­скольку при сот ^> 1 можно считать, что за время одного периода реакция вовсе не успевает произойти; поэтому скорость звука должна определяться производной (др/др)%, взятой при постоян­ных концентрациях. В следующем приближении имеем:

* = — + (81,10)

Коэффициент поглощения оказывается не зависящим от частоты. При переходе от и<1Д к«>1/т этот коэффициент моно­тонно возрастает, стремясь к постоянному значению, определяе­мому формулой (81,10). Заметим, что величина k₂/k\, характе­ризующая поглощение на расстоянии, равном длине волны, ока­зывается в обоих предельных случаях малой (k₂/k\ -С 1); она имеет максимум при некоторой промежуточной частоте (равной

©т = УСо/О-

Уже из формулы, например, (81,7) видно, что

с_ж>с₀ (81,11)

(поскольку должно быть £>0). В том же самом можно убе­диться с помощью простых рассуждений на основании принципа Ле-Шателье.

Предположим, что под влиянием внешнего воздействия объем системы уменьшается (а плотность увеличивается). Этим си­стема выводится из состояния равновесия, и согласно принципу Ле-Шателье в ней должны начаться процессы, стремящиеся уменьшить давление. Это значит, что величина др/др будет уменьшаться, и когда система вновь вернется в состояние рав­новесия, значение др/др — с² будет меньшим, чем оно было в не­равновесном состоянии.

При выводе всех формул мы предполагали, что имеется всего один медленный внутренний процесс релаксации. Возможны так­же и случаи, когда имеется одновременно несколько различных таких процессов. Все формулы могут быть без труда обобщены на такой случай. Вместо одной величины £ мы будем иметь те­перь ряд величин |_ь 1₂, • ■ •, характеризующих состояние тела, и соответственно ряд времен релаксации ть х₂,... Выберем вели­чины |„ таким образом, чтобы каждая из производных |„ зави­села только от соответствующего |„, т. е. чтобы было

= <!„-&)»). (81,12)

ЗВУК

[гл. vihj

Вычисления, вполне аналогичные предыдущим, приводят тогда к формуле

п

где = (-3^-). ^а постоянные а_п равны

При всего одной величине g эта формула, как и должно быть, переходит в формулу (81,3),

ГЛАВА IX

УДАРНЫЕ ВОЛНЫ

§ 82. Распространение возмущений в потоке сжимаемого газа

Когда скорость движения жидкости делается сравнимой со скоростью звука или превышает ее, на передний план выдви­гаются эффекты, связанные с сжимаемостью жидкости. С такого рода движениями приходится на практике иметь дело у газов. Поэтому о гидродинамике больших скоростей говорят обычно как о газодинамике.

Прежде всего следует заметить, что в газодинамике практи­чески всегда приходится иметь дело с очень большими значе­ниями числа Рейнольдса. Действительно, кинематическая вяз­кость газа, как известно из кинетической теории газов, — по­рядка величины произведения длины свободного пробега моле­кул / на их среднюю скорость теплового движения; последняя же совпадает по порядку величины со скоростью звука, так что v ~ cl. Если характеристическая скорость газодинамической за­дачи — порядка величины скорости звука или больше, то число Рейнольдса R ~ Lu/v ~ Lu/lc, т. е. содержит заведомо очень большое отношение характеристических размеров L к длине сво­бодного пробега /'). Как всегда, при очень больших значениях R вязкость оказывается не существенной для движения газа практически во всем пространстве, и в дальнейшем мы везде (за исключением лишь особо оговоренных мест) рассматриваем газ как идеальную (в гидродинамическом смысле слова) жидкость.

Движение газа имеет существенно различный характер в за­висимости от того, является ли оно дозвуковым или сверхзвуко­вым, т. е. меньше или больше его скорость, чем скорость звука. Одним из наиб.олее существенных принципиальных отличий сверхзвукового потока является возможность существования в нем так называемых ударных волн, свойства которых будут подробно рассмотрены в следующих параграфах. Здесь же мы рассмотрим другую характерную особенность сверхзвукового движения, связанную со свойствами распространения в газе ма­лых возмущений.

') Мы не рассматриваем вопроса о движении тел в очень разреженных газах, в которых длина пробега молекул сравнима с размерами тел. Этот вопрос по существу не является гидродинамической проблемой и должен рассматриваться с помощью кинетической теории газов.

Если в каком-нибудь месте стационарно движущийся газ под­вергается слабому возмущению, то влияние этого возмущения распространяется затем по газу со скоростью (относительно са­мого газа), равной скорости звука. Скорость же распростране­ния возмущения относительно неподвижной системы координат складывается из двух частей: во-первых, возмущение сносится потоком газа со скоростью v и, во-вторых, распространяется от­носительно газа со скоростью с в некотором направлении п. Рас­смотрим для простоты однородный плоско-параллельный поток газа с постоянной скоростью v. Пусть в некоторой (неподвиж­ной в пространстве) точке О газ подвергается малому возмуще­нию. Скорость v + сп распространения исходящего из точки О возмущения (относительно неподвижной системы координат) различна в зависимости от направления единичного вектора п. Все возможные ее значения мы получим, отложив из точки О вектор v, а из его конца, как из центра, построив сферу радиуса с; векторы, проведенные из О в точки этой сферы, и определят

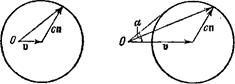
возможные величины и
направления скорости
распространения возму-
щения. Предположим сна-
чала, что о < с. Тогда
векторы v + сп могут
иметь любое направле-
а) 6) ние в пространстве

(рис. 50, а). Другими сло-
^Рис- ⁵⁰ вами, в дозвуковом пото-

ке возмущение, исходя­щее из некоторой точки, распространяется в конце концов по всему газу. Напротив, в сверхзвуковом потоке, и > с, направления векторов v+cn, как видно из рис. 50,6, могут ле­жать только внутри конуса с вершиной в точке О, касающегося построенной из конца вектора v, как из центра, сферы. Для угла раствора 2а этого конуса имеем, как видно из чертежа:

sin а == с/и. (82,1)

Таким образом, в сверхзвуковом потоке исходящее из некоторой точки возмущение распространяется только вниз по течению внутри конуса с углом раствора тем меньшим, чем меньше отно­шение c/v. На всей области потока вне этого конуса возмущение в точке О не отразится вовсе.

Определяемый равенством (82,1) угол называют углом Маха. Отношение же v/c, весьма часто встречающееся в газодинамике, называют числом Маха:

М = v/c.

(82,2)

Поверхность, ограничивающую область, которую достигает ис­ходящее из заданной точки возмущение, называют поверхностью Маха или характеристической поверхностью.

В общем случае произвольного стационарного течения эта поверхность не является уже конической во всем объеме потока. Можно, однако, по-прежнему утверждать, что она пересекает в каждой своей точке линию тока под углом, равным углу Маха. Значение же угла Маха меняется от точки к точке соответствен­но изменению скоростей у и с. Подчеркнем здесь, кстати, что при движении с большими скоростями скорость звука различна в разных местах газа —она меняется вместе с термодинамиче­скими величинами (давлением, плотностью и т. д.), функцией которых она является¹). О скорости звука как функции коорди­нат точки говорят как о местной скорости звука.

Описанные свойства сверхзвукового течения придают ему ха­рактер, совершенно отличный от характера дозвукового движе­ния. Если дозвуковой поток газа встречает на своем пути ка­кое-либо препятствие, например, обтекает какое-либо тело, то наличие этого препятствия изменяет движение во всем простран«стве как вверх, так и вниз по течению; влияние обтекаемого те­ла исчезает лишь асимптотически при удалении от тела. Сверхзву­ковой же поток натекает на пре­пятствие «слепо»; влияние обте­каемого тела простирается лишь на область вниз по течению²), а во всей остальной области пространства вверх по тече­нию газ движется так, как если бы никакого тела вообще не было.

') При изучении звуковых волн в главе VIII мы могли считать скорость звука постоянной. ²) Во избежание недоразумений оговорим, что если перед обтекаемым телом возникает ударная волна, то эта область несколько увеличивается (см. § 122).

В случае плоского стационар-
ного течения газа вместо харак- А
теристических поверхностей мож- Рис. 61
но говорить о характеристиче-
ских линиях (или просто характеристиках) в плоскости движе-
ния. Через всякую точку О этой плоскости проходят две харак-
теристики (АА' и ВВ' на рис. 51), пересекающие проходящую
через эту же точку линию тока под углами, равными углу Маха.
Ветви OA и ОВ характеристик, направленные вниз по течению,
можно назвать исходящими из точки О; они ограничивают об-
ласть АОВ течения, на которую могут влиять исходящие из

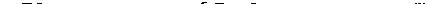
и уравнение непрерывности:

+ vV6p + рс² div 6v = 0 (3)

(здесь подставлено 6р = с~²Ьр + (dp/ds)_p 6s; члены с 6s выпадают в силу (2)). Для возмущения вида ехр [('(kr — at)] находим систему алгебраических уравнений:

(vk — со) 6s = 0, (vk — со) 6v + к бр/р = О, (vk — со) 6р + рс²к 6v = 0.

Отсюда видно, что возможны два вида возмущений. В одном из них (энтропийно-вихревая волна)

co = vk, 6s Ф 0, бр = 0, 6p = ^-|^-^6s, k6v = 0;

отлична от нуля также и завихренность rot 6v = i[k8v]. Возмущения 6s и Sv в этой волне независимы. Равенство со = vk означает перенос возмущения движущимся газом.

В другом типе возмущений

(со- vk)² = c²£², 6s = 0, 6р = с²6р,

(со — vk) бр = pc²k 6v, [к 6v] = 0.

Это — звуковая волна с частотой, сдвинутой эффектом Доплера. Задание возмущения одной из величин в этой волне определяет возмущения всех остальных величин.

§ 83. Стационарный поток сжимаемого газа

Уже непосредственно из уравнения Бернулли можно получить ряд общих результатов, касающихся произвольного адиабати­ческого стационарного движения сжимаемого газа. Уравнение Бернулли для стационарного движения гласит

Дата добавления: 2014-11-07