Ol — V2X 57 страница

') Так, в двухатомных газах при температурах позади ударной волны порядка 1000—3000 К медленным релаксационным процессом является возбу­ждение внутримолекулярных колебаний. При более высоких температурах роль такого процесса переходит к термической диссоциации молекул на со­ставляющие их атомы,

(после /) реальной точкой является точка /', отвечающая со­стоянию с вовсе несмещенным относительно состояния / релак­сационным равновесием. Сжатие газа п, от состояния / до состояния У совер­шается скачком, вслед за чем уже про­исходит (на расстояниях ~v\\) посте­пенное сжатие до конечного состоя­ния 2'

Если равновесная и неравновесная ударные адиабаты пересекаются (рис. 68), появляется возможность существо­вания ударных волн еще одного типа: если скорость волны такова, что хорДа 12 пересекает адиабаты выше точки их взаимного пересечения (как на рис.68), то релаксация будет сопровождаться понижением давления — от значения, отвечающего точке /' до значения, (С. П. Дьяков, 1954)').

% 95. Изотермический скачок

Рассматривая в § 93 строение ударной волны, мы по суще­ству предполагали, что коэффициенты вязкости и температуро­проводности — величины одного порядка, как это обычно и бы­вает. Возможен, однако, и случай, когда % ^> v. Именно, если температура вещества достаточно высока, то в теплопроводности будет участвовать добавочный механизм — лучистая теплопро­водность, осуществляемая находящимся в равновесии с веще­ством тепловым излучением. На вязкости же (т. е. на переносе импульса) наличие излучения сказывается в несравненно мень­шей степени, в результате чего v и может оказаться малым по сравнению с %. Мы увидим сейчас, что наличие такого неравен­ства приводит к весьма существенному изменении^ структуры ударной волны.

Пренебрегая членами, содержащими вязкость, напишем урав­нения (93,2) и (93,3), определяющие структуру переходного слоя,в виде

P + i²V = p_l + j²V_l, (95,1)

у, dT /V /V?

') Такой случай мог бы, в принципе, иметь место в диссоциирующем многоатомном газе, если в равновесном состоянии за ударной волной дости­гается достаточно полная диссоциация его молекул на меньшие части. Дис­социация увеличивает значение отношения теплоемкостей у, и тем самым уменьшает предельное сжатие в ударной волне, если только она уже на­столько полна, что нагревание газа не требует заметной затраты энергии на продолжение диссоциации.

Правая сторона второго из этих уравнений обращается в нуль лишь на границе слоя. Поскольку температура позади ударной волны должна быть выше, чем впереди нее, то отсюда следует, что на протяжении всей ширины переходного слоя

4j>0, (95,3)

т. е. температура возрастает монотонно.

Все величины в слое являются функцией одной переменной — координаты х, а потому и определенными функциями друг от друга. Продифференцировав соотношение (95,1) по V, получим:

(ja-s+(ia+<*=»■

Производная (dp/dT)_v у газов всегда положительна. Поэтому знак производной dT/dV определяется знаком суммы (др/дV) т + + /². В состоянии 1 имеем /² > — (dpi/dV\)_s (так как v\ > й), а поскольку адиабатическая сжимаемость всегда меньше изо­термической, то во всяком случае и

?>-(Ш-

Следовательно, на стороне 1 производная

ilL <₀ dVi ^

Если эта производная отрицательна и на всем протяжении ши­рины переходного слоя, то по мере сжатия вещества (уменьше­ния V) при переходе со стороны 1 на сторону 2 температура будет монотонно возрастать в согласии с неравенством (95,3). Другими словами, мы будем иметь дело с ударной волной, силь­но расширенной благодаря большой теплопроводности (расши­рение может оказаться столь большим, что самое представление об ударной волне станет условным). Другая ситуация возникает, если

?<-{Ш <⁹⁵>⁴>

(это неравенство отвечает достаточно большой интенсивности ударной волны — см. ниже (95,7)). Тогда в состоянии 2 будем иметь dT₂/dV2, так что где-то между значениями V — Vi и V = У₂ функция T(V) будет иметь максимум (рис. 69). Ясно, что переход от состояния 1 к состоянию 2 с непрерывным изме­нением V станет невозможным, так как при этом неизбежно на­рушилось бы неравенство (95,3).

В результате мы получим следующую картину перехода от начального состояния / к конечному состоянию 2. Сначала идет область, в которой происходит постепенное сжатие вещества от

удельного объема V\ до объема V (значение V, при котором впервые становится T(V') = T₂; см. рис. 69); ширина этой об­ласти, определяющаяся теплопроводностью, может быть весьма значительной. Сжатие же от V до V2 происходит затем скачком лри постоянной (равной Т₂) температуре. Этот разрыв можно назвать изотермическим скачком.

Определим изменения давле­ния и плотности в изотермическом скачке, предполагая газ идеаль­ным. Условие непрерывности по­тока импульса (95.1), применен­ное к обоим сторонам скачка, дает

p' + i²v' = P2 + i²v₂.

Для термодинамически идеально­го газа пишем V = RT/цр и, имея а виду, что Т' = Т₂, получим:

Р + Ч^Г- = Рг +

цр • < • цр₂

Это квадратное уравнение для р' имеет (помимо тривиального корня р' = р₂) решение

Р =

fⁱRT₂

W2

■PV₂.

(95,5)

Выражаем j² согласно формуле (85,6):

V₂,

Pi — Pi

^r V\ — V₂

после чего, подставив сюда V₂/Vi из (89,1), получим для поли­тропного газа

(95,6)

p' = ii(Y+l)Pi+(Y-l)p₂].

Поскольку должно быть р₂ > р', то мы находим, что изотерми­ческий скачок возникает лишь при отношениях давлений р₂ и Pi, удовлетворяющих условию

Pi

(95,7)

3-у "

{Rayleigh, 1910). Это условие можно, конечно, получить и не­посредственно из (95,4).

(95,8)

Поскольку при данной температуре плотность газа пропор­циональна давлению, то отношение плотностей в изотермиче­ском скачке равно отношению давлений:

р₂ V р₂

а стремится три увеличении рг к значению (у—1)/2.

§ 96. Слабые разрывы

Наряду с поверхностями разрывов, на которых испытывают скачок величины р, р, v и т. п., могут существовать также и та­кие поверхности, на которых эти величины как функции коорди­нат обладают какими-либо особенностями, оставаясь сами не­прерывными. Эти особенности могут быть самого разнообраз­ного характера. Так, на поверхности разрыва могут испытывать, скачок первые производные по координатам от величин р, р, v,... или же эти производные могут обращаться в беско­нечность. Наконец, то же самое может иметь место для произ­водных не первого, а более высоких порядков. Все такие поверх­ности мы будем называть поверхностями слабого разрыва в про­тивоположность сильным разрывам (ударным волнам и танген­циальным разрывам), в которых испытывают скачок сами ука­занные величины. Отметим, что ввиду непрерывности самих этих величин на поверхности слабого разрыва, непрерывны также и их тангенциальные производные; разрыв непрерывности испыты­вают лишь нормальные к поверхности производные.

Легко убедиться простыми рассуждениями, что поверхности слабого разрыва распространяются относительно газа (по обе стороны поверхности) со скоростью, равной скорости звука. Дей­ствительно, поскольку функции р, р, v,... сами не испытывают скачка, то их можно сгладить, заменив функциями, совпадаю­щими с ними везде, кроме окрестности поверхности разрыва, а в этой окрестности отличающимися лишь на сколь угодно ма­лые величины, но так, что сглаженные функции не имеют уже-никаких особенностей. Истинное распределение, скажем, давле­ния, можно, таким образом, представить в виде наложения со­вершенно плавного распределения р₀ без всяких особенностей и очень малого нарушения р' этого распределения вблизи поверх­ности разрыва. Последнее же, как и всякое малое возму­щение, распространяется относительно газа со скоростью звука.

Подчеркнем, что в случае ударной волны сглаженные функ­ции отличались бы от истинных на величины, вообще говоря, от­нюдь не малые, и предыдущие рассуждения поэтому неприме­нимы. Однако если скачок величин в ударной Волне достаточно мал, то эти рассуждения вновь делаются применимыми, и такие разрывы тоже должны распространяться со скоростью звука, — этот результат был уже получен в § 86 другим способом.

Если движение стационарно относительно данной системы координат, то поверхность разрыва неподвижна относительно этой системы, а газ протекает через нее. При этом нормальная к поверхности разрыва компонента скорости газа должна быть равна скорости звука. Если обозначить посредством а угол между направлением скорости газа и касательной плоскостью

к поверхности, то должно быть v„ = v sin а = с, или

sin а = c/v,

т. е. поверхность слабого разрыва пересекает линию тока под углом Маха. Другими словами, поверхность слабого разрыва совпадает с одной из характеристических поверхностей, — ре­зультат вполне естественный, если иметь в виду физический смысл последних как поверхностей, вдоль которых распростра­няются малые возмущения (§ 82). Ясно, что при стационарном движении газа слабые разрывы могут появиться только при ско­ростях, равных или превышающих скорость звука.

В отношении способов возникновения слабые разрывы су­щественно отличаются от сильных. Мы увидим, что ударные вол­ны могут образовываться сами по себе, непосредственно в ре­зультате движения газа, при непрерывных граничных условиях (например, образование ударных волн в звуковой волне; § 102). В противоположность им слабые разрывы не могут возникать сами по себе; их появление всегда связано с какими-либо осо­бенностями в граничных или начальных условиях движения. Особенности эти могут быть, как и сами слабые разрывы, са­мого различного характера. Так, причиной образования слабого-разрыва может являться наличие углов на поверхности обтекае­мого тела; на возникающем в этом случае слабом разрыве ис­пытывают сцзчок первые производные скорости по координатам. К образованию слабого разрыва приводит также и скачок кри­визны поверхности тела без угла на ней (причем испытывают разрыв вторые производные скорости по координатам) и т. п. Наконец, всякая особенность в изменении движения со временем влечет за собой возникновение нестационарного слабого разрыва.

Касательная к поверхности слабого разрыва компонента ско­рости протекающего через нее газа направлена всегда по на­правлению от того места (например, угла на поверхности тела), откуда исходят возмущения, вызывающие возникновение этого-разрыва; мы будем говорить, что разрыв «исходит» из этого ме­ста. Это есть одно из проявлений направленности распростране­ния возмущений вниз по течению в сверхзвуковом потоке.

Наличие вязкости и теплопроводности приводит к возникно­вению ширины у слабого разрыва, так что слабые разрывы, как и сильные, представляют собой в действительности некоторые пе­реходные слои. Однако в отличие от ударных волн, ширина ко­торых зависит только от их интенсивности и постоянна во вре­мени, ширина слабого разрыва растет со временем, начиная с момента образования разрыва. Закон, по которому происходит-это возрастание, легко найти (качественно) исходя из аналогии между перемещением слабого разрыва и распространением малых звуковых возмущений. При наличии вязкости и тепло­проводности возмущение, сконцентрированное первоначально­

в малом элементе объема (волновой пакет), по мере своего пе­ремещения с течением времени расширяется; закон этого расши­рения был определен в § 79. Из него можно сразу заключить, что ширина б слабого разрыва

б~(ас³*)^1/2, (96,1)

где t — время, прошедшее с момента его возникновения, а о — коэффициент при квадрате частоты в формуле (79,6) для поглощения звука. Если мы имеем дело со стационарной карти­ной, в которой разрыв покоится, то вместо времени t надо го­ворить о расстоянии / от места, из которого исходит разрыв (например, для слабого разрыва, возникающего от угла на по­верхности обтекаемого тела, / есть расстояние от вершины угла); тогда б ~ (ас²1)^1/21).

') Подчеркнем, однако, что для количественного определения структуры слабого разрыва аналогия со звуком была бы недостаточна. Дело в том, что при определении закона затухания звука его амплитуду можно предполагать сколь угодно малой и соответственно этому исходить из линеаризованных уравнений движения. Для слабых же разрывов (как и для ударных волн «слабой интенсивности — § 93) должна учитываться нелинейность уравнений, поскольку без нее отсутствовали бы и самые разрывы. Пример такого иссле­дования дан в задаче 6 к § 99. ²) Слабый разрыв ротора, скорости означает слабый разрыв касательной к поверхности компоненты скорости. Например, могут испы ьгвать скачок взя­тые по направлению к нормали к поверхности производные от тангенциальной •скорости.

В заключение этого параграфа необходимо сделать замеча­ние, аналогичное замечанию в конце § 82. Там было отмечено, что среди различных возмущений состояния движущегося газа исключительными по своим свойствам являются возмущения энтропии (при постоянном давлении) и ротора скорости. Эти возмущения покоятся относительно газа, а не распространяются -со скоростью звука. Поэтому поверхности, на которых испыты­вают какой-либо слабый разрыв непрерывности энтропия и ро­тор'скорости²), покоятся относительно газа, а относительно не­подвижной системы координат переносятся вместе с самим газом. Такие разрывы мы будем называть тангенциальными сла­быми разрывами; они проходят через линии тока и в этом отно­шении вполне аналогичны «сильным» тангенциальным разрывам.

ГЛАВА X

ОДНОМЕРНОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА

§ 97. Истечение газа через сопло

Рассмотрим стационарное вытекание газа из большого со­суда через трубку переменного сечения, или, как говорят, через сопло. Мы будем предполагать, что движение газа можно счи­тать в каждом месте трубы однородным по ее сечению, а ско­рость— направленной практически вдоль оси трубы. Для этого-труба должна быть не слишком широка, и площадь S ее сече­ния должна достаточно медленно меняться вдоль ее длины. Та­ким образом, все величины, характеризующие течение, будут функциями только от координаты вдоль оси трубы. При этих условиях можно применять полученные в § 83 соотношения, имеющие место вдоль линии тока, непосредственно к изменению величин вдоль длины трубы.

Количество (масса) газа, проходящего в единицу времени через поперечное сечение трубы, или, как говорят, расход газа, равно Q = pvS; эта величина должна, очевидно, оставаться по­стоянной вдоль всей трубы:

Q = Spy = const: (97,1)

Линейные размеры самого сосуда предполагаются очень боль­шими по сравнению с диаметром трубы. Поэтому скорость газа в сосуде можно считать равной нулю, и соответственно этому все величины с индексом нуль в формулах § 83 будут представлять, собой значения соответствующих величин внутри сосуда.

Мы видели, что плотность потока / = pv не может превы­шать некоторого предельного значения /„. Ясно поэтому, что и возможные значения полного расхода газа Q будут иметь (для данной трубы и при заданном состоянии газа внутри сосуда) верхнюю границу Qmax, которую легко определить. Если бы зна­чение /» плотности потока было достигнуто не в самом узком месте трубы, то в сечениях с меньшим S было бы / >> /„, что не­возможно. Поэтому значение / = /» может быть достигнуто толь­ко в самом узком месте трубы, площадь сечения которого обо­значим посредством S_mm. Таким образом, верхняя граница пол­ного расхода газа есть

Qmax «Р.»Лп1п = (j^j) ⁵mln. (97,2>

Рассмотрим сначала сопло, монотонно суживающееся по на-
правлению к своему внешнему концу, так что минимальная пло-
щадь сечения достигается на этом конце (рис. 70). В силу (97,1)
плотность потока / монотонно возрастает вдоль трубы. То же
самое касается скорости газа о, а давление соответственно моно-
тонно падает. Наибольшее возможное значение / будет достиг-
У нуто, если скорость v достигает значе-

^; ния с как раз на выходном конце тру-

'⁴^&2a&-v_/. бы, т. е. если будет V\ ~ С\ = и* (бук-

I ^^^^^Ш2^А^ вы с индексом 1 обозначают значения

-I----------------- —Х ------------ '\-^т величин на выходном конце трубы).

' '\777^^77777Щ Одновременно будет и р = р,.
^гт^р^^ Проследим за изменением режима

^ вытекания газа при уменьшении давле-

^//-ния р_е внешней среды, в которую газ

Рис. 70 выпускается. При уменьшении внеш-

него давления от значения, равного давлению ро в сосуде, и вплоть до значения р* одновременно с ним падает также и давление pi в выходном сечении трубы, причем оба эти давления (pi и р_е) остаются равными друг другу; дру­гими словами, вс > падение давления от р₀ до внешнего проис­ходит внутри сопла. Выходная же скорость v\ и полный расход газа Q =/i5mi_n монотонно возрастают. При р_е = р_<. выходная скорость делается равной местному значению скорости звука, а расход газа — значению Qmax- При дальнейшем понижении внеш­него давления выходное давление перестает падать и остается все время равным р»; падение же давления от р_ф до р_е про­исходит уже вне трубы, в окружающем пространстве. Другими словами, ни при каком внешнем давлении падение давления газа в трубе не может быть большим, чем от р₀ до р»; так, для воз­духа (р* = 0,53 ро) максимальное падение давления составляет 0,47 р₀. Выходная скорость и расход газа тоже остаются (при

Ре < р*) постоянными. Таким обра-
зом, при истечении через суживаю-
_v ^£ ^^///////л. шееся сопло газ не может приоб-
^2^^ ^^^ | рести сверхзвуковой скорости.
ssftTTzfy^^^ Невозможность достижения

i ^Sm 4 сверхзвуковых скоростей при выпу-

^ екании газа через суживающееся

Р_ИС. 71 сопло связана с тем, что скорость,

равная местной скорости звука, мо­жет достигаться только на самом выходйом конце такой трубы. Ясно, что сверхзвуковая скорость сможет быть достигнута с по­мощью сопла сначала суживающегося, а затем вновь расширяю­щегося (рис. 71). Такие сопла называются соплами Лаваля.

Максимальная плотность потока /„, если и достигается, то -опять-таки только в наиболее узком сечении, так что и в таком

сопле расход газа не может превышать значения 5min/». В су­живающейся части сопла плотность потока возрастает (а дав­ление падает); на кривой рис. 72, изображающей зависимость / от р¹), это соответствует передвижению от точки с по направле­нию к Ь. Если в сечении S_m\n достигается максимальный поток (точка b на рис. 72), то в расширяющейся части сопла давле­ние будет продолжать падать и начнет падать также и / соот­ветственно перемещению по •

кривой рис. 72 от точки b по направлению к а. На выход­ном конце трубы поток / при­обретает тогда вполне опреде­ленное значение, равное

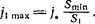
а давление — соответствующее этому потоку значение, обозна­ченное на рис. 72 посредством р\ (некоторая точка d на кри­вой). Если же в сечении Smm достигается лишь некоторая точ­ка е, то в расширяющейся части сопла давление будет возра­стать соответственно обратному перемещению по кривой вниз от точки е. На первый взгляд могло бы показаться, что с ветви cb кривой можно перейти на ветвь ab скачком, минуя точку Ь, посредством образования ударной волны; это, однако, невоз­можно, так как «втекающий» в ударную волну газ не может иметь дозвуковой скорости.

Имея в виду все эти замечания, проследим теперь за измене­нием режима вытекания по мере постепенного увеличения внеш­него давления р_е. При малых давлениях, начиная от нуля и до значения р_е = р', устанавливается режим, при котором в сече­нии Smin достигается давление р* и скорость у„ = с». В расши­ряющейся части сопла скорость продолжает расти, так что осу­ществляется сверхзвуковое течение газа, а давление продол­жает соответственно падать, достигая на выходном конце зна­чения р\ вне зависимости от величины р_е. Падение давления от Pi до р_е происходит вне сопла, в отходящей от края его отвер­стия волне разрежения (как это будет описано в § 112).

/ =

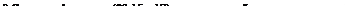Когда р_е начинает превышать значение р\, появляется отхо­дящая от края отверстия сопла косая ударная волна, сжимаю­щая газ от выходного давления р' до давления р_е (§ 112). Мы увидим, однако, что стационарная ударная волна может отхо­дить от твердой поверхности лишь постольку, поскольку она не обладает слишком большой интенсивностью (§ 111). Поэтому при дальнейшем повышении внешнего давления ударная волна скоро начинает передвигаться внутрь сопла, причем перед ней, на вчутренней поверхности сопла, возникает отрыв. При некото­ром значении р_е ударная волна достигает наиболее узкого сече­ния сопла и затем исчезает; течение становится всюду дозвуко­вым с отрывом на стенках расширяющейся (диффузорной) части сопла. Все эти сложные явления имеют уже, разумеется, суще­ственно трехмерный характер.

Задача

На малом участке длины трубы к стационарно текущему по ней газу подводится небольшое количество тепла. Определить изменение скорости газа при прохождении им этого участка. Газ предполагается политропным.

Решение. Пусть Sq есть подводимое в единицу времени количество тепла (S — площадь сечения трубы в данном ее участке). На обеих сторонах участка подогрева одинаковы плотности потока массы / = ро и потока им­пульса р + jv; отсюда Др = — /До, где Д обозначает изменение величины при прохождении этого участка. Разность же плотностей потока энергии (w -f- v²/2) / равна q. Написав w в виде

_ш= урур°

(Y-DP (Y-D/ ' получим (считая До и Др малыми):

°1^Ао + у — 1 <Р ^Ло + ⁰ М =* ч-Исключая Др из этих двух соотношений, найдем:

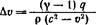
Мы видим, что при дозвуковом течении подвод тепла ускоряет поток (До > 0), а при сверхзвуковом—замедляет.

Написав температуру газа в виде Т = \iplRp = V^pv/Rj (R — газовая по­стоянная), найдем для ее изменения выражение

дг =-£-₍,Др + рд») = ЩТ¹⁾1(—-"²У

Rl Rj (с² — о²) V Y /

При сверхзвуковом движении это выражение всегда положительно — темпе­ратура газа повышается; при дозвуковом же движении оно может быть как положительным, так и отрицательным.

§ 98. Вязкое движение сжимаемого газа по трубе

Рассмотрим течение сжимаемого газа по трубе (постоянного сечения) настолько длинной, что нельзя пренебрегать трением газа о стенки, т. е. вязкостью газа. Стенки трубы мы будем предполагать теплоизолированными, так что никакого обмена теплом между газом и внешней средой не происходит.

При скоростях течения порядка или превышающих скорость звука (о которых только и идет здесь речь) течение газа по трубе является, конечно, турбулентным (если только радиус тру­бы не слишком мал). Турбулентность движения будет суще­ственна здесь для нас только в одном отношении. Именно, мы видели в § 43, что при турбулентном течении скорость (сред­няя) практически постоянна почти по всему сечению трубы и быстро падает до нуля лишь на очень близких расстояниях от стенок. На этом основании мы будем считать скорость течения v просто постоянной по всему сечению трубы, определив ее так, чтобы произведение Spv (S— площадь сечения) было равно полному расходу газа через сечение трубы.

Поскольку полный расход газа Spv постоянен вдоль всей длины трубы, a S постоянно по предположению, то должна быть постоянной также и плотность потока газа

/ = pv = const. (98,1)

Далее, поскольку труба теплоизолирована, то вдоль нее должен быть постоянным также и полный поток энергии, переносимой газом через поперечное сечение трубы. Этот поток равен Spv(w -f- v²/2), и ввиду (98,1) можно написать:

w + -у- = w + = const. (98,2)

Что же касается энтропии газа s, то благодаря наличию внут­реннего трения она, конечно, отнюдь не остается постоянной, а возрастает по мере движения газа вперед по трубе. Если х— координата вдоль оси трубы, причем положительное направле­ние оси х совпадает с направлением течения, то

% > °- (⁹⁸'3)

Продифференцируем теперь соотношение (98,2) по л. Помня, что dw = Т ds + V dp, имеем:

¹ dx ^{T v} dx ^ ^{1 v} dx ^u" Далее, подставляя сюда

dx \ dp)_s dx ^ \ ds)_p dx ' ^(yQ'^v

получаем:

"[>+<4f).]£- <ад

Согласно известной термодинамической формуле (QV \ ₌_Т_ (дУ\ Us)_р~ с_р \дТ)_р-

Коэффициент теплового расширения газов положителен. По­этому в силу (98,3) заключаем, что положительно также и все выражение в левой стороне равенства (98,5). Знак же производ­ной dp/dx совпадет, следовательно, со знаком выражения

-['+/■(£).]-£-'■

Мы видим, что

-g-<0 при v<c, |f->0 при v>c. (98,6)

Таким образом, при дозвуковом течении Давление падает вниз по течению (как и для несжимаемой жидкости). При сверхзву­ковом же движении давление возрастает вдоль трубы.

Аналогичным образом можно установить знак производной dv/dx. Ввиду того, что j = v/V — const, знак dv/dx совпадает со знаком производной dV/dx. Последняя же может быть вы­ражена через положительную производную ds/dx с помощью (98,4—5). В результате мы найдем, что

■57 > 0 при v<c, < 0 при v > с, (98,7)

т. е. скорость возрастает вниз по течению при дозвуковом и па­дает при сверхзвуковом движении.

Любые две термодинамические величины текущего вдоль трубы газа являются функциями друг от друга, совершенно не зависящими, в частности, от закона сопротивления трубы. Эти функции зависят как от параметра от значения постоянной / и определяются уравнением ш -+- j²V²/2 = const, получающимся путем исключения скорости из уравнений сохранения массы и энергии газа.

Выясним характер, который имеют кривые зависимости, на­пример, энтропии от давления. Переписав (98,5) в виде

-Hl-t

ds __ у с'

мы видим, что в точке, где v = с, энтропия имеет экстремум. Легко видеть, что этот экстремум является максимумом. Дей­ствительно, для значения второй производной от s по р имеем в этой точке:

rf²s I _ ¹ КдрЧ, _Q

(что связано с предполагающейся везде положительностью про­изводной {d²V/dp²)_s\,

Таким образом, кривые зависимости s от р имеют вид, изо­браженный на рис. 73. Справа от максимумов лежит область дозвуковых, а слева — сверхзвуковых скоростей. При увеличе­нии параметра / мы переходим от более высоких к более низко расположенным кривым. Действительно, продифференцировав уравнение (98,2) по / при постоянном р, получим:

s

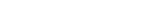Из полученных результатов можно сделать интересный вы­вод. Пусть на входе трубы скорость газа меньше скорости зву­ка. По направлению вниз

¹ С

р

по течению энтропия рас­тет, а давление падает; это соответствует пере­движению по правой вет­ви кривой s = s{p) по на­правлению от В к О (рис. 73). Так может, однако, продолжаться лишь до тех пор, пока энтропия не до­стигнет своего максималь­ного значения. Дальней­шее передвижение по кри­вой за точку О (т. е. в

область сверхзвуковых скоростей) невозможно, так как оно соответствовало бы умень­шению энтропии газа по мере его течения по трубе. Переход с ветви ВО на ветвь OA кривой не может произойти также и посредством возникновения ударной волны, так как скорость «втекающего» в ударную волну газа не может быть дозвуковой.

Дата добавления: 2014-11-07