Должно быть 3 страница

rv = A cos (kr ■

4\ ^ak Л?

In — sin 2 (kr — tat)

(под Г\ надо понимать здесь расстояние, на котором волну можно еще рас­сматривать с достаточной точностью как строго монохроматическую). Второй член в этой формуле определяет вторую гармонику спектрального разложения волны. Ее полная (средняя по времени) интенсивность /₂ равна

8яс³р

К)

где 1\ = 2ясрА² есть интенсивность основной, первой, гармоники.

§ 103. Характеристики

Данное в § 82 определение характеристик как линий, вдоль которых распространяются (в приближении геометрической аку­стики) малые возмущения, имеет общее значение, и не ограни­чено применением к плоскому стационарному сверхзвуковому течению, о котором шла речь в § 82.

Для одномерного нестационарного движения можно ввести характеристики как линии в плоскости х, t, угловой коэффициент которых dx/dt равен скорости распространения малых возму­щений относительно неподвижной системы координат. Возмуще­ния, распространяющиеся относительно газа со скоростью звука в положительном или отрицательном направлении оси х, переме­щаются относительно неподвижной системы со скоростью v + с или v — с. Соответственно дифференциальные уравнения двух семейств характеристик, которые мы будем условно называть характеристиками С+ и С_, гласят:

(■£).— + «• (тг). —«• <¹⁰³''>

Возмущения же, переносящиеся вместе с веществом газа, «рас­пространяются» в плоскости х, t по характеристикам третьего семейства С₀, для которых

(4г)_п = *- <¹⁰³'²>

Это — просто «линии тока» в плоскости к, t (ср. конец § 82)¹). Подчеркнем, что для существования характеристик здесь отнюдь не требуется, чтобы движение газа было сверхзвуковым. Выра­жаемая характеристиками направленность распространения воз­мущений соответствует здесь просто причинной связи движения в последующие моменты времени с предыдущим движением.

В качестве примера рассмотрим характеристики простой вол­ны. Для волны, распространяющейся в положительном направ­лении оси х, имеем согласно (101,5) х== t(v + с)+ f{v). Диффе­ренцируя это соотношение, имеем:

dx = (v + с) dt + dv [t + tc' (v) + f (v) ].

С другой стороны, вдоль характеристики С₊ имеем dx = {v + -\-c)dt; сравнивая оба равенства, найдем, что вдоль характе­ристики dv[t + tc'(v)-r- f'(u)] = 0. Выражение в квадратных скобках не может быть равно нулю тождественно. Поэтому должно быть dv — 0, т. е. v = const. Таким образом, мы при­ходим к выводу, что вдоль каждой из характеристик С+ остается постоянной скорость, а с нею и все остальные величины (в вол­не, распространяющейся влево, таким же свойством обладают характеристики С_). Мы увидим в следующем параграфе, что это обстоятельство не случайно, а органически связано с мате­матической природой простых волн.

Из этого свойства характеристик С+ простой волны можно в свою очередь заключить, что они представляют 'собой семей­ство прямых линий в плоскости х, t; скорость имеет постоянные значения вдоль прямых х — t[v + c(v)\ + /(и) (101,5). В ча­стности, в автомодельной волне разрежения (простая волна с f(v) = 0) эти прямые образуют пучок с общей точкой пересе­чения — началом координат плоскости х, t. Ввиду этого свойства автомодельную простую волну называют центрированной.

На рис. 86 изображено семейство характеристик С+ для про­стой волны разрежения, образующейся при ускоренном выдви­гании поршня из трубы. Это есть семейство расходящихся пря­мых, начинающихся на кривой x = X(t), изображающей движе­ние поршня. Справа от характеристики х = c₀t простирается область покоящегося газа, в которой все характеристики парал­лельны друг другу.

') Точно такими же уравнениями (103,1—2) определяются характеристи­ки и для нестационарного сферически симметричного движения, причем только надо заменить х на сферическую координату т (характеристики будут теперь линиями в плоскости г, t).

На рис. 87 дан аналогичный чертеж для простой волны сжа­тия, образующейся при ускоренном вдвигании поршня в трубу. В этом случае характеристики представляют собой сходящийся пучок прямых, которые в конце концов должны пересечься друг с другом. Поскольку каждая характеристика несет свое постоян­ное значение и, их пересечение друг с другом означает физи­чески бессмысленную многозначность функции v(x, г). Это — гео­метрическая интерпретация результата о невозможности неогра­ниченного существования простой волны сжатия и неизбежности

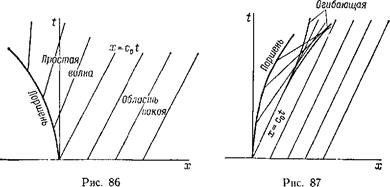
возникновения в ней ударной волны, к которому мы пришли уже аналогичным путем в § 101. Геометрическое же истолкование условий (101,12), определяющих время и место образования ударной волны, заключается в следующем. Пересекающееся се­мейство прямолинейных характеристик имеет огибающую, за­канчивающуюся со стороны малых t угловой точкой, которая и определяет первый момент возникновения многозначности. Если уравнения характеристик заданы в параметрическом виде x = x(v), t = t(v), то положение угловой точки как раз и опре­деляется уравнениями (101,12)').

Покажем теперь коротко, каким образом данное нами физи­ческое определение характеристик как линий распространения возмущений соответствует известному из теории дифференциаль­ных уравнений в частных производных чисто математическому аспекту этого понятия. Рассмотрим уравнение в частных произ-

') Вся область между двумя ветвями огибающей трижды покрыта ха­рактеристиками — в соответствии с трехзначностью величин, возникающей при опрокидывании профиля волны.

Особому случаю, когда ударная волна возникает на границе с областью покоя, соответствует вырождение одной из ветвей огибающей в отрезок ха­рактеристики х — Cot,

водных вида

^ + ^2fiwfr + ^C^+D = 0, (103,3)

линейное по вторым производным (коэффициенты же А, В, С, D могут быть любыми функциями как от независимых переменных х, t, так и от неизвестной функции ф и ее первых производ­ных)¹). Уравнение (103,3) относится к эллиптическому типу, если везде В² — ЛС<0, и к гиперболическому, если В² — — АС > 0. В последнем случае уравнение

Adt² — 2Bdxdt + Cdx² = 0, (103,4)

или

dx В ± л/В* - АС,.

-_dl=--------------- с---------- ' <¹⁰³'⁵⁾

определяет в плоскости х, t два семейства кривых — характери­стик (для заданного решения ц>(х,у) уравнения (103,3)). Ука­жем, что если коэффициенты А, В, С в уравнении являются функциями только от х, t, то характеристики не зависят от конк­ретного решения уравнения.

Пусть данное течение описывается некоторым решением ф = Фо(*, 0 уравнения (103,3), и наложим на него малое воз­мущение фь Это возмущение предполагаем удовлетворяющим условиям, соответствующим геометрической акустике: оно слабо меняет движение (ф! мало вместе со своими первыми производ­ными), но сильно меняется на протяжении малых расстояний (вторые производные от ф] относительно велики). Полагая в уравнении (103,3) ф = фо + Фь получим тогда для ф1 уравнение

причем в коэффициентах А, В, С положено ф = ф₀. Следуя ме­тоду, принятому для перехода от волновой к геометрической оп­тике, пишем ф) в виде ц>\ = ае¹^, где функция tfi (эйконал) — большая величина, и получаем для последней уравнение

*т*+™Ш 3+с(4ГУ-а <шз,б>

Уравнение распространения лучей в геометрической акустике получается приравниванием dx/dt групповой скорости:

dxdm

dt ~~ dk ¹

где

*-й-—-3-

') Для одномерного нестационарного движения уравнению такого вида удовлетворяет потенциал скорости.

Дифференцируя соотношение

Ak² — 2в£со + Ссо² = О,

получим:

dxВ® — Ak

dt ~ Ca — Bk '

а исключая отсюда с помощью того же соотношения k/a>, мы снова придем к уравнению (103,5).

Задача

Найти уравнение второго семейства характеристик в центрированной про­стой волне в политропном газе.

Решение. В центрированной простой волне, распространяющейся в сторону находящегося справа от нее неподвижного газа, имеем:

Vj- = o + с = с₀ + 2—v.

Характеристики С+ изображаются пучком прямых х = const t. Характери­стики же С- определяются уравнением

dx 3 — у х 4

—гг = о — с =;—г- —. г~г ^со-

dt у+ I t у + 1

Интегрируя, находим:

где постоянная интегрирования выбрана так, чтобы характеристика С_ прохо-
дила через точку х = Coto, t = to на характеристике С+ (х граничной
между простой волной и областью покоя.

«Линии тока» в плоскости х, t даются уравнением

dx 2 / х \

-л-°=7+i4t-^c0'

откуда для характеристик Со:

§ 104. Инварианты Римана

Произвольное малое возмущение распространяется, вообще говоря, по всем трем характеристикам (С₊, С_, С₀), исходящим из данной точки плоскости х, t. Можно, однако, разложить про­извольное возмущение на такие части, каждая из которых рас­пространяется лишь по одной из характеристик.

Рассмотрим сначала изэнтропическое движение газа. Напи­шем уравнение непрерывности и уравнение Эйлера в виде

dt ^ ^v дх ^{+ 90} дх ^и> dv, dv. 1 dp _n

в уравнении непрерывности мы заменили производные от плот­ности на производные от давления согласно

ар / ар \ др 1 др др1 dp

~dt ~\др)_s dt ~~~ с² dt ' dx ~~ с² dx '

Разделив первое уравнение на ±рс и сложив его со вторым, получим:

^._±_L_^.₊ f_|L_±_L|__)_(t)±c)_:=o. (104,1)
dt рс dt ¹ V dx — рс dx J^v ' ^v ' '

Далее, введем в качестве новых неизвестных функций величины
= =(104,2)

называемые инвариантами Римана. Напомним, что при изэнтро-пическом движении рис являются определенными функциями от р, и потому стоящие здесь интегралы имеют определенный смысл. Для политропного газа

J₊ = v + -^_rTc, /_ = _w_-A_Tc. (104,3)

После введения этих величин уравнения движения приобре­тают простой вид:

[! + <° + ^с>-£]'₊~⁰-' [ж + ^-^с)^]^/- = °- (¹⁰⁴>⁴>

Дифференциальные операторы, действующие на J+ и пред­ставляют собой не что иное, как операторы дифференцирования в плоскости х, t вдоль характеристик С₊ и С_. Таким образом, мы видим, что вдоль каждой из характеристик С₊ и С_ остается постоянной соответственно величина /+ или Мы можем также сказать, что малые возмущения величины /+ распространяются только вдоль характеристик С₊, а возмущения /_ — вдоль С_.

В общем случае неизэнтропического движения уравнения (104,1) не могут быть написаны в виде (104,4), так как dp/pc не является полным дифференциалом. Эти уравнения, однако, по-прежнему позволяют выделить возмущения, распространяю­щиеся по характеристикам лишь одного семейства. Таковыми являются возмущения вида би ± бр/рс, где 8v и бр — произволь­ные малые возмущения скорости и давления. Распространение

Полная система уравнений движения малых возмущений полу­чается добавлением сюда еще и уравнения адиабатичности

(104,6)

показывающего, что возмущения 6s распространяются вдоль ха­рактеристик С₀. Произвольное малое возмущение всегда можно разложить на независимые части указанных трех видов.

Сравнение с формулой (101,4) показывает, что инварианты Римана (104,2) совпадают с теми величинами, которые в про­стых волнах постоянны вдоль всей области движения в течение всего времени: в простой волне, распространяющейся вправо, постоянно /_, а в волне, бегущей влево, постоянно /₊. С мате­матической точки зрения это есть основное свойство простых волн. Из него следует, в частности, и указанное в предыдущем параграфе свойство — прямолинейность одного из семейств ха­рактеристик. Пусть, например, волна распространяется вправо. Каждая из характеристик С₊ несет свое постоянное значение /₊ и, кроме того, на ней постоянна являющаяся постоянной во всей области величина Но из постоянства двух величин /₊ и У_ следует, что постоянны также и v и р (а с ними и все остальные величины), и мы приходим к найденному в § 103 свойству ха­рактеристик С₊, непосредственно ведущему к их прямолиней­ности.

Если в двух смежных областях плоскости х, t течение описы­вается двумя аналитически различными решениями уравнений движения, то граница между этими областями есть характери­стика. Действительно, эта граница представляет собой разрыв производных каких-либо величин, т. е. некоторый слабый раз­рыв; последние же непременно совпадают с какой-либо характе­ристикой.

Весьма существенное значение в теории изэнтропического од­номерного движения имеет следующее свойство простых волн: течение в области, граничащей с областью постоянного течения (течения с v = const, р = const), есть непременно простая волна.

Доказательство этого утверждения очень просто. Пусть ин­тересующая нас область 1 плоскости х, t граничит справа с об­ластью 2 постоянного течения (рис. 88). В последней, очевидно, постоянны оба инварианта /+ и /_, а оба семейства характери­стик прямолинейны. Граница между обеими областями есть одна из характеристик С+, и линии С₊ одной области не переходят в другую область. Характеристики же С_ непрерывно продол­

жаются из одной области в другую и, покрывая область /, при­носят в нее из области 2 постоянное значение /_. Таким образом, величина /_ будет постоянна и вдоль всей области /, так что по­следняя есть простая волна.

'. Простая волна

Свойство характеристик переносить вдоль себя постоянные значения определенных величин проливает свет на общую по­становку вопроса о задании на­чальных и граничных условий к уравнениям гидродинамики. В различных конкретных физиче­ских задачах выбор этих усло­вий обычно не вызывает сомне­ний и диктуется непосредствен­но физическими соображениями. В более сложных случаях мо­гут, однако, оказаться полезны­ми и чисто математические со­ображения, основанные на об­щих свойствах характеристик.

Будем для определенности говорить об изэнтропическом од­номерном движении газа. С чисто математической точки зрения постановка газодинамической задачи сводится обычно к опреде­лению двух искомых функций (например, v и р) в области пло­скости х, г, лежащей между двумя заданными кривыми (OA и ОВ на рис. 89,а), на которых задаются граничные значения.

Вопрос заключается в том, значения скольких величин должны быть заданы на этих кривых. В этом смысле существенно, как расположена каждая кривая по отношению к направлениям ис­ходящих ') из каждой ее точки двух ветвей характеристик С₊ и С- (показанным на рис. 89 стрелками). Могут представиться два случая: либо оба направления характеристик лежат по одну сторону от кривой, либо кривая расположена между ними. На рис. 89, а кривая OA относится к первому, а ОВ — ко второму случаю. Ясно, что для полного определения искомых функций

') В плоскости х, t «исходящими» из заданной точки ветвями характе­ристик являются ветви, направленные в сторону возрастания t.

в области АО В на кривой OA должны быть заданы значения двух величин (например, обоих инвариантов /₊ и /_), а на кри­вой ОВ — всего одной. Действительно, значения второй вели­чины будут перенесены на кривую ОВ с кривой OA характери­стиками соответствующего семейства и потому не могут быть заданы произвольным образом¹). Аналогично, на рис. 89,б,в изображены случаи, когда на обеих граничных кривых должны быть заданы по одной или по две величины.

Следует также указать, что если граничная кривая совпадает с какой-либо характеристикой, то на ней вообще невозможно произвольное задание двух независимых величин, так как их значения связаны друг с другом одним условием — условием по­стоянства соответствующего инварианта Римана.

Аналогичным образом может быть разобран вопрос о зада­нии граничных условий в общем случае неизэнтропического дви­жения.

Выше мы говорили везде о характеристиках одномерного дви­жения как о линиях в плоскости х, t. Характеристики могут, од­нако, быть определены и в плоскости любых других двух пере­менных, описывающих движение. Можно, например, рассматри­вать характеристики в плоскости переменных и, с. Для изэнтро-пического движения уравнения этих характеристик даются про-

v параллельных прямых (рис. 90).

сто равенствами /₊ = const, /_ = = const с произвольными по­стоянными в их правых частях (будем называть их условно ха­рактеристиками Г+ и Г_). Так, для политропного газа это есть согласно (104,3) два семейства

Замечательно, что эти харак­теристики всецело определяются

свойствами движущейся среды (газа) как таковой и не зави­сят от конкретного решения уравнений движения. Это связано с тем, что уравнение изэнтропического движения в переменных v, с есть (как мы увидим в следующем параграфе) линейное уравнение в частных производных второго порядка с коэффи­циентами, зависящими только от независимых переменных.

Характеристики в плоскостях х, t и и, с являются отобра­жениями друг друга с помощью заданного решения уравнений

') Для иллюстрации укажем пример такого случая: задача о движении газа при вдвигании или выдвигании поршня из бесконечной трубы. Здесь речь идет о нахождении решения газодинамических уравнений в области пло­скости х, t между двумя линиями: правой полуосью х и линией x = X(t), изображающей движение поршня (рис. 86, 87). На первой линии задаются значения двух величин (начальные условия v = 0, р — Ро при / = 0), а на второй — всего одной величины (о = и, где u(t) — скорость поршня).

движения. Это отображение, однако, отнюдь не должно быть взаимно однозначным. В частности, заданной простой волне со­ответствует всего одна характеристика в плоскости v, с, на ко­торую отображаются все характеристики плоскости х, t. Так, для волны, бегущей вправо, это есть одна из характеристик Г_; характеристики С_ отображаются на всю линию Г_, а характе­ристики С+—на отдельные ее точки.

§ 105. Произвольное одномерное движение сжимаемого газа

Рассмотрим теперь общую задачу о произвольном одномерг ном изэнтропическом движении сжимаемого газа (без ударных волн) и покажем прежде всего, что эта задача может быть све­дена к решению некоторого линейного дифференциального урав­нения.

Всякое одномерное движение (движение, зависящее всего от одной пространственной координаты) непременно потенциально, так как всякую функцию v (x,t) можно представить в виде про­изводной v(х, t) = д<р(х, t)/dx. Поэтому мы можем воспользо,-ваться в качестве первого интеграла уравнения Эйлера уравне­нием Бернулли (9,3):

ir + -_- ^{+ a,==0}-

С помощью этого равенства получаем для дифференциала d(p: d<V = ^dx + ^dt = vdx — (-у- + w) dt.

Независимыми переменными являются здесь х и t; произведем теперь переход к новым независимым переменным, выбрав в ка­честве таковых v и w. Для этого производим преобразование Лежандра; написав

dy = d(xv) — xdv — d[t + + td {w +-if) и введя вместо потенциала qp новую вспомогательную функцию X = Ф — *» + /(а» + 4")'

получаем:

dx = — х dv + td (а> + =tdw + (vt — x) dv,

где % рассматривается как функция от v и w. Сравнив это соот­ношение с равенством d% = -4^- dw -f- ^r^dv, имеем:

ИЛИ

_t==lL _x===vJtL_^L (105 П

dw ' dw dv v» /

Если функция %(v, w) известна, то по этим формулам опреде­лится зависимость к и к от координаты х и времени t.

Выведем теперь уравнение, определяющее %. Для этого исхо­дим из неиспользованного еще уравнения непрерывности

dp, д, _ч др. др. dv „

-|_Г+_Ж(Р«)=_Ж+^+Р_Ж-=0.

Преобразуем это уравнение к переменным v, ш. Написав частные производные в виде якобианов, имеем:

д(р, х) д (г, р) д (/, у) ___ _п

d(t, х) ¹ д (t, х) д (t, х)

или, умножая на d(t, х)/d(w, v):

д(р,х) д (/, р). a (t, v) q

<Э (а>, о) ' д (да, и) ~" 5 (да, о)

При раскрытии этих якобианов надо иметь в виду следующее. Согласно уравнению состояния газа плотность р есть функция каких-либо двух других независимых термодинамических вели­чин; например, можно рассматривать р как функцию от w и s. При s = const тогда будет просто р = р(ш); существенно при этом, что в переменных v, w плотность оказывается не завися­щей от v. Раскрывая якобианы, получаем поэтому

dp дх dp dt, dt ~

dw dv dw dv dw

Подставляя сюда для / и х выражения (105,1), получаем после сокращений:

р dw V dw dv² J '. dw¹ При s = const имеем dw = dp/р. Поэтому можно написать

dpdp dp p

dw dp dw c² '

Окончательно получаем для % следующее уравнение:

(скорость звука с надо рассматривать здесь как функцию от и>). Задача об интегрировании нелинейных уравнений движения приведена, таким образом, к решению линейного уравнения.

Применим полученное уравнение к политропному газу. Здесь с⁸ (у—\)w, и основное уравнение (105,2) принимает вид

Это уравнение может быть проинтегрировано в общем виде элв-
к 3-_Y

ментарным образом, если число _ | является целым четным числом:

7^Г = 2,г, Y = |r¥f- " = 0, 1, 2 (105,4)

Этому условию как раз удовлетворяют одноатомный (у = 5/3, и = 1) и двухатомный (у = 7/5, п = 2) газы. Вводя я вместо у, переписываем (105,3) в виде

Будем обозначать функцию, удовлетворяющую этому урав­нению при заданном я, посредством %_п- Для функции %₀ имеем|

^2w oV^ + ^T^⁰-

Введя вместо да переменную u — -y/2w, получаем:

д²Хо д²Хо ди² dv²

Но это есть обычное волновое уравнение, общее решение кото­рого есть: хо = Ы" + f)+ /г(и — у), где fi, /₂ — произвольные функции. Таким образом,

Xo = fi(V2a^-) + f_a(V2i»-o). (105,6)

Покажем теперь, что если известна функция %„, то функцию Хл+1 можно получить простым дифференцированием. В самом деле, дифференцируя уравнение (105,5) по ш, получаем после перегруппировки членов:

2 _£L (_дХ«Л, 2/г + З д (дхп \ _ (дхп\ _ _п

2п+\ ^w dw² \ dw J ^ 2п+\ dw \ dw) do² \ dw) ^U"

Если ввести вместо v переменную

, /2ге + 3

^v = ^с'V^+T¹

то получим для d%_n/dw уравнение

-- _-- _w JL (J2__\ + JL fJ____) -ЛГ-^) = о,

2 (re + 1) + 1 dw² \ dw) dw \ dw J dv'² \ dw J

совпадающее с уравнением (105,5) для функции %_n+i(w, v'). Та­ким образом, мы приходим к результату, что

Применяя эту формулу п раз к функции (Ю5,6), получаем искомое общее решение уравнения (105,5):

ЗС = (fi (л/2(2я+ 1)ш + v) + /2 (л/2(2я+ 1)ш - v)},

или

_%т- f FiW2{2n+l)w + v)+_F₂W2(2n+l)w-v)) _g,

dwⁿ~^l \ Уда У

где Fi, ^2 — снова две произвольные функции. Если ввести вместо до скорость звука согласно

с² 2п + 1 о

то решение (105,8) примет вид

Х-(тк)""{7М«+*ПП-) + 7'.(«--ЯТт)}- ^,,05'⁹» Выражения

о v — 1

стоящие в качестве аргумента в произвольных функциях, пред­ставляют собой не что иное, как инварианты Римана (104,3), постоянные на характеристиках.

В применениях часто возникает необходимость в вычислении значений функции %(v, с) на характеристике. Для этой цели слу­жит следующая формула¹):

f-E-Y-'j-L_/ff_e±—Е_^)\---------------------- -Ц- '<* + «>,(,05,10)

') Проще всего эту формулу можно вывести с помощью теории функций комплексного переменного, используя теорему Коши. Для произвольной функ­ции F{c -\- и) имеем: / д F(c + u) ^ V с дс) с _{= 2}-> f а Ч- + _{= 2}„-! <n-l)l * MV£+«)_ V дс² J с 2т j у₂ (z — с²)^п где интеграл берется в плоскости комплексного переменного z по контуру, охватывающему точку г = с^г. Положив теперь и «= с + а и произведя в ин­теграле подстановку -д/'г =2? — с, получим: !£ + ■.

1 («-DI £ ^ +

где теперь контур интегрирования по £ охватывает точку £ = с; снова при­меняя теорему Коши, находим, что этот интеграл совпадает с написанным в тексте выражением.

\cdcj \с V 2n+lJ) 2""¹ дс"-¹ с^{п v} '

при

с + а

(а — произвольная постоянная).

Д==-

Выясним теперь, в каком взаимоотношении с найденным здесь общим решением газодинамических уравнении находится решение, описывающее простую волну. Последнее отличается тем свойством, что в нем v и w являются определенной функцией друг от друга, v = v(w), и поэтому обращается тождественно в нуль якобиан

д (a, w)

д (х, t)

Между тем при преобразовании к переменным v, w нам при­шлось разделить уравнение движения на этот якобиан, в резуль­тате чего решение, для которого Д = 0, оказалось потерянным. Таким образом, простая волна не содержится непосредственно в общем интеграле уравнений движения, а является их особым интегралом.

Для понимания природы этого особого интеграла существен­но, однако, что он может быть получен из общего интеграла пу­тем своеобразного предельного перехода, тесно связанного с фи­зическим смыслом характеристик как линий распространения малых возмущений. Представим себе, что область плоскости v, w, в которой функция %(v, w) отлична от нуля, стягивается к очень узкой в (пределе — к бесконечно узкой) полосе вдоль одной из характеристик. Производные от х в поперечных к характери­стике направлениях пробегают при этом значения в очень широ­ком (в пределе — бесконечном) интервале, поскольку % очень быстро убывает в этих направлениях. Такого рода решения %(v,w) уравнений движения заведомо должны существовать. Действительно, рассматриваемые как «возмущение» в плоскости v, w они удовлетворяют условиям геометрической акустики и, как должно быть для таких возмущений, расположены вдоль характеристики.

Из сказанного ясно, что при такой функции у_и время t = = d%/dw будет пробегать сколь угодно большой интервал зна­чений. Производная же от % вдоль характеристики будет неко­торой конечной величиной. Но вдоль характеристики (например, одной из характеристик Г_) имеем:

dJ— j 1 dp dw j 1 dw q

dv pc dw dv с dv

Поэтому производная от % no v вдоль характеристики (обозна* чим ее как —f(v)) есть

d%_ __дг iJlLJlE. —4- ri2L__________________ f (_r,\

dv да ~ dw dv dv dw ^{1 yyh}

Выражая частные производные от х через х и t согласно (105,1), получим отсюда соотношение x = (v + c)t + f(v), т. е. как раз уравнение (101,5) простой волны. Соотношение же (101,4), уста­навливающее связь между у и с в простой волне, автоматически выполняется в силу постоянства /_ вдоль характеристики Г_

В § 104 было показано, что если в некоторой части плоскости х, t решение уравнений движения сводится к постоянному те­чению, то в граничащих с нею областях должна иметься простая волна. Поэтому движение, описывающееся общим решением (105,8), может следовать за постоянным движением (в частно­сти, за областью покоя), лишь через промежуточную стадию простой волны. Граница между простой волной и общим реше­нием, как и всякая граница между областями двух аналитически различных решений, есть характеристика. При решении различ­ных конкретных задач возникает необходимость в определении значения функции %(w,v) на этой граничной характеристике.

Условие сшивания простой волны с общим решением на гра­ничной характеристике получается подстановкой выражений (105,1) для х и t в уравнение простой волны x—(v±c)t-\-+ f(v); это дает

Дата добавления: 2014-11-07