Должно быть 6 страница

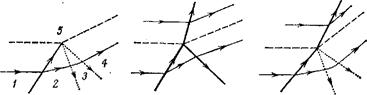
6)»)

• Ударная вша

---------------------- Тангещиапьный разрыв

...................... Слабый разрыв

---------------------- Линия тока

Рис. 102

В другом случае (рис. 102, в) возникают отраженная волна раз­режения и прошедшая в другую среду преломленная ударная волна. Обе эти конфигурации возможны только в определенных областях значений параметров падающей ударной волны и тан­генциального разрыва¹).

Взаимодействие двух тангенциальных разрывов может при­вести к конфигурации без приходящих»ударных волн, а лишь с двумя уходящими (что невозможно, как было указано выше, в отсутствии тангенциальных разрывов). В области / на рис. 103 газ покоится; конфигурация возможна, очевидно, лишь при сверхзвуковом течении в областях 2 и 5.

Остановимся кратко на пересечениях ударной волны с при­ходящим от постороннего источника слабым разрывом. Здесь могут представиться два случая в зависимости от того, является ли движение за ударной волной сверх- или дозвуковым. В пер­вом случае (рис. 104, а) слабый разрыв преломляется на удар­ной волне, проходя в пространство позади нее (сама же удар­ная волна в точке пересечения излома не имеет; ее форма имеет лишь особенность более высокого порядка —того же характера,

') Эти две конфигурации в известноу смысле обобщают случаи, изобра­женные на рис. 100 и 101,6.

что и особенность на слабом разрыве). Кроме того, изменение энтропии в ударной волне должно привести к возникновению позади нее еще и слабого тангенциального разрыва, на котором испытывают скачок производные энтропии.

Если же позади ударной волны течение становится дозвуко­вым, то слабый разрыв не может проникнуть в эту область и оканчивается в точке пересечения (рис. 104,6). Последняя яв­ляется в этом случае особой точкой (так, если падающий разрыв представляет собой раз­рыв первых производных гид­родинамических величин, ухо­дящий слабый тангенциальный разрыв, форма ударной волны и распределение давления в ок­рестности точки пересечения

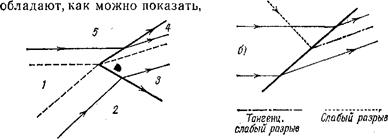
Рис. 103 Рис. 104

логарифмической особенностью). Кроме того, как и в предыду­щем случае, позади ударной волны возникает слабый тангенци­альный разрыв энтропии.')

Сказанное относительно взаимодействия ударных волн со слабым разрывом справедливо и для взаимодействия со сла­быми тангенциальными разрывами. Если течение в области за ударной волной сверхзвуковое, в ней возникают слабый и сла­бый тангенциальный разрывы. Если же течение за ударной вол­ной дозвуковое, то в нем возникает лишь преломленный слабый же тангенциальный разрыв.

Наконец, упомянем еще о взаимодействии слабых разрывов с тангенциальными. Если течение по обе стороны тангенциаль­ного разрыва сверхзвуковое, наряду с падающим возникают от­раженный и преломленный слабые разрывы. Если же течение по другую сторону тангенциального разрыва дозвуковое, сла­бый разрыв в него не проникает, происходит «полное внутрен­нее отражение» слабого разрыва.

') Детальное количественное исследование пересечений ударных волн со слабыми разрывами дано Дьяковым С. Л.— ЖЭТФ, 1957, т. 33, с. 948, 962.

§ 111. Пересечение ударных волн с твердой поверхностью

Фундаментальную роль в явлении стационарного пересече­ния ударных волн с поверхностью обтекаемого тела играет их взаимодействие с пограничным слоем. Свойства этого взаимо­действия весьма сложны и их детальное рассмотрение выходит за рамки этой книги. Мы ограничимся здесь лишь некоторыми общими утверждениями¹).

В ударной волне давление испытывает скачок, возрастая по направлению движения газа. Поэтому, если бы ударная волна пересекла поверхность тела, то вблизи места пересечения име­лось бы конечное возрастание давления на отрезке очень малой длины, т. е. имелся бы очень большой положительный градиент давления. Но мы знаем, что такое резкое возрастание давления вблизи твердой стенки невозможно (см. конец § 40); оно долж­но вызвать явление отрыва, в результате чего картина обтека­ния изменится таким образом, что ударная волна отодвинется на достаточное расстояние от поверхности тела. Исключение со­ставляют лишь ударные волны достаточно слабой интенсив­ности. Из изложенного в конце § 40 доказательства ясно, что невозможность положительного скачка давления на границе по­граничного слоя связана с предположением о достаточно боль­шой величине этого скачка: он должен превосходить некоторый предел, зависящий от значения R и убывающий с его увели­чением.

Таким образом, стационарное пересечение ударных волн с г > верхностью твердого тела возможно лишь для ударных волн не слишком большой интенсивности, — тем меньшей, чем выше R. Предельная допустимая интенсивность ударной волны зависит также и от того, является ли пограничный слой ламинарным или турбулентным. Турбулизация пограничного слоя затрудняет возникновение отрыва (§ 45). Поэтому при турбулентном погра­ничном слое от поверхности тела могут отходить более сильные ударные волны, чем при ламинарном пограничном слое.

Подчеркнем, что для изложенных рассуждений существенно, чтобы пограничный слой имелся перед ударной волной (т^ е. вверх по течению от нее). Поэтому сказанное выше не относится к волнам, отходящим от переднего края тела, как это может, например, иметь место при обтекании острого клина (о чем бу­дет подробно идти речь в следующем параграфе). В последнем случае газ подходит к краю угла извне, т. е. из пространства, в котором никакого пограничного слоя не существует; ясно поэтому, что изложенные соображения ни в какой мере не за-

') В пограничном слое непременно имеется прилегающая к поверхности тела дозвуковая часть, в которую ударная волна вообще не может проник­нуть. Говоря условно о пересечении, мы отвлекаемся от этого обстоятельства, несущественного для нижеследующих рассуждений.

трагивают возможности существования ударных волн, отходя­щих от края такого угла.

При дозвуковом движении отрыв может произойти лишь при возрастании давления в основном потоке вниз по течению вдоль обтекаемой поверхности. При сверхзвуковом же движении по­является своеобразная возможность возникновения отрыва и в области, где давление падает вниз по течению. Такое явление может осуществляться путем комбинирования ударной волны слабой интенсивности с отрывом, причем необходимое для воз­никновения отрыва повышение давления происходит в самой ударной волне; в области же перед ударной волной давление может при этом как возрастать, так и падать вниз по течению.

Все сказанное выше относится только к стационарному пере­сечению, при котором ударная волна и твердое тело покоятся друг относительно друга. Перейдем к рассмотрению нестацио­нарного пересечения, при котором на твердое тело падает при­ходящая извне движущаяся ударная волна, так что линия ее пе­ресечения с поверхностью тела передвигается вдоль последней. Такое пересечение сопровождается отражением ударной волны: наряду с падающей волной возникает еще одна, отраженная волна, отходящая от тела.

Будем рассматривать явление в системе координат, движу­щейся вместе с линией пересечения; в этой системе ударные

волны стационарны. Наиболее про-
стая картина отражения заключает-
ся в том, что отраженная волна от-
ходит непосредственно от линии пе-
ресечения; такое отражение назы-
w////^/^^ вается правильным (рис. 105). За-

данием угла падения oci и интенсив-
Рис- ¹⁰⁵ ности падающей волны однозначно
определяется движение в области 2.
В отраженной волне скорость газа должна повернуться на опре-
деленный угол так, чтобы снова стать параллельной поверхно-
сти тела. По этому углу положение и интенсивность отражен-
ной волны определяются уравнением ударной поляры. Но при
заданном угле поворота скорости ударная поляра определяет две
различные ударные волны: волны слабого и сильного семей-
ства (§ 92). Опытные данные показывают, что фактически от-
раженная волна всегда относится к слабому семейству, и ниже
будет подразумеваться именно этот выбор. Следует указать, что
при таком выборе при предельном переходе к бесконечно слабой
интенсивности падающей волны интенсивность отраженной вол-
ны тоже стремится к нулю, а угол отражения а₂ — к углу па-
дения ось как и должно было быть в соответствии с акустиче-
ским приближением. В пределе же aj->-0 отраженная волна
слабого семейства непрерывно переходит в волну, получаю-

щуюся для отражения при лобовом падении ударной волны (за­дача 1 § 100).

Математический расчет правильного отражения (в идеаль­ном газе) не представляет никаких принципиальных затрудне­ний, но алебраически весьма громоздок. Мы ограничимся здесь лишь изложением некоторых результатов¹).

07'

10'

60'

SO'

W

30'

Из общих свойств ударной поляры ясно, что правильное от­ражение возможно отнюдь не при произвольных значениях пара­метров падающей волны (угла падения ai и отноше­ния рг/Pi)• При заданном значении p₂/pi существует предельный допустимый угол он*; при ai ~> а,\и правиль­ное отражение невозможно. При р₂/р\ ~* 1 предельный угол стремится к 90°, т. е. правильное отражение воз-

Рис. 107

можно при всяком угле падения. В пределе же p₂/pi-*-oo он

стремится к некоторому значению, зависящему от у; для воздуха

это 40°. На рис. 106 дан график ai* как функции р\/р₂ для

Y =* 7/5 и у = 5/3.

Угол отражения <х₂, вообще говоря, не совпадает с углом

падения. Существует определенное значение а» угла падения,

такое, что'при ai < а* угол отражения а₂ < щ; если же

ai > а», то а₂> а\. Значение а, есть

1 у — 1

а, = — arc cos

(для воздуха а* = 39,2°); замечательно, что оно не зависит от интенсивности падающей волны.

') Более подробное изложение вопроса об отражении ударных волн мож­но найти в книгах: Курант Р., Фридрихе К. Сверхзвуковое течение и ударные волны. — М.: ИЛ, 1950, гл. IV [Courant R., Friedrichs К- Supersonic flow and shock waves. — N. Y.: Interscience, 1948]; Мизес P. Математическая теория течения сжимаемой жидкости. М.: ИЛ, 1961, § 23 [Mises R. Mathematical theory of compressible fluid flow. — N. Y., Academic Press, 1958], а также в обзорной статье: Bleakneu W., Taub A. H. — Rev. Mod. Physics, 1949, v. 21. _P. 584.

При си > aik правильное отражение невозможно и падаю­щая ударная волна должна разветвиться на некотором расстоя­нии от поверхности тела, так что возникает картина изображен­ного на рис. 107 типа с тройной конфигурацией ударных волн и отходящим от точки разветвления тангенциальным разрывом (такую конфигурацию называют маховским отражением).

§ 112. Сверхзвуковое обтекание угла

При исследовании движения вблизи края угла на поверх­ности обтекаемого тела снова достаточно рассматривать лишь небольшие участки вдоль края угла и потому можно считать этот край прямым, а самый угол образованным двумя пересе-

q кающимися плоскостями.

Мы будем говорить об обте­кании выпуклого угла, если

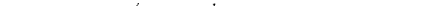течение происходит в угле,, большем чем я, и об обте­кании вогнутого угла, если газ движется внутри угла, меньшего чем я.

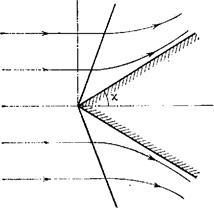
Дозвуковое обтекание угла по своему характеру ни­чем не отличается от обтека­ния несжимаемой жид­костью. Сверхзвуковое же обтекание обладает совер­шенно иным характером; су­щественной его особен­ностью является возникнове­ние отходящих от края угла разрывов.

Рассмотрим сначала воз­можные режимы обтекания, когда сверхзвуковой поток газа подходит к краю угла, двигаясь вдоль одной из его

вдоль другой стороны угла. Обратим внимание на то, что при та­ком обтекании не образуется никаких турбулентных областей; при аналогичном же обтекании несжимаемой жидкостью непре­менно возникает турбулентная область с линией отрыва по краю угла (рис. 24).

Пусть V\ — скорость натекающего потока (У на рис. 108)',
а С\ — скорость звука в нем. Положение слабого разрыва Оа
определяется непосредственно по числу Mi = vi/ci условием,
чтобы он пересекал линии тока под углом, равным углу Маха.
Изменение скорости и давления в волне разрежения опреде-
ляется формулами (109,12—15), причем надо только установить
направление, от которого должен производиться отсчет угла ср
в этих формулах. Прямому лучу tp = 0 соответствует v = с == с»;
при Mi > 1 такой линии фактически нет, так как везде v/c > 1.
Представляя себе, однако, волну разрежения формально про-
дленной в область левее Оа и воспользовавшись формулой
(109,12), найдем, что разрыву Оа надо приписать значение
угла ср, равное ______

Рис. 110

и затем увеличивать ср в направлении от Оа к Ob. Положение разрыва Ob определяется моментом, когда направление ско­рости станет параллельным стороне угла ОВ.

Рис. 109

Угол поворота течения в волне разрежения не может превы­шать значение хтах, вычисленное в задаче 2 § 109. Если вели­чина обтекаемого угла 8 < я — Хтах, то волна разрежения не может повернуть поток на требуемый угол и возникает картина, изображенная на рис. 108,6. Разрежение в волне 2 происходит тогда вплоть до равного нулю давления (достигаемого на ли­нии Об), так что волна разрежения отделена от стенки об­ластью вакуума 3.

Описанный режим обтекания, однако, не является единствен­но возможным. На рис. 109 и 110 изображены режимы, при ко­торых ко второй стороне угла прилегает область неподвижного газа, отделенная от движущегося тангенциальным разрывом; как всегда, тангенциальный разрыв размывается в турбулент­ную область, так что этот случай соответствует наличию от­рыва¹). Поворот течения на некоторый угол происходит в волне разрежения (рис. 109) или в ударной волне (рис. ПО). Послед­ний случай, однако, возможен лишь при не слишком большой интенсивности ударной волны (согласно общим соображениям, изложенным в предыдущем параграфе).

Какой из описанных режимов осуществляется в том или ином конкретном случае, зависит, вообще говоря, от условий те­чения вдали от края угла. Так, при вытекании газа из сопла (краем угла является при этом край отверстия сопла) суще­ственно взаимоотношение между выходным давлением газа р_х и давлением во внешней среде р_е. Если р_г < pi, то обтекание происходит по типу рис. 109; положение и угол раствора волны разрежения определяются при этом условием, чтобы давление в областях 3—4 совпадало с р_е; чем меньше р_е, тем на больший угол должно повернуться течение. Однако.если обтекаемый угол В на рис. 109 слишком велик, то давление газа может не успеть дойти до требуемого значения р_е — направление скорости станет параллельным стороне ОВ угла раньше, чем давление упадет до этого значения. Движение вблизи края сопла будет тогда про­исходить по типу рис. 107. Давление вблизи внешней стороны ОВ отверстия целиком определяется при этом углом 8 и не за­висит от значения р_е; окончательное же падение давления до р_е произойдет лишь на некотором расстоянии от отверстия.

Если же р_е > рь то обтекание края отверстия сопла проис­ходит по типу рис. ПО с образованием отходящей от края от­верстия ударной волны, повышающей давление от р\ до р_е. Это возможно, однако, лишь при не слишком больших превышениях р_е над р\, когда интенсивность ударной волны не слишком ве­лика; в противном сучае отрыв возникает на внутренней поверх­ности сопла и ударная волна перемещается вместе с ним внутрь сопла, о чем уже шла речь в § 97.

Далее, рассмотрим обтекание вогнутого угла. В дозвуковом случае такое обтекание сопровождается возникновением отрыва на некотором расстоянии, не доходя до края угла (см. коней § 40). При натекании же сверхзвукового потока изменение его направления может осуществиться в отходящей от края угла ударной волне (рис. 111). Здесь снова необходимо оговорить, что фактически такой простой безотрывный режим возможен лишь при не слишком сильной ударной волне. Интенсивность ударной

') Согласно экспериментальным данным сжимаемость глаза несколько уменьшает угол раствора турбулентной области, в которую размывается тан­генциальный разрыв.

волны возрастает по мере увеличения угла х осуществляемого ею поворота течения; поэтому можно сказать, что безотрывное обтекание возможно лишь при не слишком больших значениях %.

Обратимся теперь к картине движения, возникающей, когда
на край угла натекает свободный сверхзвуковой поток (рис. 112).
Поворот течения в направление, параллельное сторонам угла,
происходит в отходящих от края угла ударных волнах. Как уже
было объяснено в предыду-
щем параграфе, это есть как #|
раз тот исключительный слу-
чай, когда от поверхности
твердого тела может отхо-
дить ударная волна произ-
вольной интенсивности.

Зная скорости Vi и С\ в натекающем потоке /, можно

W77777777777-

Рис. 111

определить положение ударных волн и движение газа в обла­стях, расположенных за ними. Направление скорости v₂ должно быть параллельно стороне ОВ угла:

V₂y/v₂x = tg Х-

Поэтому определение v₂ и угла ф ударной волны производится непосредственно по диаграмме ударной поляры с помощью луча, прс веденного из начала координат под заданным углом х к оси абсцисс (см. рис. 64), как это было подробно объяснено в § 92. Мы видели, что при заданном угле % ударная поляра опреде­ляет две различные ударные волны" с различными углами ф. Одна из них (соответствующая точке В на рис. 64), более сла­бая, оставляет течение, вообще говоря, сверхзвуковым; другая же, более сильная, превращает его в дозвуковое. В данном слу­чае для обтекания углов на поверхности конечных тел следует всегда выбирать первую из них, волну «слабого» семейства. Не­обходимо иметь в виду, что в действительности этот выбор опре­деляется условиями обтекания вдали от угла. При обтекании очень острого угла (малое х) образующаяся ударная волна должна, очевидно, обладать очень малой интенсивностью. Есте­ственно считать, что по мере увеличения этого угла интенсив­ность волны будет расти монотонно; этому соответствует как раз перемещение по участку QC кривой ударной поляры (рис. 64) от точки Q к точке С¹).

Мы видели также в § 92, что угол поворота вектора скорости в ударной волне не может превосходить некоторого определен­ного (зависящего от Mi) значения хтах. Поэтому описанная кар­тина обтекания невозможна,.если какая-либо из сторон обтекае­мого угла наклонена к направлению натекающего потока под углом, превышающим %_тах (в таком случае движение газа в области вблизи угла должно быть дозвуковым, что фактически

осуществляется путем возникнове­ния ударной волны где-либо впереди тела; см. § 122). Поскольку %_тах— монотонно возрастающая функция М_ь то можно также сказать, что при заданном значении угла % чис­ло Mi натекающего потока должно превышать определенное значение

Mi mi„.

Наконец, укажем, что если сто­роны угла расположены по отноше­нию к натекающему потоку как по­казано на рис. 113, то ударная волна возникает, разумеется, лишь по одну сторону угла; поворот же потока по другую сторону осуществляется в волне разрежения.

Задачи

1. Определить положение и интенсивность ударной волны при обтекании очень малого угла (х "С 1) при не слишком больших значениях числа Маха: Mix < 1.

Решение. При % <. 1 ударная поляра определяет два значения: близ­кое к я/2 (близость к точке Р на рис. 64) и близкое к углу Маха ai (бли­зость к точке Q). Интересующей нас волне слабого семейства отвечает вторая из них. Из (92,11) имеем при % < 1:

М, sin" ф — 1

У+ 1

Mftgai

М

V^м!-

Подставив это выражение в (92,9), найдем:

р₂ - р, уМ²

Pl

V^м!-¹

') Ср., однако, примечание на стр. 594. Что касается формального во­проса об обтекании клина, образованного двумя бесконечными плоскостями, ТО он не представляет физического интереса.

Угол ф ищем в виде ф = ai -f- е, sCai и из того же выражения «аходим

Y + 1 М^г

ф - ai = ' х-

4 М, — 1

При Mi > 1 угол ai «1/Mi и для справедливости полученных формул долж­но быть xMi < 1.

2. То же если число Mi настолько велико, чго Mix >■ I.

Решение. В этом случае углы ф и % одинакового порядка малости. Из (92,11) находим

Y+ 1 Ф--2-Х-

Для отношения давлений имеем согласно (92.9)

Значение М₂ позади волны (из 92,12)):

X V Y(Y-

l)'

•Т.е. остается большим по сравнению с 1, но не по сравнению с 1/х- В том же приближении

р2 _ Y + 1 1г _{= (}

Pi Y — 1 '»i

(разность уi — Х1г ~ fiX²)- Поэтому уменьшение числа Маха фактически свя­зано лишь с увеличением скорости звука: M₂/Mi = C\jc%.

§ 113. Обтекание конического острия

Исследование сверхзвукового стационарного течения вблизи острия на поверхности обтекаемого тела представляет собой трехмерную задачу, и потому несравненно сложнее исследова­ния обтекания угла с линейным краем. Полностью может быть решена задача об осесимметричном обтекании острия, которое мы здесь и рассмотрим.

Вблизи своего конца осесимметрическое острие можно рас­сматривать как прямой конус кругового сечения, и таким обра­зом, задача состоит в исследовании обтекания конуса однород­ным потоком, натекающим в направлении оси конуса. С каче­ственной стороны картина выглядит следующим образом.

Как и при аналогичном обтекании плоского угла, должна воз­никнуть ударная волна (Л. Busemann, 1929); из соображений симметрии очевидно, что эта волна будет представлять собой коническую поверхность, коаксиальную с обтекаемым конусом и имеющую общую с ним вершину (на рис. 114 изображен раз­рез конуса плоскостью, проходящей через его ооь). Однако в отличие от плоского случая ударная волна не осуществляет здесь поворота скорости газа на полный угол х. необходимый для те­чения вдоль поверхности конуса (2%—угол раствора конуса). После перехода через поверхность разрыва линии тока искрив­ляются, асимптотически приближаясь к образующим обтекае­мого конуса. Это искривление сопровождается непрерывным уплотнением (добавочным к уплотнению в самой волне) и соот­ветственным падением скорости.

Изменение направления и величины скорости на самой удар-
ной волне определяется ударной полярой, причем и здесь осу-
ществляется решение, отве-
чающее «слабой» ветви по-
ляры¹). Соответственно, для
каждого значения числа Ма-
ха натекающего потока
Mi=t>i/ci существует опре-
деленное предельное значе-
ние угла полураствора ко-
нуса хтах, за которым такое
обтекание становится невоз-
можным и ударная волна
«отсоединяется» от вершины
конуса. Поскольку за удар-
ной волной происходит до-
полнительный поворот тече-
ния, значения хтах для обте-
кания конуса превышают
Рис. 114 (при одинаковых Mi) значе-

ния Хтах ДЛЯ ПЛОСКОГО СЛу-

чая (обтекания клина). Непосредственно за ударной волной дви­жение газа обычно сверхзвуковое, но может быть и дозвуковым (при х, близких к Хтах). Сверхзвуковое за ударной волной тече­ние по мере приближения к поверхности конуса может стать дозвуковым, и тогда на определенной конической поверхности скорость проходит через звуковое значение.

Коническая ударная волна пересекает все линии тока нате­кающего потока под одинаковым углом, а потому обладает по­стоянной интенсивностью. Отсюда следует (см. ниже § 114), что и за ударной волной течение будет изэнтропическим и по­тенциальным.

В силу симметрии задачи и ее автомодельности (отсутствия в ее условиях какой-либо характеристической постоянной длины) очевидно, что распределение всех величин (скорости, давления) в потоке за ударной волной будет функцией только от угла 6 на­клона к оси конуса (оси х на рис. 114) радиус-вектора, прове-

') Это может, однако, быть не так при некоторых «экзотических» формах обтекаемого тела Так, существуют указания на отбор волны «сильного» се­мейства при обтекании конуса на переднем крае широкого тупого тела.

денного в данную точку из вершины конуса. Соответственно уравнения движения сводятся к обыкновенным дифференциаль­ным уравнениям; граничные условия к этим уравнениям на удар­ной волне определяются уравнением ударной поляры, а на по­верхности конуса — требуют параллельности скорости образую­щим конуса. Эти уравнения, однако, не могут быть проинтегри­рованы в аналитическом виде и должны решаться численным образом. Отсылая за результатами таких вычислений к ориги­нальным источникам¹), мы ограничимся лишь кривой (рис. 65), дающей зависимость предельного допустимого угла раствора конуса 2хтах как функции от числа Mi. Укажем также, что при Mi —»-1 угол /шах стремится к нулю по закону

Хтах = COnst Д/~^р, (113,1)

как это можно заключить на основании общего околозвукового закона подобия (126,11) (const есть число, не зависящее ни от М_ь ни от рода газа).

Замкнутое аналитическое решение задачи об обтекании ко­нуса возможно лишь в предельном случае малых углов раствора конуса (Г/г. Кагтап, N. В. Moor, 1932). Очевидно, что в таком случае скорость газа во всем пространстве будет лишь незначи­тельно отличаться от скорости vi натекающего потока. Обозна­чив посредством v малую разность между скоростью газа в дан­ной точке и скоростью Vi и введя ее потенциал ср, мы можем применить для последнего линеаризованное уравнение (114,4); если ввести цилиндрические координаты х, г, со с осью вдоль оси конуса (со — полярный угол), это уравнение примет вид

Ш'3г)+-Г&-Г&-Ь «13.2,

или для осесимметрического движения

-*>^г0=°. сад

где введено обозначение

6 = (М²-1)¹/². (113,4)

Для того чтобы распределение скорости было функцией только от угла 9, потенциал должен иметь вид ср =xf{%), где g = г/х = = tg 6. Сделав подстановку, получим для функции /(g) урав­нение

*) См. Taylor G. /., Maccol J. W. — Proc. Roy. Soc, 1933, v. 139A, p. 278; Maccol J. W. — Proc. Roy. Soc, 1937, v. 159A. p. 459. См. также изложение в книге: Кошн Н. Е.. Кибгль И. А., Роне Н. В. Теоретическая гидромехани­ка. — М.: Физматгиз, 1963, ч. II, § 27.

Е(1-Э"&²)Г+Г = 0.

которое решается элементарно. Тривиальное решение / = const соответствует однородному потоку, а второе решение есть

/ = const (Vl - $%² - Arch ~).

Граничное условие на поверхности конуса (т. е. при | = tg % «%} гласит:

или f' — Vi%. Отсюда const. = Vix², и в результате получим сле­дующее окончательное выражение для потенциала (в области

*>рг>)):

Ф = *>if [V*² - Р^² - х Arch jp]. (113,6)

Обратим внимание на то, что ф имеет при г—>-0 логарифмиче­скую особенность.

Отсюда находим компоненты скорости:

^ = -f,X² Arch^, _Ur==i^lV^²-pV². (П3,7>

Давление на поверхности конуса вычисляется с помощью фор­мулы (114,5); благодаря логарифмической особенности ф при г->-0 скорость v, на самой поверхности конуса (т. е. при ма­лых г) велика по сравнению с v_x, и потому в формуле для дав­ления должен быть сохранён член с v_r. В результате получим:

p-p₁ = p₁t-2_X²(ln^_r-|). (113,8)

Все эти формулы, полученные с помощью линеаризованной тео­рии, теряют применимость при слишком больших значениях М_ь сравнимых с 1/х (см. § 127).

Дата добавления: 2014-11-07