Должно быть 11 страница

Распределение давления получается по формуле

(в общей формуле (114,5) членом с v² можно в данном случае пренебречь, так как v_x и v_y — одинакового порядка величины). Подставив сюда (125,3) и вводя так называемый коэффициент давления С_р, получим в верхней полуплоскости

В частности, коэффициент давления, действующего на верхнюю поверхность крыла, есть

С_р2 = }&(*). (125,4)

Аналогично найдем для нижней поверхности

C_pl = -jZ,\(x). (125,5)

Отметим, что давление в каждой точке профиля сечения крыла оказывается зависящим только от наклона его контура в этой же точке.

Поскольку угол наклона линии контура профиля к оси к везде мал, то вертикальная проекция сил давления равна с до­статочной точностью самому давлению. Результирующая дей­ствующая на крыло подъемная сила равна разности сил давле­ния, действующих на ее нижнюю и верхнюю поверхности. По­этому коэффициент подъемной силы

(определение длин l_x, 1_У см. рис. 129, а). Определим угол атаки а как угол наклона к оси х хорды АВ, проведенной через вершины острых кромок (рис. 129,а): ал:1_у/1_х; тогда получим оконча­тельно простую формулу:

C_v= -gL- (125,6)

V^м?-¹

(/. Ackeret, 1925). Мы видим, что подъемная сила определяется одним только углом атаки и не зависит от формы сечения кры­

С_х

4a²+2(e'f + 9²)

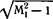
(125,8)

(черта обозначает усреднение по х). При заданном угле атаки коэффициент сопротивления, очевидно, минимален для крыла, представляющего собой плоскую пластинку (так что 0_t = 0₂ = = 0). В этом случае С_х = аС_у. Если применить формулу (125,8) к шероховатой поверхности, то мы найдем, что шероховатость может привести к значительному увеличению сопротивления, даже если высота отдельных неровностей мала ^.Действительно, сопротивление оказывается не зависящим от высоты отдельных неровностей, если не меняется средний наклон их поверхности, т.е. среднее отношение высоты неровностей к расстоянию между ними.

Наконец, сделаем еще следующее замечание. Здесь, как и везде, говоря о крыле, мы подразумеваем, что оно расположено своими кромками перпендикулярно к движению. Обобщение на случай любого угла у между направлением движения и кромкой (угол скольжения) вполне очевидно. Ясно, что силы, действую­щие на бесконечное крыло постоянного сечения, зависят только от нормальной к его кромкам составляющей скорости натекаю­щего потока; в невязкой жидкости составляющая скорости, па­раллельная кромкам, не вызывает никаких сил. Поэтому силы, действующие на крыло со скольжением в потоке с числом Mi,— такие же, какие действовали бы на то же крыло без скольжения в потоке с числом Mi, равным Mi sin у. В частности, если Mi > 1, но Mi sin у < 1, то специфическое для сверхзвукового обтекания волновое сопротивление будет отсутствовать.

') Но все же больше толщины пограничного слоя.

§ 126. Околозвуковой закон подобия

Развитая в §§ 123—125 теория сверх- и дозвуковых обтека­ний тонких тел неприменима в случае околозвукового движения, когда становится несправедливым линеаризованное уравнение для потенциала. В этом случае картина течения во всем про­странстве определяется нелинейным уравнением (114,10):

*-£-&—£-+-& <¹²⁶.'>

(или, при плоском движении, эквивалентным ему уравнением Эйлера —- Трикоми). Решение этих уравнений для конкретных случаев, однако, весьма затруднительно. Поэтому существенный интерес представляют правила подобия, которые можно устано­вить для таких течений, не прибегая к их конкретному решению. Рассмотрим сначала плоское течение, и пусть

Y = 6f(x/l) (126,2)

есть уравнение, определяющее форму обтекаемого тонкого кон­тура, причем / есть его длина (в направлении обтекания), а 6 характеризует его толщину (6<С/). Изменением двух парамет­ров I и 6 получим семейство подобных контуров. Уравнение движения гласит:

со следующими граничными условиями. На бесконечности ско­рость равна скорости vi невозмущенного потока, т. е.

(см. определение потенциала ф согласно (114,9)). На профиле же скорость должна быть направлена по касательной к нему:

в„ (Эф dY б /х\

ввиду тонкости профиля можно требовать выполнения этого условия при у = 0.

Введем новые безразмерные переменные согласно

l - Ш^2/3 _

х = 1х, у = ^ у₁₃у, Ф = —1/гф(*. 9) (126,6)

(мы ввели угол 0 = 6//, характеризующий «угол раствора» тела или угол атаки). Тогда мы получим уравнение

„ дф <Э²ф д²ф

с граничными условиями

f=0н.оо, f при 8^0.

K = Thas- (126,7)

где

М, — 1 (о.в)^:

Эти условия содержат лишь один параметр: К. Таким образом, мы получили искомый закон подобия: плоские околозвуковые те­чения с одинаковыми значениями числа К подобны, как это уста­навливается формулами (126,6) (С. В. Фалькович, 1947).

Обратим внимание на то, что в выражение (126,7) входит также и единственный параметр а*, характеризующий свойства самого газа. Поэтому полученное правило определяет также и подобие по изменению рода газа.

В условиях рассматриваемого приближения давление опре­деляется формулой

Вычисление с помощью выражений (126,6) показывает, что коэффициент давления на профиль будет функцией вида

£'(*• тУ

Коэффициенты силы сопротивления и подъемной силы опреде­ляются интегралами по контуру профиля:

C_x = -j\c_p^dx, C_y=j§C_pdx

и, следовательно, являются функциями вида ')

fl5/3 _fl2/3

С_х = ±щ-Ш). С_у = ±щГ_у{К). (126,8)

Совершенно аналогичным образом можно получить закон подобия для трехмерного обтекания тонкого тела, форма кото­рого задается уравнениями вида

У = 6/, (у), Z = 6f₂(-f) (126,9)

с двумя параметрами б и /(б <С /). Существенное отличие от плоского случая связано с тем, что потенциал имеет при

') Область применимости этих формул определяется неравенством | Mi — 1| < 1. Линеаризованной же теории соответствуют большие значе­ния К, т. е. | Mi — 11» в²". В области 1 > Mi — 1 > б²/' формулы (126,8) должны, следовательно, переходить в формулы (125,6—8) линеаризованной теории. Это значит, что при больших К функции f_x и /„ должны быть про­порциональны К~^иг.

2->-0 логарифмическую особенность (см., например, формулы обтекания тонкого конуса в § 113). Поэтому граничное условие на оси х должно определять не сами производные дщ/ду, dcp/dz, а остающиеся конечными произведения:

" ду dx ' дг dx '

Легко убедиться в том, что преобразованием подобия в этом случае является (снова вводим угол 0 = 6/£)

x = lx, y = —L^g, z = —i—г, ф = /е²ф, (126,10)
оа. На,

причем параметр подобия

(126,11)

(Т. Кагтап, 1947). Для коэффициента давления на поверхность тела получим выражение вида

С_Р = &Р(К, х/1),

а для коэффициента силы сопротивления соответственно')

С_л = 6⁴/(/С). (126,12)

Все полученные формулы относятся, конечно, как к малым положительным, так и к малым отрицательным значениям Mi—1. Если в точности Mi = 1, то параметр подобия /(= 0 и функции в формулах (126,8) и (126,12) сводятся к постоянным, так что эти формулы полностью определяют зависимость С_х и С_у от угла 6 и свойств газа а[11].

§ 127. Гиперзвуковой закон подобия

Для обтекания тонких заостренных тел с большими сверх­звуковыми скоростями (большие М^ линеаризованная теория неприменима, как это уже было упомянуто в конце § 114. По­этому представляет особый интерес простое правило подобия, которое можно установить для таких течений (их называют ги­перзвуковыми).

Возникающие при таком обтекании ударные волны накло­нены к направлению движения под малым углом — порядка ве­личины отношения 0 = 6// толщины тела к его длине. Эти вол­ны, вообще говоря, искривлены и в то же время обладают боль­шой интенсивностью — хотя скачок скорости на них относительно мал, но скачок давления (а с ним и энтропии) велик. Поэтому течение газа в общем случае отнюдь не является потенциальным.

') В области 1» Mi — 1 3> 9² должна получаться формула (123,7) ли­неаризованной теории, согласно которой С_х ~ 9⁴; это значит, что при увели­чении К функция f(K) должна стремиться к постоянной.

Будем считать, что число Mi — порядка величины 1/0 или больше. Ударная волна понижает значение местного числа М, но оно во всяком случае остается порядка величины 1/0 (ср. за­дачу 2 § 112), так что число М велико во всем пространстве.

Воспользуемся указанной в § 123 «звуковой аналогией»: трёхмерная задача о стационарном обтекании тонкого тела с переменным сечением S(x) эквивалентна нестационарной двух­мерной задаче об излучении звуковых волн контуром, площадь которого меняется со временем по закону S(vit); роль скорости звука играет при этом величина t>i (МТ — 1)~^1/2 или при боль­ших Mi просто С\. Подчеркнем, что единственное условие, обес­печивающее эквивалентность обеих задач, заключается в ма­лости отношения 6//, что дает. возможность рассматривать не­большие вдоль длины тела кольцевые участки его поверхности как цилиндрические. При больших М_ь однако, скорость распро­странения излучаемых волн сравнима по величине со скоростью частиц газа в них (ср. конец § 123), и потому задача должна решаться на основе точных, нелинеаризованных уравнений.

Возмущение скорости (по сравнению со скоростью vi нате­кающего потока) мало уже при всяком сверхзвуковом обтекании тонкого заостренного тела. При гиперзвуковом обтекании допол­нительно еще возмущение продольной скорости мало по срав­нению с возникающими поперечными скоростями:

v_y ~ v_z ~ i>)0, v_x —• с, ~ Oi©². (127,1)

Изменения же давления и плотности отнюдь не малы:

J^Pl-~M²0², IlUlL^i, ₍₁₂₇,2)

Pi Pi '

причем изменение давления может быть даже (при М]0 > 1) сколь угодно большим (ср. задачу 2 § 112).

Звуковая аналогия относится, очевидно, только к двухмер­ной задаче о движении в плоскости у, г, перпендикулярной направлению натекающего потока. В этой двухмерной задаче линейная скорость источника звука — порядка величины»i0; кроме нее в задачу входят в качестве независимых параметров еще только скорость звука с\ и размеры источника б (и пара­метр плотности pi)¹). Из них можно составить всего одну без­размерную комбинацию

/C = MiQ, (127,3)

которая и является критерием подобия^[12]). В качестве масшта­бов длины для координат у, z и масштаба времени надо при этом взять величины соответствующей размерности, составлен­ные из тех же параметров, например, б и 5/t>i9 = l/v\\ естествен­ным же параметром для координаты х является длина тела /. Тогда можно утверждать, что

v_y = vfiv'_y, v_z = vfiv'_z, p = _Plvpy, р = р,р', (127,4)

где v, %)'_z, р', р' — функции безразмерных переменных х/1,

у/8, г/б и параметра К; при этом в виду (127, 1—2) можно утверждать, что эти функции — порядка единицы^[13]). Сила сопротивления F_x вычисляется как интеграл

F_x = <§> Р dy dz,

взятый по всей поверхности тела (в силу граничного условия у„ = 0, член v_x(vn) в плотности потока импульса обращается в нуль на поверхности тела; п — нормаль к. этой поверхности). Перейдя к безразмерным переменным согласно (127,4), получим коэффициент сопротивления С_х (определенный согласно (123,6)) в виде

С_х = 29^[14] ф р' dy' dz'.

Оставшийся интеграл — функция безразмерного параметра К. Таким образом,

С, = в^[15]/(Ю- (127,5)

Такой же самый закон подобия получается, очевидно, и в плоском случае — для обтекания тонкого крыла бесконечной про­тяженности. Для коэффициентов сопротивления и подъемной силы получаются при этом формулы вида

С_Х=&ЫЮ, C_y = &f_e(K). (127,6)

страненной на нелинейную задачу, указана Хейзом (W. D. Hayes, 1947);

При применении законов (127,5—6) следует помнить, что по­добие течений предполагает, что форма, размеры и ориентация обтекаемых тел относительно натекающего потока получаются друг из друга только изменением масштаба б вдоль осей у, г и масштаба / вдоль оси х. Это значит, в частности, что если от­личен от нуля угол атаки а, то для подобных конфигураций отношение а/0 должно быть одинаковым.

При Ki->oo функции этого параметра в (127,5—6) стре­мятся к постоянным пределам. Это утверждение является след­ствием существования предельного (при Mi-»-oo) режима обте­кания, свойства которого в существенной области течения не зависят от Mi (С. В. Валландер, 1947; К- Oswatitsch, 1951). Под «существенной» подразумевается область течения между перед­ней, наиболее интенсивной, частью головной ударной волны и поверхностью обтекаемого тела, не слишком далеко от его пе­редней части (подчеркнем, что именно эта область, с наиболь­шим давлением, определяет действующие на тело силы). Если описывать течение «приведенными» скоростью v/v\, давлением р1р{о'\ и плотностью p/pi как функциями безразмерных коорди­нат, то картина обтекания тела заданной формы в указан­ной области оказывается в пределе независящей от Mi. Дело в том, что, будучи выраженными через эти переменные, оказы­ваются независящими от Mi не только гидродинамические урав­нения и граничные условия на поверхности обтекаемого тела, но и все условия на поверхности ударной волны. Ограничение области движения «существенной» частью связано с тем, что пренебрегаемые в последних условиях величины — относитель­ного порядка l/М² sin²q>, где q> — угол между vi и поверхностью

разрыва; на больших расстояниях, где интенсивность ударной волны мала, этот угол стремится к углу Маха arcsin(l/Mi)«1/М], так что параметр разложения пере­стает быть малым: 1/М² sin²<p ~ ~ 1 ').

Задача

Определить подъемную силу, дей-
ствующую на плоское крыло бесконеч-
р_ис 1зо ного размаха, наклоненное к направ-

лению движения под малым углом атаки а при Mia^Sl (R. D. Linnell, 1949). Решение. Картина обтекания выглядит, как показано на рис. 130: от переднего и от заднего краев пластинки отходят по ударной волне и по волне разрежения, в которых поток поворачивает сначала на угол а, а затем на такой же угол в обратном направлении.

Согласно акустической аналогии задача о стационарном обтекании такой пластинки эквивалентна задаче о нестационарном одномерном движении газа впереди и позади поршня, движущегося равномерно со скоростью av_t. Впере­ди поршня образуется ударная волна, а позади — волна разрежения (см. за­дачи 1, 2 § 99). Воспользовавшись полученными там результатами, находим искомую подъемную силу как разность давлений, действующих на обе сто­роны пластинки. Коэффициент подъемной силы:

(где К = aMi). При /(5» 2/ (у — 1) под пластинкой образуется область ва­куума и второй член должен быть опущен. В области 1 < Mi < 1/а эта формула переходит в формулу C_t — 4a/Mi, даваемую линеаризованной тео­рией, в соответствии с тем, что здесь перекрываются области применимости той и другой.

ГЛАВА XIV

ГИДРОДИНАМИКА ГОРЕНИЯ

§ 128. Медленное горение

Скорость химической реакции (измеряемая, скажем, числом прореагировавших в единицу времени молекул) зависит от тем­пературы газовой смеси, в которой она происходит, увеличиваясь вместе с ней. Во многих случаях эта зависимость очень силь­ная^[16]). Скорость реакции может при этом оказаться при обыч­ных температурах настолько малой, что реакция практически вовсе не идет, несмотря на то, что состоянию термодинамиче­ского (химического) равновесия соответствовала бы газовая смесь, компоненты которой прореагировали друг с другом. При достаточном же повышении температуры реакция протекает со значительной скоростью. Если реакция эндотермична, то для ее протекания необходим непрерывный подвод тепла извне; если ограничиться одним только начальным повышением температуры смеси, то прореагирует лишь незначительное количество веще­ства, вслед за чем температура газа настолько понизится, что реакция снова прекратится. Совсем иначе будет обстоять дело при сильно экзотермической реакции, сопровождающейся значи­тельным выделением тепла. Здесь достаточно повысить темпе­ратуру хотя бы в одном каком-нибудь месте смеси; начавшаяся в этом месте реакция в результате выделения тепла сама будет производить нагревание окружающего газа и, таким образом, реакция, раз начавшись, будет сама собой распространяться по газу. В таких случаях говорят о медленном горении газовой смеси или о дефлаграции^[17]).

Горение газовой смеси непременно сопровождается также и движением газа. Другими словами, процесс горения представ­ляет собой, отвлекаясь от его химической стороны, также и газо­динамический процесс. В общем случае для определения режима горения необходимо совместное решение системы уравнений, включающей в себя как уравнения химической кинетики данной реакции, так и уравнения движения газовой смеси.

Положение, однако, существенно упрощается в том весьма важном случае (с которым обычно и приходится иметь дело), когда характерные размеры /, определяющие условия данной конкретной задачи, достаточно велики (по сравнению с чем именно, будет выяснено ниже). Мы увидим, что в таких случаях чисто газодинамическая задача может быть в известном смысле отделена от задачи химической кинетики.

Область сгоревшего газа (т. е. область, в которой реакция уже закончилась и газ представляет собой смесь продуктов го­рения) отделена от газа, в котором горение еще не началось,, некоторым переходным слоем, где как раз и происходит самая реакция (зона горения или пламя); с течением времени этот слой передвигается вперед со скоростью, которую можно на­звать скоростью распространения горения в газе. Величина ско­рости распространения зависит от интенсивности теплопередачи из зоны горения в ненагретую исходную газовую смесь, причем основной механизм теплопередачи состоит в обычной теплопро­водности (В. А. Михельсон, 1890).

Порядок величины ширины зоны горения б определяется сред­ним расстоянием, на которое успевает распространиться выде­ляющееся в реакции тепло за то время т, в течение которого длится эта реакция (в данном участке газа). Время т есть ве­личина, характерная для данной реакции, и зависит лишь от термодинамического состояния горящего газа (но не от харак­теристических параметров / задачи). Если % — температуропро­водность газа, то имеем см. (51,6):')

6~Ухт~- (128,1)-

Уточним теперь сделанное выше предположение: мы будем считать, что характерные размеры задачи велики по сравнению с толщиной зоны горения (/3>б). При соблюдении этого усло­вия можно выделить чисто газодинамическую задачу. При опре­делении движения газа можно пренебречь толщиной зоны горе­ния и рассматривать ее просто как поверхность, разделяющую продукты горения и несгоревший газ. На этой поверхности (фронт пламени) состояние газа испытывает скачок, т. е. она представляет собой своеобразную поверхность разрыва.

Скорость перемещения v\ этого разрыва относительно самого газа (в нормальном к фронту направлении) называют нормаль­ной скоростью пламени. За время т горение успевает распро­страниться на расстояние порядка величины 6; поэтому искомая скорость пламени•):

_Vl~6/T~Mx)^m. (128,2)

Обычная температуронроводность газа — порядка величины про­изведения длины свободного пробега молекул на их тепловую скорость, или, что то же, произведения времени свободного про­бега Тсв на квадрат скорости. Имея в виду, что тепловая ско­рость молекул совпадает по порядку величины со скоростью зву­ка, найдем:

vJc-Mxc^-iTjTf^[18].

Отнюдь не каждое столкновение молекул сопровождается хими­ческой реакцией между ними; напротив, в реакцию вступает лишь очень незначительная доля сталкивающихся молекул. Это значит, что Тсв <С т и потому v\ <С с. Таким образом, в рассмат­риваемом режиме скорость распространения пламени мала по сравнению со скоростью звука^[19]).

На поверхности разрыва, заменяющего собой зону горения, как и на всяком вообще разрыве, должны выполняться условия непрерывности потоков вещества, импульса и энергии. Первое из этих условий, как обычно, определяет отношение нормальных к поверхности разрыва компонент скорости газа относительно разрыва: $\v\ — p₂t>2, или

vJv^VJVz, (128,3)

где Vi, V2 — удельные объемы несгоревшего газа и продуктов горения. Согласно общим результатам, полученным в § 84 для произвольных разрывов, при наличии скачка нормальной ско­рости касательная компонента скорости должна быть непре­рывна. Поэтому линии тока преломляются на поверхности раз­рыва.

') Для примера укажем, что скорость распространения пламени в смеси 6 °/о СН₄ и 94 % воздуха составляет всего 5 см/с, а в гремучей смеси (2Нг + Ог) — 1000 см/с; ширина зоны горения в этих двух случаях — соот­ветственно ~5-10~² и 5-Ю^-4 см.

Благодаря малости нормальной скорости распространения пламени по сравнению со скоростью звука условие непрерыв­ности потока импульса сводится к непрерывности давления, а потока энергии — к непрерывности тепловой функции:

pi = p₂, w_t = w₂. (128,4)

При использовании этих условий следует помнить, что газы по обе стороны рассматриваемого разрыва химически различны, а потому их термодинамические величины не являются одинако­выми функциями друг от друга. Считая газ политропным, имеем:

wi = wm + Ср\Т\, w₂ = w₀₂ + с_р2Т₂;

аддитивные постоянные нельзя полагать здесь равными нулю, как мы это делали в случае одного газа (выбирая соответствую­щим образом начало отсчета энергии), поскольку здесь w₀\ и w₀₂ различны. Введем обозначение wa\ — w₀₂ — q\ q есть не что иное, как теплота, выделяющаяся при реакции (отнесенная к единице массы), если бы эта реакция происходила при абсолютном нуле температуры. Тогда получаем следующие соотношения между термодинамическими величинами исходного (газ /) и сгоревшего (газ 2) газов:

Наличие определенной нормальной скорости распространения пламени, не зависящей от скоростей движения самого газа, при­водит к установлению определенной формы фронта пламени при стационарном горении в движущемся потоке газа. Примером яв­ляется горение газа, вытекающего из конца трубки (отверстия горелки). Если v есть средняя (по сечению трубки) скорость газа, то очевидно, что viSi = vS, где 5 — площадь поперечного сечения трубки, a Si — полная площадь поверхности фронта пламени.

Возникает вопрос о границах устойчивости описанного режи­ма по отношению к малым возмущениям — условиях реального его существования. Благодаря малости скорости движения газа по сравнению со скоростью звука, при исследовании устойчи­вости фронта пламени можно рассматривать газ как несжи­маемую идеальную (невязкую) среду, причем нормальная ско­рость распространения пламени предполагается заданной по­стоянной величиной. Такое исследование приводит к результату о неустойчивости фронта (Л. Д. Ландау, 1944; см. задачу 1 к этому параграфу). В таком виде это исследование относится лишь к достаточно большим значениям чисел Рейнольдса Ivi/vj и lv₂/v2. Учет вязкости газа, однако, в данных условиях сам посебе не может привести к очень большому критическому значе­нию этих чисел.

Такая неустойчивость должна была бы приводить к самопро­извольной турбулизации пламени. Между тем эксперименталь­ные данные свидетельствуют о том, что самопроизвольная тур-булизация пламени фактически не происходит, — во всяком слу­чае вплоть до очень больших значений числа Рейнольдса. Это связано с наличием в реальных условиях ряда факторов (гидро­динамических и диффузионно-тепловых), стабилизирующих пламя. Изложение этих сложных вопросов выходит за рамки этой книги, и мы ограничимся здесь лишь краткими замечаниями о некоторых из возможных источников стабилизации.

Существенную роль в качестве такого источника может иг­рать влияние искривления фронта на скорость горения. Если учитывать только теплопроводность, то на вогнутых (по отно­шению к исходной горючей смеси) участках фронта скорость v\ повышается (благодаря улучшению условий теплопередачи в охватываемую вогнутостью свежую смесь), а на выпуклых ме­стах v\ уменьшается; этот эффект стремится выровнять фронт, т. е. влияет в стабилизирующем направлении. Изменение же диффузионного режима, как это следует из аналогичных сооб­ражений, оказывает дестабилизирующее действие. Таким обра­зом, общий знак эффекта зависит от соотношения между коэф­фициентами температуропроводности и диффузии (И. П. Дроз­дов, Я. Б. Зельдович, 1943). Для феноменологического описания влияния искривления фронта на скорость горения v\ можно ввести в нее слагаемое, пропорциональное кривизне фронта (G. Н. Markstein, 1951); при надлежащем знаке этого члена его введение в граничные условия на фронте горения приводит к устранению неустойчивости возмущений с малыми длинами волн^[20]). Развитие неустойчивых (в линейном приближении) воз­мущений может стабилизироваться на определенном стационар­ном (по их амплитуде) пределе за счет нелинейных эффектов (R. Е, Petersen, N. W. Emmons, 1956; Я. Б. Зельдович, 1966); этот механизм может привести к «ячеистой» структуре пла­мени ^[21]).

Распространяющееся по горючей смеси пламя приводит в движение окружающий газ на значительном протяжении. Неиз­бежность возникновения сопутствующего горению движения вид­на уже из того, что ввиду различия между скоростями v\ и гь

- 3

I-

Рис. 131

продукты горения должны двигаться относительно несгоревшега газа со скоростью V\ — v₂. В ряде случаев это движение приво­дит также и к возникновению ударных волн. Они не имеют не­посредственного отношения к процессу горения, и их возникно­вение связано с невозможностью удовлетворить иным обра­зом необходимым граничным условиям. Рассмотрим, например* горение, распространяющееся от закрытого конца трубы. На рис. 131 ab есть зона горения. Газ в об-ластях 1 к 3 есгь исходная несгорев-щая газовая смесь, а в области 2— продукты горения. Скорость Vi пере­движения зоны горения относительно находящегося перед ним газа 1 есть величина, определяющаяся свойствами реакции и условиями теплопередачи, и

должна рассматриваться как заданная. Скорость v₂ движения пламени относительно газа 2 определится после этого непосред­ственно условием (128,3). На закрытом конце трубы скорость газа должна обращаться в нуль; поэтому во всей области 2 газ будет неподвижным. Газ же / должен, следовательно, Двигаться относительно трубы с постоянной скоростью, равной v₂ — v\. В передней части трубы вдали от пламени газ тоже должен быть неподвижным. Удовлетворить этому условию можно, толь­ко вводя ударную волну (cd на рис. 131), в которой скорость газа испытывает скачок, так что газ 3 оказывается неподвиж­ным. По заданному скачку скорости определяются также и скач­ки остальных величин, и скорость распространения самой вол­ны. Таким образом, мы видим, что распространяющийся фронт пламени действует как поршень, толкающий находящийся перед ним газ. Ударная волна движется быстрее пламени, так что ко­личество вовлекаемого в движение газа с течением времени воз­растает ').

При достаточно больших значениях числа Рейнольдса сопут­ствующее горению движение газа в трубе становится турбулент­ным, что в свою очередь оказывает обратное турбулизирующее действие на пламя. В вопросах о турбулентном горении еще много неясного, и они здесь не будут рассматриваться.

Задачи

1. Исследовать устойчивость плоского фронта пламени при медленном горении по отношению к малым возмущениям.

Решение. Рассматриваем плоскость разрыва (фронт пламени) в си­стеме координат, в которой он покоится (и совпадает с плоскостью уг); не­возмущенная скорость газа направлена в положительном направлении оси к. На движение с постоянными скоростями v_t, v₂ (по обе стороны разрыва) на­кладываем возмущение, периодическое по времени и по координате у. Из уравнений движения

Дата добавления: 2014-11-07