Должно быть 15 страница

Перенос тепла нормальным движением жидкости представ­ляет собой механизм теплопередачи в гелии II. Он'имеет, таким образом, своеобразный конвективный характер, принципиально отличный от обычной теплопроводности. Всякая разность тем­ператур в гелии II приводит к возникновению в нем внутренних нормальных и сверхтекучих движений; при этом оба потока (сверхтекучий и нормальный) могут компенсировать друг друга по количеству переносимой ими массы, так что никакого реаль­ного макроскопического переноса массы в жидкости может и не быть.

В дальнейшем мы будем обозначать скорости сверхтекучего и нормального движений соответственно как v_s и \_п. Описанный механизм переноса тепла означает, что плотность потока энтро­пии равна произведению v_rtps скорости v„ на энтропию единицы объема жидкости (s — энтропия, отнесенная к единице ее мас­сы). Плотность потока тепла получается соответственно умно­жением потока энтропии на Т, т. е. равна

q = prsv_a.

(137,1)

Свойство потенциальности сверхтекучего движения выражает­ся равенством

rotv_s = 0, (137,2)

которое должно иметь место в любой момент времени во всем объеме жидкости. Это свойство является макроскопическим вы­ражением той особенности энергетического спектра гелия II, ко­торая лежит в основе микроскопической теории сверхтекучести: элементарные возбуждения, обладающие большой длиной волны (т. е. малыми импульсами и энергиями), являются звуковыми квантами — фононами. Поэтому макроскопическая гидродина­мика сверхтекучего движения не должна допускать никаких дру­гих колебаний, кроме звуковых, что и обеспечивается условием (137,2)')-

В силу потенциальности сверхтекучее движение жидкости не оказывает никакой силы на стационарно обтекаемое твердое тело (парадокс Даламбера; см. § 11). Напротив, нормальное движе­ние приводит к возникновению действующей на обтекаемое тело силы сопротивления. Если движение жидкости таково, что сверх­текучий и нормальный потоки массы взаимно компенсируются, то мы получим весьма своеобразную картину: на погруженное в гелий II тело будет действовать сила, в то время как никакого суммарного переноса массы жидкости нет.

Задача

Между концами капилляра с гелием II поддерживается малая разность температур ДГ. Определить тепловой поток, распространяющийся вдоль ка­пилляра.

Решение. Согласно формуле (138,3) перепад давления между обоими концами капилляра Др = ps ДГ. Этот перепад создает в капилляре нормаль­ное движение, средняя (по сечению) скорость которого равна

v_n = R² Др/8т|/

(R — радиус, I — длина капилляра, г| — вязкость нормального движения; ср. (17,10)). Полный тепловой поток равен

8г|/

TnR*p²s² ДГ

Tpsv_nnR² ■■

В обратном направлении возникает сверхтекучее движение, скорость которого определяется условием отсутствия суммарного переноса массы: v_s —

— —VnPnlps-

§ 138. Термомеханический эффект

') Более полное микроскопическое обоснование этого утверждения — см. IX § 26.

Так называемый термомеханический эффект в гелии II за­ключается в том, что при вытекании гелия из сосуда через тон­кий капилляр в сосуде наблюдается нагревание; наоборот, в месте втекания гелия из капилляра в другой сосуд наблюдается охлаждение¹). Это явление естественным образом объясняется тем, что движение вытекающей через капилляр жидкости в ос­новном сверхтекуче и потому не уносит с собой тепла, так что имеющееся в сосуде тепло распределяется на меньшее количе­ство гелия II. При втекании гелия в сосуд имеет место обратное явление.

Легко найти количество тепла Q, поглощающееся при втека­нии в сосуд через капилляр 1 г гелия. Втекающая жидкость не приносит с собой энтропии. Для того чтобы находящийся в со­суде гелий остался при своей температуре Т, надо было бы со­общить ему количество тепла Ts так, чтобы скомпенсировать уменьшение приходящейся на единицу массы энтропии благо­даря введению 1 г гелия с равной нулю энтропией. Это значит, что при втекании 1 г гелия в сосуд с гелием при температуре Т поглощается количество тепла

Q = Ts. (138,1)

Наоборот, при вытекании 1 г гелия из сосуда с гелием при тем­пературе Т выделяется количество тепла Ts.

Рассмотрим теперь два сосуда с гелием II при температурах Т] и Т₂, причем сосуды соединены друг с другом тонким капил­ляром. Благодаря возможности свободного сверхтекучего пере­текания по капилляру быстро установится механическое равно­весие жидкости в обоих сосудах. Поскольку, однако, сверхтеку­чее движение не переносит тепла, тепловое равновесие (при ко­тором температуры гелия в обоих сосудах сравниваются) уста­новится лишь значительно позднее.

Условие механического равновесия легко написать, восполь­зовавшись тем, что установление этого равновесия происходит согласно предыдущему при постоянных энтропиях si и s₂ гелия в обоих сосудах.

Если Ei и г₂— внутренние энергии единицы массы гелия при температурах Т_х и Т₂, то условие механического равновесия (условие минимума энергии), осуществляемого сверхтекучим пе­ретеканием жидкости, будет

(дг, \ _ (де₂ \ \ дЫ Л, V dN)_Sl'

') Весьма слабый термомеханический эффект должен, строго говоря, иметь место и в обычных жидкостях; аномальным у гелия II является боль­шая величина этого эффекта. Термомеханический эффект в обычных жидко­стях представляет собой необратимое явление типа термоэлектрического эф­фекта Пельтье (фактически такой эффект наблюдается в разреженных газах; см. X, задача 1 к § 14). Такого рода эффект должен существовать и в ге­лии II, но в этом случае он перекрывается значительно превосходящим его описанным ниже другим эффектом, специфическим для гелия II и не имею­щим ничего общего с необратимыми явлениями типа эффекта Пельтье.

"где N — число атомов в I г гелия. Но производная (de/6W)_s есть химический потенциал р. Поэтому -мы получаем условие равновесия в виде

|i(Pi,7i) =,i(p_t,r,) (138,2)

(Рь Рг— давления в обоих сосудах).

В дальнейшем мы будем понимать под химическим потен­циалом р не термодинамический потенциал, отнесенный к одной частице (атому), как это обычно принято, а термодинамический потенциал, отнесенный к единице массы гелия; оба определения отличаются лишь постоянным множителем — массой атома гелия.

Если давления р\, р₂ малы, то, разлагая по их степеням и помня, что (дц/др)_т есть удельный объем (слабо зависящий от температуры), получаем:

г,

4г=М0, 7V-n(0, T₂) = \sdT,

где Ар — р2 — р\. Если мала также и разность температур АТ = Т₂ — Т_ь то, разлагая по степеням ДГ и замечая, что (дц,/дТ)_р = —s, получим следующее соотношение:

|f = PS (138,3)

(Н. London, 1939). Поскольку s > 0, то и Др/ДГ > 0.

§ 139. Уравнения гидродинамики сверхтекучей жидкости

Перейдем теперь к выводу полной системы гидродинамиче­ских уравнений, которые описывают движение гелия II макро­скопическим (феноменологическим) образом. Согласно изложен­ным выше представлениям речь идет о составлении уравнений движения, описывающегося в каждой точке не одной, как в обычной гидродинамике, а двумя скоростями v_s и v„. Оказы­вается, что искомая система уравнений может быть получена вполне однозначным образом, исходя из одних только требова­ний, налагаемых принципом относительности Галилея и необхо­димыми законами сохранения (причем используются также свой­ства движения, выражаемые уравнениями (137,1) и (137,2)).

Следует иметь в виду, что фактически гелий II теряет свой­ство сверхтекучести при достаточно больших скоростях движе­ния. Ввиду этого явления критических скоростей уравнения гид­родинамики сверхтекучего гелия обладают реальным физическимсмыслом лишь для не слишком больших скоростей v_s и v„^[73]). Тем не менее мы проведем сначала вывод этих уравнений, не де­лая никаких предположений о скоростях v_s и v„, так как при пренебрежении высшими степенями скоростей теряется возмож­ность последовательного вывода уравнений, исходя из законов сохранения. Переход к физически интересному случаю малых скоростей будет произведен в получающихся окончательных уравнениях.

Обозначим посредством j плотность потока массы жидкости; эта величина является в то же время импульсом единицы ее объема (ср. примечание на стр. 276). Напишем j в виде суммы

п

j = p_sv_s + p„v,

(139,1)

потоков, связанных соответственно с сверхтекучим и нормаль­ным движениями. Коэффициенты p_s и р„ можно назвать сверх­текучей и нормальной плотностями жидкости. Их сумма равна истинной плотности р гелия II:

Р = Ps + рл.

(139,2)

Величины p_s и р„ являются, разумеется, функциями темпера­туры; р„ обращается в нуль при абсолютном нуле, когда ге­лий II «целиком сверхтекуч»^[74]), a p_s обращается в нуль в Я-точке, когда жидкость становится «целиком нормальной».

Плотность р и поток j должны удовлетворять уравнению не­прерывности

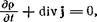
(139,3)

выражающему закон сохранения массы. Закон сохранения им­пульса представляется уравнением вида

d£- + iMi*L = o, (139,4)

dt ^[75] dx_k \ • /

где П;* —тензор плотности потока импульса.

Мы не будем рассматривать пока диссипативных процессов в жидкости; тогда движение обратимо и должна сохраняться также и энтропия жидкости. Имея в виду, что поток энтропии равен psvn, напишем уравнение сохранения энтропии в виде

■^^5L + div(psv_B) = 0. (139,5)

К уравнениям (139,3)—(139,5) должно еще быть добавлено уравнение, определяющее производную по времени от скорости v_s. Это уравнение должно быть составлено таким образом, чтобы обеспечить сохранение со временем потенциальности движения: это значит, что производная v_s должна выражаться в виде гра­диента некоторого скаляра. Мы напишем это уравнение в виде

д\, (vi \

-ьт + Л-т ⁺»)=⁰' ⁽¹³⁹'⁶⁾

где ц. — некоторый скаляр.

Уравнения (139,4) и (139,6) приобретут реальный смысл, ра­зумеется, лишь после того, как будет установлен вид пока не определенных величин П.,-*; и ц. Для этой цели надо использо­вать закон сохранения энергии и соображения, основанные на принципе относительности Галилея. Именно, необходимо, чтобы гидродинамические уравнения (139,3—6) автоматически приво­дили к выполнению закона сохранения энергии, выражающегося уравнением вида

-|^ + divQ = 0, (139,7)

где Е — энергия единицы объема жидкости и Q — плотность по­тока энергии. Принцип же относительности Галилея дает воз­можность определить зависимость всех величин от одной из ско­ростей (v_s) при заданном значении относительной скорости v„ — v_s обоих одновременно происходящих в жидкости дви­жений.

Введем наряду с исходной системой координат К еще и дру­гую систему, Ко, в которой скорость сверхтекучего движения данного элемента жидкости равна нулю. Система Ко дви­жется относительно системы К со скоростью, равной скорости v_s сверхтекучего движения в исходной системе. Значения всех величин в системе К связаны с их значениями в системе Ко (ко­торые мы отличаем индексом нуль) следующими известными из механики формулами преобразования'):

j = pv_s + j₀. £• = — + joVs + Яо.

/ ро? \ vi (139,8)

Q = + JoV_s + Е₀) v_s + -f j₀+ (n₀v_s) + Qo,

n_/ft = pv_siv_sh + v_sij_0k + v_skj_0i + ll_m

(здесь (Ilov_s) обозначает вектор с компонентами По;*у«*)-

В системе Ко данный элемент жидкости совершает лишь одно движение—нормальное движение со скоростью \„ — v_s.Поэтому все относящиеся к этой системе величины j₀, Е₀, Q₀, По<* могут зависеть лишь от разности \„ — \_s, а не от каждой из скоростей v„, Vj в отдельности; в частности, векторы j₀ и Q₀ должны быть направлены вдоль вектора v„ — v.,. Таким образом, формулы (139,8) определяют зависимость искомых величин от v_s при за­данном \_п — V_s.

Энергия Е₀, рассматриваемая как функция от р, s и импульса ^единицы объема жидкости, удовлетворяет термодинамическому соотношению

dE₀ = fi dp + Td (ps) + (v„ - v_s) dj₀, (139,9)

где ц — химический потенциал (термодинамический потенциал единицы массы). Первые два члена соответствуют обычному термодинамическому соотношению для дифференциала энергии неподвижной жидкости при постоянном (здесь — равном еди­нице) объеме, а последний член выражает тот факт, что произ­водная от энергии по импульсу есть скорость движения. Им­пульс j₀ (плотность потока массы в системе Ко) есть, очевидно, просто

jo = P«(v„ — V.,)

(первая из формул (139,8) при этом совпадает с (139,1)).

Ход дальнейших вычислений состоит в следующем. В урав­нение сохранения энергии (139,7) подставляем Е и Q из (139,8),

') Эти формулы являются непосредственным следствием принципа отно­сительности Галилея и потому справедливы вне зависимости от того, о какой именно конкретной системе идет речь. Их можно вывести, рассмотрев, напри­мер, обычную жидкость. Так в обычной гидродинамике тензор плотности по­тока импульса есть П,* — pviv_k + рбц. Скорость жидкости v в системе К связана со скоростью v₀ в системе Ко посредством v = v₀ -f и, где u — ско­рость системы Ко относительно системы К. Подстановка в Пд дает

Введя По;* = рбц -(- pt'ojDo* и jo = pv₀, получим указанную в тексте формулу преобразования для тензора П«. Остальные формулы получаются аналогич­ным образом.

причем производная dE₀/dt выражается через производные от р, ps и j₀ согласно (139,9). После этого все производные по вре­мени (р, v_s и др.) исключаем с помощью гидродинамических уравнений (139,3—6). Довольно громоздкие вычисления приво­дят, после значительных сокращений, к следующему результату:

— П<м4 Ц^- + w_t -~ n_afc -f- р div v_s w Vp + P„w (wV) v„ +

ft ft

+ div (w {Tps + P„p)) + (p„ — ps) w V (ф — ц) = div Qj;

здесь фигурирующий в (139,6) скаляр временно обозначен через ф (вместо р), и для сокращения записи обозначено w — v_n — v_s; кроме того, введено обозначение

р = — E₀+Tps +рр + p„(v„ — Vs)², (139,10)

смысл которого выяснится ниже. Это уравнение сохранения энер­гии должно удовлетворяться тождественно. При этом Q₀, По, ф должны зависеть лишь от термодинамических переменных и от скорости w, но не от каких-либо градиентов этих величин (по­скольку мы не рассматриваем диссипативных процессов). Эти условия определяют выбор выражений для Q₀, П₀, ф однознач­ным образом.

Прежде всего, надо положить ф = р, т. е. фигурирующий в уравнении (139,6) скаляр совпадает с химическим потенциалом жидкости, определенным согласно (139,9) (именно поэтому мы заранее обозначили его буквой р). Для остальных же величин надо положить:

Qo = (Tps + Р„ц) w + p„arV, По/б = pbik + Р_пЩЩ-

Подставив теперь эти выражения в формулы (139,8), получим следующие окончательные выражения для плотности потока энергии и тензора плотности потока импульса:

Q = (p + -|-)j + rpsv„ + p„v_ra(v„, v„-v,>. (139,11)

П,* — PnVnlVnk + PsVslVsk + f&ik- (139,12)

Выражение (139,12) имеет вид, являющийся естественным обобщением формулы = pViVk + p8ik обычной гидродина­мики. При этом величину р, определенную согласно (139,10), естественно рассматривать как давление жидкости; в полностью покоящейся жидкости выражение (139,10) совпадает, разумеет­ся, с обычным определением, так как Ф = р,р становится обыч­ным термодинамическим потенциалом единицы объема жид­кости ').

Уравнения (139,3—6) с определениями j и П\* согласно (139,1), (139,12) представляют собой искомую полную систему гидродинамических уравнений. Эта система очень сложна прежде всего тем, что входящие в уравнения величины p_s, р„, р, s яв­ляются функциями не только термодинамических переменных р и 7", но квадрата относительной скорости обоих движений w² = (\_n — Vs)². Последний представляет собой скаляр, инва­риантный относительно галилеевых преобразований системы от­счета и относительно вращения жидкости как целого; эта вели­чина специфична для сверхтекучей жидкости, отнюдь не должна обращаться в ноль в термодинамическом равновесии, и должна фигурировать в уравнении состояния жидкости наряду с р и Т.

Уравнения, однако, сильно упрощаются в физически интерес­ном случае не слишком больших скоростей (малой величиной предполагается отношение скоростей к скорости второго звука — § HI).

Прежде всего, в этом случае можно пренебречь зависимостью p_s и р„ от w; выражение (139,1) для потока j представляет со­бой при этом по существу первые члены разложения этой вели­чины по степеням v„ и v_s. Разложение по степеням скоростей надо произвести и для остальных термодинамических величин, входящих в уравнения.

Дифференцируя выражение (139,10) и используя (139,9), по­лучим следующее выражение для дифференциала химического потенциала:

dp = - sdT + j dp--^-wdw. (139,13)

Отсюда видно, что первые два члена разложения р по степе­ням w имеют вид

ц(р, Т, w)~p.(p, П--Ц-,ш², (139,14)

где в правой стороне равенства стоят обычные химический по-

') Обычное термодинамическое определение давления как средней силы, действующей на единичную площадку, относится к неподвижной среде. В обыч­ной гидродинамике тем не менее не возникает вопроса об определении поня­тия давления (если не учитываются диссипативные процессы), так как всегда можно перейти к системе координат, в которой данный элемент объема жид­кости покоится. В гидродинамике же сверхтекучей жидкости надлежащим выбором системы координат можно исключить лишь одно из двух одновре­менно происходящих движений, и потому обычное определение давления во­обще не может быть применено.

Отметим также, что выражение (139,10) соответствует и определению давления как производной р = — d(Et>V)/dV от полной энергии жидкости при заданных ее полной массе pV, полной энтропии psV и полном импульсе отно­сительного движения pwV.

тенциал ц(р, 7) и плотность р(р, Т) неподвижной жидкости. Диф­ференцируя это выражение по температуре и давлению, найдем соответствующие разложения для энтропии и плотности:

S(p, T, W)

(139,15)

p (p, T, w) «* p (p, 7") +

Они должны быть подставлены в гидродинамические уравнения, которые после этого будут справедливы с точностью до членов второго порядка по скоростям включительно (учет же в j зави­симости,p_s и р„ от ш² привел бы к членам третьего порядка ма­лости)').

Введение в гидродинамические уравнения членов, учитываю­щих диссипативные процессы в сверхтекучей жидкости, будет произведено в следующем параграфе. Но уже здесь сформу­лируем граничные условия к этим уравнениям.

Прежде всего, на всякой (неподвижной) твердой поверхности должна обращаться в нуль перпендикулярная к этой поверх­ности компонента потока массы j. Для выяснения граничных условий, налагаемых на \_п, надо вспомнить, что нормальное движение есть в действительности движение «газа» элементар­ных тепловых возбуждений в нем. При движении вдоль твер­дой поверхности кванты возбуждения взаимодействуют с ней, что должно быть описано макроскопически как «прилипание» нормальной части массы жидкости к стенке, подобно тому как это имеет место для обычных вязких жидкостей. Другими сло­вами, на твердой поверхности должна обращаться в нуль тан­генциальная компонента скорости v_n.

Что касается перпендикулярной к стенке компоненты v_n, то надо иметь в виду, что кванты возбуждения могут поглощаться или испускаться твердым телом — это соответствует просто теп­лопередаче между жидкостью и твердым телом. Поэтому пер-

') Следует отметить, что система гидродинамических уравнений, в кото­рой p_s рассматривается как заданная функция р и Т, может стать непригод­ной вблизи, лоточки. Дело в том, что при приближении к этой точке (как и ко всякой точке фазового перехода второго рода) неограниченно возрастают время релаксации для установления равновесного значения параметра по­рядка и корреляционный радиус его флуктуации; в сверхтекучем же *Не роль параметра порядка играет конденсатная волновая функция, квадрат модуля которой определяет p_s (см. IV §§ 26, 28; о релаксации в сверхтеку­чей жидкости — см. X § 103). Гидродинамические уравнения с заданной функцией p_s(p, Т) применимы лишь до тех пор, пока характерные расстоя­ния и времена движения велики по сравнению соответственно с корреляцион­ным радиусом и временем релаксации. В противном случае полная система уравнений движения должна включать в себя также я уравнения, опреде­ляющие p_s. См. Гинзбург В. Л., Собянин А. А. — УФН, 1976, т. 120, с. 153; J. Low. Temp. Physics, 1982, v. 49, p. 507.

пендикулярная к стенке компонента скорости v„ не должна не­пременно обращаться в нуль; граничное условие требует лишь непрерывности перпендикулярной к стенке компоненты потока тепла. Температура же испытывает на границе скачок, пропор­циональный тепловому потоку: AT — Kq, с коэффициентом про­порциональности, зависящим от свойств как жидкости, так и твердого тела. Появление этого скачка связано с особенностями теплопередачи в гелии II. Все теплосопротивление между твер­дым телом и жидкостью сконцентрировано в пристеночном слое жидкости, поскольку конвективное распространение тепла в объеме жидкости практически не связано с каким бы то ни было теплосопротивлением; в результате весь перепад температуры, вызывающий появление теплового потока, происходит практи­чески у самой поверхности.

Интересным свойством описанных граничных условий являет­ся то, что теплообмен между твердым телом и движущейся жид­костью приводит к появлению тангенциальных сил, действующих на поверхность тела. Если ось х направлена по нормали, а ось у — по касательной к поверхности, то действующая на единицу площади касательная сила равна компоненте Н_ху тензора потока импульса. Имея в виду, что на поверхности должно быть /* = — PnVnx + psVsx = 0, находим для этой силы отличное от нуля выражение

Rxy =» PsVsxVsy + PnVnxVny = PnVnx(v_ny — V_sy).

Вводя тепловой поток q = psTv_n, можно переписать эту силу

в виде

¹*у ⁼ psT

O_x{v_ny—v_sy),

(139,16)

где q_x — непрерывный на поверхности тепловой поток из твер­дого тела в жидкость.

При отсутствии теплопередачи между твердой стенкой и жид­костью граничное значение перпендикулярной к стенке компо­ненты \_п тоже обращается в нуль. Граничные условия /* = О и v„ = 0 (ось х направлена по нормали к поверхности) эквива­лентны условиям Vsx = 0 и v„ = 0. Другими словами, в этом случае мы получим обычные граничные условия идеальной жид­кости для v_s и вязкой жидкости — для v„.

Наконец, скажем несколько слов о гидродинамике смесей жидкого' Не⁴ с посторонним веществом (фактически — с изо­топом Не³). Помимо уравнений, выражающих сохранение массы, импульса, энтропии и потенциальности сверхтекучего движения, полная система гидродинамических уравнений смеси должна со­держать еще уравнение, выражающее собой сохранение каж­дого из двух веществ по отдельности. Оно имеет вид

д(рс) dt

+ div i О,

f 1401 диссипативные процессы в сверхтекучей жидкости

где с — массовая концентрация Не³ в смеси, a i — плотность его гидродинамического потока. Однако, требования, налагаемые законами сохранения и галилеевой инвариантностью оказывают­ся достаточными для установления вида всех уравнений лишь если известно выражение потока i. Оно дается утверждением о том, что примесь (Не³) принимает участие только в нормаль­ном движении, т. е. i = pcv«').

§ 140. Диссипативные процессы в сверхтекучей жидкости

Для учета диссипативных процессов в уравнениях гидроди­намики сверхтекучей жидкости надо (как и в обычной гидро­динамике) ввести в них дополнительные члены, линейные по про­странственным производным скоростей и температуры. Вид этих членов может быть установлен однозначным образом исходя из требований, налагаемых законом возрастания энтропии и прин­ципом симметрии кинетических коэффициентов Онсагера (И. М. Халатников, 1952).

Как и прежде, р и j — масса и импульс единицы объема жид­кости. Уравнение непрерывности сохраняет свой вид (139,3). В уравнения же (139,4), (139,6—7) надо ввести дополнитель­ные члены, которые напишем в их правых частях;

дП dH_ik dl4 -дТ⁺-Ьх—⁼⁼—^{ШЛ)

ж + v (4 + и) - - W. (140,2)

-|^ + divQ = -divQ'. (140,3)

Энтропийное же уравнение не имеет теперь вида уравнения сохранения (139,5); напротив, величины П', <p', Q' должны быть определены так, чтобы обеспечить возрастание энтропии. Для этого снова подставляем в уравнение сохранения энергии (140,3) производную dE₀/dt, выраженную с помощью (139,9), после чего исключаем производные р, j, v_s с помощью (139,3), (140,1—2). При этом подразумевается, что Q и П даются уже известными выражениями (139,11—12); поэтому сокращаются все члены, за исключением связанных с энтропией и с дис-сипативными величинами П', О/, <р'. В результате получим

') Полный вывод гидродинамических уравнений для смесей — см. книгу Халатникова И. М. Теория сверхтекучести. — М.: Наука, 1971, гл. XIII. Эти уравнения становятся неприменимыми при очень низких температурах, когда возникает квантовое вырождение элементарных возбуждений, связанных с атомами примеси.

уравнение

r{^+div(_PSv„)}== - - div {Q' + p_swq/ - (П'у„)} + _Ф' div (p_sw) - П',[76] -^f- (140,4)

k

(здесь снова w = v„ — v_s).

Линейные по градиентам выражения величин IT, О/, ф', обес­печивающие возрастание энтропии, имеют вид¹):

«.~₄tf£+3?-4«..di".)-

— 6_tkZi div (_Psw) — 6_/A£₂ div v„, (140,5)
9^, = g₃div'_Psw) +?4divv„, (140,6)

Q' = — q>'_Psw + (П'у„) - x (140,7)

(в Пг[77] выделена комбинация производных от v„ с равным нулю следом — подобно тому, как это делается в обычной гидродина­мике). При этом согласно принципу Онсагера должно быть

Si=U (140,8)

так что остается всего 5 независимых кинетических коэффициен­тов²).

Наконец, подставив выражения (140,5—7) в уравнение (140,4), после простых преобразований приведем его к виду

т{^ЁЖ¹ + [78] ™(рзУп-Т [79] ^Г)} = [80]. (Н0,9)

где

+ 2£, div v„ div o,w + Ь (div v„)² + £з (div p_sw)² + -f (V7?. (140,10)

') Здесь учитывается также и условие, что вращение нормальной части жидкости как целого (v„ = [fir]) не должно приводить к диссипации (ср. § 15).

Это уравнение — аналог общего уравнения переноса тепла обыч­ной гидродинамики (49,5)³). Если правая сторона определяет скорость возрастания энтропии жидкости и должна быть суще­ственно положительной величиной. Отсюда следует, что все коэф­фициенты л, £i £2, £₃, х положительны, причем сверх того с,^^₃. Коэффициент т| «первой вязкости», связанный с нор­мальным движением, аналогичен вязкости обычной жидкости, а коэффициент к формально аналогичен теплопроводности обыч­ной жидкости; коэффициентов же «второй вязкости» имеется теперь три (£ь £2. £з) вместо одного в обычной гидродинамике.

По поводу изложенных результатов необходимо, однако, сде­лать еще следующее замечание. Диссипируемая в жидкости энергия разумеется, инвариантна относительно галилеевого пре­образования системы отсчета. Производные от скорости этому требованию конечно удовлетворяют, но в сверхтекучей жид­кости галилеевски инвариантна также и разность скоростей w = V/i — v_s. Поэтому и диссипативные потоки в сверхтекучей жидкости могут зависеть не только от градиентов термодинами­ческих величин и скоростей, но и от самой w. Как уже было от­мечено в § 139, эта разность фактически должна рассматривать­ся как малая величина, и в этом смысле выражения (140,5—6) содержат в себе не все в принципе возможные члены, но лишь наибольшие из них

Дата добавления: 2014-11-07