Должно быть 14 страница

т. е. совпадает, как и следовало, с обычным выражением для плотности потока импульса, который мы обозначали в § 7 по­средством П_ар.

Простая связь между плотностью импульса и плотностью потока энергии (отличие в множителе с²) теряется в нереляти­вистском пределе благодаря тому, что в нерелятивистскую энер­гию не включается энергия покоя. Действительно, компоненты Т^0а/с образуют трехмерный вектор, приближенно равный

pv+4rv(p_e + p + -^).

Отсюда видно, что предельное значение плотности импульса есть, как и следовало, просто pv; для плотности же потока энергии находим, опустив член pc²v, выражение v(pe + Р + рс²/2), совпадающее с найденным в § 6.

§ 134. Релятивистские гидродинамические уравнения

Уравнения движения содержатся, как известно, в уравнениях

дТ^к

-рг = 0. (134,1)

дх

выражающих собой законы сохранения энергии и импульса той физической системы, к которой относится тензор T^ik. Воспользо­вавшись выражением (133,2) для Р^к, мы получим отсюда урав­нения движения жидкости; при этом, однако, необходимо допол­нительно учесть сохранение числа частиц, не содержащееся в уравнениях (134,1). Подчеркнем, что тензор энергии-импульса (133,2) не учитывает никаких диссипативных процессов (в том числе вязкости и теплопроводности); поэтому речь идет об урав­нениях движения идеальной жидкости.

Для формулирования уравнения, выражающего сохранение числа частиц в жидкости (уравнения непрерывности), введем 4-вектор тока частиц п¹. Его временная компонента есть плот­ность числа частиц, а пространственные компоненты составляют трехмерный вектор тока частиц. Очевидно, что 4-вектор п' дол­жен быть пропорционален 4-скорости и,¹, т. е. иметь вид

п¹ = пи⁽, (134,2)

где п — скаляр; из его определения ясно, что п — собственная плотность числа частиц^[34]). Уравнение непрерывности выражается просто равенством нулю 4-дивергенции вектора тока:

д(пи ^[35] )

0. (134,3>

дх'

Возвратимся к уравнениям (134,1). Дифференцируя выраже­ние (133,2), получим

дТ^к diwu") „ du_t dp

^^_Ui.__ ₊ ^_i.___₌₌₀. (134,4)

Умножим это уравнение на и\ т. е. спроецируем его на направ­ление 4-скорости. Помня, что щи' — 1, а потому щди ^[36] /дх^к = О, находим

i^>_„*^ = 0. (134,5>

дх дх

Заменив тождественно wu^k = nu^k(w/n) и воспользовавшись уравнением непрерывности (134,3), переписываем это уравнение в виде

ft Г д w 1 др 1 _п

пи г ^ = 0.

1дх^к п п дх^к J

Согласно известному термодинамическому соотношению для теп­ловой функции имеем

d^.=Td± + ±dp (134,6)

(Т— температура, о — энтропия, отнесенная к единице собствен­ного объема)^[37]). Отсюда видно, что выражение в квадратных скобках есть производная Тд(о/п) /дх^к. Опустив множитель пТ, приходим, таким образом, к уравнению

_B*_^.i_3BJ_i _{= 0}, (134,7)

дх п ds п

выражающему адиабатичность движения жидкости (d/ds озна­чает дифференцирование вдоль мировой линии движения дан­ного элемента жидкости). С помощью уравнения непрерывности (134,3) его можно представить в эквивалентном виде

— au^l = Q, (134,8)

дх

т. е. как равенство нулю 4-дивергенции потока энтропии си'.

Спроецируем теперь уравнение (134,1) на направление, нор­мальное к и¹. Другими словами, составим их комбинацию¹)

i

дТ* _k dT_k

_т — щи—_г = 0

дх^к дх¹

(выражение в левой стороне тождественно обращается в ноль при скалярном умножении на и¹). Простое вычисление приводит к уравнению

,. ди, др ъ др

™*1?=17-^в'"1?- ⁽¹³⁴'⁹⁾

Три пространственные компоненты этого уравнения представ­ляют собой релятивистское обобщение уравнения Эйлера (вре­менная же компонента есть следствие первых трех).

Уравнение (134,9) может быть представлено в другом виде в случае изэнтропического движения (подобно преобразованию от (2,3) к (2,9) для нерелятивистского уравнения Эйлера). При о/п — const имеем, согласно (134,6),

др ^ д w

дх¹ дх¹ п

и уравнение (134,9) принимает вид

«7Т(—"*) = ТТ —• (134,10)

дх \п) дх п

Если движение к тому же еще и стационарно (все величины не зависят от времени), то пространственные компоненты

(134,10) дают

V<vY)(^v) _{+ C}^ = 0.

Умножив это уравнение скалярно на v, после простых преоб­разований получим (vV) (yw/n) — 0. Отсюда следует, что вдоль каждой из линий тока постоянна величина

yw/n = const.

(134,11)

Это — релятивистское обобщение уравнения Бернулли¹).

Не предполагая изэнтропическое течение стационарным, легко видеть, что уравнения (134,10) имеют решения вида

умножив это равенство скалярно на и" и раскрыв производную в правой стороне, действительно вернемся к уравнению (134,10). Пространственные и временная компоненты равенства (134,12) дают:

w _r, w, d<f _A

у—v=vm, су--------------- г--зг = 0-

■ nc ^ ' n ¹ dt

Первое из них в нерелятивистском пределе дает обычное усло­вие потенциальности, а второе — уравнение (9,3) (с соответ­ствующим переобозначением <р/ст->-ф).

Рассмотрим распространение звука в среде с релятивистским уравнением состояния (т. е. в котором давление сравнимо с плот­ностью внутренней энергии, включающей в себя энергию покоя). Гидродинамические уравнения звуковых волн могут быть линеа­ризованы; при этом удобнее исходить непосредственно из записи уравнений движения в исходном виде (134,1), а не из эквива­лентных им уравнений (134,8—9). Подставив выражения (133,3) компонент тензора энергии-импульса и сохранив везде лишь величины первого порядка малости по амплитуде волны, полу­чим систему уравнений

de' dt

= — wdiv\

— — = -Vd'

c² dt ^xp '

(134,13)

где штрихом отмечены переменные части величин в волне. Исключив отсюда v, найдем:

at²

д ^[38] е'

с^[39]г\р\

Наконец, написав ё = (де/др)_ллр', получим для р' волновое уравнение со скоростью звука ')

«=<ш:: ('«.»»

(индекс «ад» указывает, что производная должна быть взята для адиабатического процесса, т. е. при постоянном о/п). Эта формула отличается от соответствующего нерелятивистского вы­ражения тем, что вместо обычной плотности массы здесь стоит е/с^[40]. Для ультра релятивистского уравнения состояния р = е/3 скорость звука и = с/л/З.

Наконец, скажем несколько слов о гидродинамических урав­нениях при наличии существенных гравитационных полей, т. е. в общей теории относительности. Они получаются из уравнений (134,8—9) просто путем замены обычных производных кова-риантными ^[41])

WU^kUf. *= -рг- тт- (*"'): ' = °- (134,15)

дх дх

Выведем из этих уравнений условие механического равнове­сия в гравитационном поле. При равновесии гравитационное поле статично; можно выбрать такую систему отсчета, в которой вещество неподвижно («^а = 0, и° = £₀<Г^1/2), все величины не за­висят от времени, а смешанные компоненты метрического тен­зора равны нулю (goa = 0). Пространственные компоненты уравнения (134,15) дают тогда

_шГо_ыо_{ц =}±_?_䧙^ ЁР_

^{а0 и} 2 g₀₀ дх^а дх*'

или

w дх^а 2 дх^а

1 dp _ I

ngoo- (134,16)

') Которая в этой главе будет обозначаться посредством и.

Это и есть искомое уравнение равновесия. В нерелятивист­ском предельном случае w = рс^[42], g₀₀ — 1 + 2q>/c^[43] (ip — ньютонов­ский гравитационный потенциал), и уравнение (134,16) перехо­дит в

Чр = — рУф, т. е. в обычное гидростатическое уравнение.

Задачи

1. Найти решение гидродинамических уравнений, описывающее одномер­ную нестационарную простую волну.

Решение. В простой волне все величины могут быть выражены в виде функции любой одной из них (см. § 101). Написав уравнения движения в виде

6Тоо дТы _ дТу дТ_и __п

cdt дх ' cdt дх

и считая 7"оо, 7\н, ^тч функциями друг от друга, получим соотношение dTdodTii = (dToi)². В него надо подставить

^roo = ^eul + Р^ии ^T0[=^wua^uu ^гп =«"i + Р"о>

2 2

учитывая при этом, чтощ — u, = 1 (при вычислении удобно ввести параметр т) согласно и₀ = ch r|,»i = — sh ti). В результате вычисления получается:

Arth — = ± — \ — de (2)

С С J W

(и — скорость звука). Далее, из (1) находим:

дх dT_m

dt dT,

и, вычисляя эту производную, получим:

Формулы (2), (3) и определяют искомое решение.

2. Написать гидродинамические уравнения для ультрарелятивистской сре­ды с неопределенным числом частиц (которое само определяется условиями термодинамического равновесия).

Решение. Условие термодинамического равновесия, определяющее чис ла частиц в такой среде состоит в равенстве нулю всех химических потен­циалов. Тогда е — То + р = 0, т. е. w = Та, а согласно термодинамическому выражению дифференциала тепловой функции (при заданном — единичном — объеме и нулевых химических потенциалах) dw = Tda -f dp; комбинируя обе формулы, получим: dp = adTⁱ). Уравнение (134,5) (в котором еще не ис­пользовалось уравнение непрерывности) приводит к уравнению адиабатично-сти в форме (134,8). Уравнение же (134,9) принимает вид

k дТи_{ дТ

U г-= _г.

дх^к дх¹

') При ультрарелятивистском уравнении состояния р = е/3 из написан­ных формул легко найти, что е оо Г⁴, а оо Т^а, т. е. те же законы, которые справедливы для черного излучения (см. V § 63), —как и следовало ожи­дать.

§ 135. Ударные волны в релятивистской гидродинамике

Теория ударных волн в релятивистской гидродинамике строится аналогично нерелятивистской теории (А. Н. Taub, 1948).

Как и в § 85, рассматриваем поверхность разрыва в системе координат, в которой она покоится, а газ движется перпендику­лярно ей (вдоль оси х^х == х) со стороны / на сторону 2. Условия непрерывности плотностей потока частиц, потока импульса и потока энергии гласят:

[п^х] = [пи^х] = 0, [Т^хх] = [а> (и^х) ^[44] + р] = 0,

с [Т^0х] = с [wu°u^x] = О,

или, после подстановки значений компонент 4-скорости:

fiYi/V^tW^^/. (135,1)

да,и^[45]у^[46] + р, ш₂и^[47]у^[48] + р₂, (135,2)

o»₁»iYi = a'2⁰2Y2 (135,3)

где у, = (1 - vyc ^[49] )'¹' ^[50] , Y₂ = (1 - vyc ^[51] )-¹' ^[52] , а К, = 1/д, и V-2—l/n₂— объемы, отнесенные к одной частице '). Из (135,1) и (135,2) находим

/^[53] = (P2-Pi)c^[54]/UiKi-_№l/2). (135,4)

Далее, переписываем условие (135,3) с учетом (135,1) в виде

wtV^[55]y^[56] = w ^[57] V^[58]y^[59].

Путем простых алгебраических преобразований (из (135,1) вы­ражаем у^[60] и у^[61] через j ^[62] , а затем подставляем /^[63] из (135,4)), получим следующее релятивистское уравнение ударной адиа­баты (адиабата Тауба):

w\V\ - w ^[64] V ^[65] + (р₂ - р,) (w_{V ^[66] + w₂V ^[67] ) = 0. (135,5)

Приведем также выражения для скоростей газа по обе сто­роны поверхности разрыва, которые можно получить путем эле­ментарных преобразований из условий (135,2—З)^[68]):

О, r (P2-Pl)(e2+Pl) T'^[69] Р2 Г (Р2 - Pl) (б1 + р₂) I'/^[70] ПОССЧ

') В нерелятивистском пределе определенный согласно (135,1) поток числа частиц отличается множителем 1/т от плотности потока массы, обо­значавшейся через / в § 85. Множителем m отличаются также определенные здесь и в § 85 объемы V.

~7~ L (e«-ei)(ei +Р₂) J ' ^с L(e»-*,)(<>* + /»,) J * ^U '^;

Относительная же скорость газов по обе стороны разрыва со­гласно релятивистскому правилу сложения скоростей равна

₀,_{2 = i}^-^P2_/2 =c\^{_l>^H7^PlU^e2I^e>lT- (135,7)

¹² 1 — viv₂/c² I (е, + pi) (е₂ + Pi) J ^v '

В нерелятивистском пределе, если положить е «mc²n = mc²[V и пренебречь р по сравнению с е, формулы (135,4), (135,6—7) переходят в формулы (85,4), (85,6—7) (с учетом указанной в примечании разницы в определениях / и V здесь и в § 85)¹). Для ультрарелятивистского же уравнения состояния р = е/3 из (135,6) имеем

Oi_ _ Г 3e₂ + ei -11/2 Oj_ _ Г Зе, + ^2 У '² «

с L3 (Зе, + е₂) J ' с b('ie₂ + e_t)}

(отметим, что Dit>2 = с²/3). При увеличении интенсивности удар­ной волны (e2->-oo)rJi стремится к скорости света, a v₂— к с/3.

Подобно тому, как в гл. IX мы изображали ударную адиа­бату графиком в плоскости V, р, так естественными перемен­ными для изображения релятивистской ударной адиабаты яв­ляются wV², рс²; в этих координатах /² определяет наклон хорды, проведенной из начальной точки адиабаты / в произвольную точку 2.

Релятивистские ударные волны слабой интенсивности могут быть рассмотрены вполне аналогично тому, как это было сде­лано в § 86 в нерелятивистском случае (Я. М. Халатников, 1954). Не повторяя заново всех вычислений, приведем резуль­тат для скачка энтропии, который снова оказывается малой ве­личиной третьего порядка по сравнению со скачком давления:

Поскольку должно быть а₂ > а\, то мы видим, что ударная волна является волной сжатия, если

№)»>•■ <'»■'<»

Это условие представляет собой релятивистское обобщение условия (86,2) нерелятивистской гидродинамики²). При р₂> р\

') Для предельного перехода от уравнения адиабаты (135,5) к нереля-тивисткому уравнению (85,10) такое приближение недостаточно; надо поло­жить w = птс^г + птг + р (в — нерелятивистская внутренняя энергия, отне­сенная к единице массы) и, разделив уравнение (135,5) на с², перейти к пре­делу с -*- оо.

²) Используя термодинамическое соотношение для тепловой функции, отнесенной к одной частице, d(wV) = Vdp (при = const), найдем, что условие (135,10) эквивалентно неравенству

(МЛ _>±\(W\ I V др¹;_ая «"IV др Лд I

В нерелятивистском пределе правая сторона заменяется нулем.

из (135,4) и (135,5) следует, что

w₂V\<w_xV², w₂V₂>w_lV₁;

отсюда, в свою очередь, следует, что во всяком случае Vz < Vi,— объем V должен уменьшиться даже сильнее, чем wV возрастает. Скорости v\ и t>2 ударной волны слабой интенсивности в первом приближении совпадают, естественно, со скоростью звука: по­скольку изменение энтропии — величина третьего порядка, то выражения (135,6) при р₂-+Ръ e₂-*-ei переходят в производ­ную (134,14)'). Рассуждения, вполне аналогичные произведен­ным в § 86, показывают, что в следующем приближении v\ > и\,

V2 <U₂.

Таким образом, направление изменения величин в реляти­вистской ударной волне слабой интенсивности подчиняется (при условии (135,10)) тем же неравенствам, что и в нерелятивист­ском случае. Обобщение этого результата на ударные волны произвольной интенсивности оказывается возможным произвести способом, вполне аналогичным примененному в § 87 ²).

Подчеркнем в то же время, что неравенства v_x > щ и v₂ < «г справедливы для релятивистских (как и для нерелятивистских) ударных волн вне зависимости от каких бы то ни было термоди­намических условий — как следствие требования эволюцион-ности. Напомним, что при выводе этих условий (§ 88) был суще­ствен только знак скоростей и ± v распространения звуковых возмущений в движущейся жидкости по отношению к неподвиж­ной поверхности разрыва. Согласно релятивистскому правилу сложения скоростей эти скорости даются выражениями (и ± v)/(l ± vu/c²), знак которых определяется только их чис­лителями, так что все проведенные в § 88 рассуждения остаются в силе.

§ 136. Релятивистские уравнения движения вязкой и теплопроводной среды

Установление релятивистских гидродинамических уравнений при наличии диссипативных процессов (вязкости и теплопро­водности) сводится к вопросу об определении вида соответствую­щих дополнительных членов в тензоре энергии-импульса и в векторе плотности потока вещества. Обозначая эти члены

^!) Выражение же (135,4) переходит в производную — cⁱ\dpld(wV'^l)]\. С помощью термодинамических выражений d(eV) ——pdV, d(wV) = Vdp (при aV = const) легко убедиться, что эта производная, умноженная на V\, равна, как и следовало, в²/(l — и²).

^s) См. Thome K.S. — Astroph. J., 1973, v. 179, p. 897.

соответственно как г,-* и vt, напишем:

Tik==pgtk + wu_tu_k + x_ik, (136,1)

n_l = nu_i + v_l. (136,2)

Уравнения движения по-прежнему содержатся в

дТ1 дп¹

—4- = 0, —7=0.
дх^к дх¹

Прежде всего, однако, возникает вопрос о более точном опре­делении самого понятия скорости и¹. В релятивистской механике всякий поток энергии неизбежно связан также и с потоком массы. Поэтому при наличии, например, теплового потока опре­деление скорости по потоку массы (как в нерелятивистской гид­родинамике) теряет непосредственный смысл. Мы определим здесь скорость условием, чтобы в собственной системе отсчета каждого данного элемента жидкости его импульс был равен нулю, а его энергия выражалась через другие термодинамиче­ские величины теми же формулами, как и при отсутствии дисси-пативных процессов. Это значит, что в указанной системе отсчета должны обращаться в нуль компоненты тоо и то_а тензора t«v, поскольку в этой системе и и^а = 0, то имеем в ней (а потому и в любой другой системе) тензорное соотношение

т«н* = 0. (136,3)

Аналогичное соотношение

v,m' = 0 (136,4)

должно выполняться и для вектора v,-, поскольку в собственной системе отсчета компонента п° 4-вектора потока частиц п¹ долж­на, по определению, совпадать с плотностью числа частиц п.

Искомый вид тензора t,-& и вектора v, можно установить, ис­ходя из требований, налагаемых законом возрастания энтропии. Этот закон должен содержаться в уравнениях движения (по­добно тому как в § 134 из этих уравнений получалось для иде­альной жидкости условие постоянства энтропии). Путем про­стых преобразований с использованием уравнения непрерывности легко получить следующее уравнение:

, аг* д. dv¹ _s бч?

где д. — релятивистский химический потенциал вещества: пц~ = w — Та, и использовано термодинамическое соотношение для его дифференциала:

dp^La-p — S-dT. ■ (136,5)

Наконец, используя (136,3), перепишем это уравнение в виде

д (, Ц \.да i^k ди¹

—_т(аи¹- — v4 = -v'-_T — + -L-. (136,6)
дх¹ \ Т) дх Т Т дх

Стоящее слева выражение должно представлять собой 4-ди-вергенцию потока энтропии, а выражение справа — возрастание энтропии вследствие диссипатиЕных процессов. Таким образом, 4-вектор плотности потока энтропии есть

a¹ = au^l --^ v\ (136,7).

a %ik и V' должны выражаться линейно через градиенты скорости и термодинамических величин так, чтобы обеспечить существен­ную положительность правой стороны уравнения (136,6). Это условие вместе с условиями (136,3—4) однозначно определяет вид симметричного 4-тензора т,* и 4-вектора v,-:

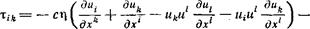
-c{l-\^)^{g_ik-u_iUk), (136,8)

Здесь r|, £ — два коэффициента вязкости, ах — коэффициент теп­лопроводности, выбранные в соответствии с их нерелятивистским определением. В нерелятивистском пределе компоненты т_ар сво­дятся к компонентам трехмерного тензора вязких напряжений с_й9 (15,3).

Чистой теплопроводности соответствует поток энергии при отсутствии потока вещества. Условие последнего есть riu^aJr -f- _v^a = 0. При этом пространственные компоненты 4-скорости ы«= —v^a/n — величины первого порядка по градиентам; по­скольку выражения (136,8—9) написаны лишь с точностью до величин этого порядка, компоненту и⁰ 4-скорости надо положить равной единице: и\ — 1 + и_аи^а = 1 + v_av^a/«² «* 1. С этой же точ­ностью надо опустить второй член в квадратных скобках в (136,9). Тогда для плотности потока энергии сТ^0а — — cT^Q_a на ходим:

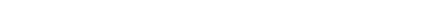
получим поток энергии:

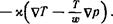
(136,10)

Мы видим, что в релятивистском случае теплопроводностный по­ток тепла пропорционален не просто градиенту температуры, а определенной комбинации градиентов температуры и давления (в нерелятивистском пределе ш ж птс² и член с Vp должен быть опущен).

ГЛАВА ХУГ

ГИДРОДИНАМИКА СВЕРХТЕКУЧЕЙ ЖИДКОСТИ

§ 137. Основные свойства сверхтекучей жидкости

При температурах, близких к абсолютному нулю, в свой­ствах жидкости на первый план выдвигаются квантовые эф­фекты; в таких случаях говорят о квантовых жидкостях. Фак­тически лишь гелий остается жидким вплоть до абсолютного нуля; все другие жидкости затвердевают значительно раньше, чем в них становятся заметными квантовые эффекты. Суще­ствуют, однако, два изотопа гелия —⁴Не и ³Не, отличаю­щиеся статистикой, которой подчиняются их атомы. Ядро ⁴Не не имеет спина, и вместе с ним равен нулю и спин атома в целом; эти атомы подчиняются статистике Бозе — Эйнштейна. Атомы же ³Не обладают (за счет своего ядра) спином '/₂ и подчи­няются статистике Ферми — Дирака. Это различие имеет фун­даментальное значение для свойств образуемых этими веще­ствами квантовых жидкостей; в первом случае говорят о кван­товой бозе-жидкости, а во втором — о ферми-жидкости. В этой главе будет идти речь только о первой из них.

При температуре 2,19 К жидкий гелий (изотоп ⁴Не) имеет так называемую Я-точку (фазовый переход второго рода)^[71]). Ниже этой точки жидкий гелий (в этой фазе его называют Не II) обладает рядом замечательных свойств, из которых наиболее су­щественным является открытая П. Л. Капицей в 1938 г. сверх­текучесть — свойство протекать по узким капиллярам или ще­лям, не обнаруживая никакой вязкости.

Теория сверхтекучести была развита Л. Д. Ландау (1941). Ее микроскопическая часть изложена в другом томе этого Курса (см. IX глава III). Здесь же мы остановимся лишь на макроско­пической гидродинамике сверхтекучей жидкости, которая может быть построена на базе представлений микроскопической тео­рии ^[72]).

Отправным пунктом гидродинамики гелия II является сле­дующий основной результат микроскопической теории. При от-

§ 137)

ОСНОВНЫЕ СВОЙСТВА СВЕРХТЕКУЧЕЙ ЖИДКОСТИ

личных от нуля температурах гелий II ведет себя так, как если бы он представлял собой смесь двух различных жидкостей. Одна из них сверхтекуча и при движении вдоль твердой поверхности не обнаруживает никакой вязкости. Другая же ведет себя, как обычная нормальная вязкая жидкость. При этом весьма суще­ственно, что между обеими этими движущимися «друг через друга» частями массы жидкости нет трения, т. е. не происходит передачи импульса от одной из них к другой.

Следует, однако, самым решительным образом подчеркнуть, что рассмотрение жидкости как смеси нормальной и сверхтеку­чей ее частей является не более чем способом наглядного описа­ния явлений, происходящих в квантовой жидкости. Как и вся­кое описание квантовых явлений в классических терминах, оно не вполне адекватно. В действительности надо говорить, что в квантовой жидкости — гелии II — может существовать одновре­менно два движения, каждое из которых связано со своей эф­фективной массой (так что сумма обеих этих масс равна полной истинной массе жидкости). Одно из этих движений нормально, т. е. обладает теми же свойствами, что и движение обычной вяз­кой жидкости; другое же — сверхтекуче. Оба эти движения про­исходят без передачи импульса от одного к другому. В опреде­ленном смысле можно говорить о сверхтекучей и нормальной частях массы жидкости, но это отнюдь ие означает возможности реального разделения жидкости на две части ').

Лишь имея в виду все эти оговорки относительно истинного характера происходящих в гелии II явлений, можно пользовать­ся терминами сверхтекучая часть и нормальная часть жидкости как наглядным способом краткого описания этих явлений. Мы, однако, будем предпочитать пользоваться более точными терми­нами сверхтекучее движение и нормальное движение, не ассо­циируя их с компонентами «смеси» двух «частей» жидкости.

Представление о двух видах движения дает простое объясне­ние наблюдающимся на опыте основным свойствам течения ге­лия II. Отсутствие вязкости при протекании гелия II по узкой щели объясняется тем, что* в щели имеет место сверхтекучее движение жидкости, не обнаруживающее трения; можно сказать, что нормальная часть, задерживается в сосуде, протекая через щель несравненно медленнее, со скоростью, соответствующей ее вязкости и ширине щели. Напротив, измерение вязкости гелия II по затуханию крутильных колебаний погруженного в жидкость диска должно давать отличные от нуля значения: вращение диска создает вокруг него нормальное движение жидкости, ос­танавливающее диск благодаря свойственной этому движению вязкости. Таким образом, в опытах с протеканием по капилляру или щели обнаруживается сверхтекучее движение жидкости, а в опытах с вращением диска в гелии II обнаруживается ее нор­мальное движение.

Помимо отсутствия вязкости, сверхтекучее движение жид­кости обладает еще и следующими двумя важнейшими свой­ствами: оно не сопровождается переносом тепла и всегда потен­циально. Оба эти свойства тоже следуют из микроскопической теории, согласно которой нормальное движение жидкости пред­ставляет собой в действительности движение «газа возбужде­ний»; напомним, что коллективное тепловое движение атомов квантовой жидкости можно рассматривать как совокупность от­дельных элементарных возбуждений, ведущих себя как некото­рые квазичастицы, движущиеся в занимаемом жидкостью объеме и обладающие определенными импульсами и энергиями.

Энтропия гелия II определяется статистическим распределе­нием элементарных возбуждений. Поэтому при всяком движении жидкости, при котором газ квантов возбуждения остается непод­вижным, не возникает никакого макроскопического переноса энтропии. Это и значит, что сверхтекучее движение не сопро­вождается переносом энтропии, или, другими словами, не пере­носит тепла. Отсюда в свою очередь следует, что течение ге­лия II, при котором имеет место лишь сверхтекучее движение, является термодинамически обратимым,

Дата добавления: 2014-11-07