Должно быть 9 страница

§ 120. Обтекание со звуковой скоростью

Упрощенное уравнение Чаплыгина в форме уравнения Эйле­ра — Трикоми должно, в принципе, применяться к исследованию основных качественных особенностей стационарного плоского об­текания тел, связанных с наличием в нем околозвуковых обла­стей. Сюда относятся, в первую очередь, вопросы, связанные с возникновением ударных волн. В околозвуковой зоне интенсив­ность ударной волны мала; подчеркнем, что именно это обстоя­тельство делает законным применение уравнения Эйлера — Трикоми в этих условиях. Напомним (см. §§ 86, 114), что в сла­бой ударной волне изменение энтропии и ротора скорости — величины более высоких порядков малости; поэтому в первом приближении движение можно считать изэнтропическим и по­тенциальным и позади разрыва.

В этом параграфе мы рассмотрим теоретически важный во­прос—о характере стационарного плоского обтекания, когда скорость набегающего потока равна в точности скорости звука.

Мы увидим, что при таком обтекании непременно имеется простирающаяся от тела до бесконечности ударная волна. От­сюда следует важное заключение о том, что ударная волна должна впервые возникнуть при числе Моо, во всяком случае меньшем единицы.

') Здесь надо иметь в виду, что F{a, в, у, г) сводится к полиному, если для а (или Р) имеет место а = —п или у — а —п.

Итак, рассмотрим плоское обтекание тела с бесконечно длин­ным размахом («крыла») произвольного, не обязательно сим­метричного сечения. При этом мы будем интересоваться карти­ной течения на достаточно больших (по сравнению с разме­рами) расстояниях от тела. Для удобства изложения мы сна­чала опишем качественно получающиеся результаты, а затем перейдем к количественному расчету. На рис. 122 АВ и А'В' — звуковые линии, так что слева от них (вверх по течению) лежит целиком дозвуковая область; стрелкой изображено направление натекающего потока (которое мы ниже выбираем в качестве оси х с началом где-либо в районе тела). На некотором расстоя­нии от линии перехода возникают «ис­ходящие» от тела ударные волны (EF и E'F' на рис. 122). Оказывается, что все исходящие от тела характери- ^х стики (в области между линией пере­хода и ударной волной) можно разде­лить на две группы. Характеристики первой группы достигают звуковой ли­нии, оканчиваясь на ней (или, иначе говоря, отражаясь от нее в виде харак­теристики, приходящей к телу; на рис. 122 изображена одна из таких ха­рактеристик). Характеристики же вто­рой группы оканчиваются на ударной волне. Обе эти группы разделены предельными характери­стиками— единственными, уходящими на бесконечность и никогда не достигающими ни звуковой линии, ни удар­ной волны (CD и CD' на рис. 122). Поскольку возмущения (связанные, например, с изменением контура обтекаемого тела), распространяющиеся от тела по характеристикам первой груп­пы, достигают границы дозвуковой области, то ясно, что часть сверхзвукового потока, лежащая между линией перехода и пре­дельной характеристикой, влияет на дозвуковую область; весь же поток в области справа от предельных характеристик ника­кого влияния на поток слева не оказывает: течение слева никак не изменится при возмущении потока справа (в том числе при изменении профиля тела справа от точек С, С). Течение позади ударной волны, как мы знаем, никак не влияет на течение пе­ред ней. Таким образом, весь поток можно разделить на три части (слева от DCCD' между DC CD' и FEE'F', справа от FEE'F'), причем течение во второй никак не влияет на течение в первой, а течение в третьей — на течение во второй.

Перейдем теперь к количественному расчету описанной кар­тины (являющемуся в то же время ее проверкой).

Начало координат в плоскости годографа (8 = л = 0) соот-
ветствует бесконечно удаленной области в физической плоскости,
а выходящие из начала координат годографические характери-
стики соответствуют предельным характеристикам CD и CD'. На
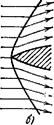
рис. 123 изображена окрестность начала координат, причем бук-
вы соответствуют обозначениям на рис. 122. Ударная волна изо-
бражается в плоскости годографа не одной линией, а двумя (со-
ответствующими движению газа по
^вй обеим сторонам разрыва), причем

И

области между ними (заштрихован-
ной на рис. 123) не соответствуют
F никакой области в физической пло-
скости.
Прежде всего необходимо выяс-
^ нить, какой из общих интегралов Ф_й
соответствует данному случаю об-
F' текания. Если Ф(0, и) имеет поря-
док однородности k, то функции
, х = дФ/дц и у = дФ/dQ будут одно-
родными — соответственно порядков
Рис. 123 k — 1/3 и k — 1/2. При стремлении 8

и и к нулю мы должны, вообще говоря, попасть на бесконечность в физической плоскости, т. е. х и у должны стремиться к бесконечности. Очевидно, что для этого должно быть k < 1/3. С другой стороны, предельные ха­рактеристики в физической плоскости не должны лежать цели­ком на бесконечности, т. е. не должно быть у = ±оо по всей линии 98² = 4т1³. Для этого (при 2k + 1/6 < 5/6) второй член в квадратных скобках в выражении (118,6) должен вообще от­сутствовать. Таким образом, функция Ф(8, г)) должна изобра­жаться первым членом выражения (118,6):

Ф = Л9²*P(-k, -k + -2Л + |-; 1-Ц-). (120,1)

Функция |/(в, rj) (тоже удовлетворяющая уравнению Эйлера — Трикоми) будет иметь такой же вид с & — '/г вместо k.

Но если выражение (120,1) имеет место, например, вблизи верхней характеристики (0 = -f²/зЛ^3/2), то при произвольном k < Уз оно отнюдь не будет иметь место также и вблизи второй характеристики (0 = —²/зц³''²). Поэтому мы должны потребо­вать также, чтобы вид (120,1) функции Ф(0, ц) оставался таким же при обходе вокруг начала координат в плоскости годографа от одной характеристики к другой, причем обход должен про­исходить через полуплоскость ц < 0 (путь А'В' на рис. 119). Такой обход соответствует в физической плоскости переходу от удаленных точек одной из предельных характеристик к удален­ным точкам другой предельной характеристики, причем путь перехода проходит через дозвуковую область и потому нигде не пересекает ударную волну, нарушающую непрерывность тече­ния. Преобразование гипергеометрической функции в (120,1) при таком переходе дается первой из формул (118,13), и мы должны потребовать обращения в нуль коэффициента перед F₂ в этой формуле. Это условие выполняется при следующих значениях k < Уз:

* = 4 — у, п = 0, 1, 2,...

Из всех этих значений должно быть окончательно выбрано лишь одно:

k = -j. (120,2)

Можно показать, что все значения k с п > 1 приводят к неод­нозначному отображению плоскости годографа на физическую плоскость (при однократном обходе первой вторая обходится несколько раз), т. е. к неоднозначности физического течения, что, разумеется, нелепо. Значение же £='/б дает решение, в ко­тором не по всем направлениям в физической плоскости стрем­ление 9 и г| к нулю означает уход на бесконечность; ясно, что такое решение тоже физически непригодно.

При k = —Уз коэффициент при F\ в правой стороне фор­мулы (118,13) равен +1, т. е. при обходе от одной характери­стики к другой функция Ф вообще не меняется. Это значит, что Ф есть четная функция 0, а координата у = дФ/дВ— соот­ветственно нечетная функция. Физически это означает, что в рассматриваемом нами первом приближении картина течения на больших расстояниях от тела оказывается симметричной относи­тельно плоскости у = 0 независимо от формы тела, в частности от наличия или отсутствия подъемной силы.

Таким образом, мы выяснили характер особенности, которую имеет Ф(т], 0) в точке г| = 0 = О. Уже непосредственно отсюда можно сделать заключение о форме звуковой линии, предельных характеристик и ударной волны на больших расстояниях от тела. Каждая из этих линий должна соответствовать определен­ному значению отношения в²/¹!³» ^и поскольку Ф имеет вид ф = 0-²/з/(т|³/0²), то с помощью формул (118,4) мы найдем, что х оо 9^-4/3, у со 0-⁵/³. Поэтому форма перечисленных линий опре­деляется уравнениями вида

Jc = const-«/⁴'⁵ (120,3)

со своим значением const для каждой из них. Вдоль этих линий бит) падают по законам:

9оо^-з.'5, _л 00^-2/5 (120,4)

(Ф. И. Франкль, 1947; К. Guderley, 1948) •).

Мы будем для определенности писать формулы со знаками, соответствующими верхней полуплоскости (г/>0).

Покажем, как могут быть вычислены коэффициенты в этих формулах. Значение k = —'/з есть одно из тех, при которых Ф<> сводится к алгебраическим функциям (см. предыдущий па­раграф). Тот частный интеграл, который в данном случае опре­деляет Ф, может быть написан в виде Ф = -тг -Ц-. где а\ —

произвольная положительная постоянная, а / есть тот корень кубического уравнения

/³-3r)f + 30 = 0, (120,5)

который при 90² — 4г|³ > 0 совпадает с единственным веществен­ным корнем. Отсюда

ф ₌ ^1^₌ £i (120 6>

2 ае 2(Р-т))' и^,о/

а также для координат

^Х~~ <?т] ~~ 2(/²-T|)^J ' ^y— сЮ ^— (Р-т))³ ' ^^1ZU'''

Эти формулы можно представить в удобном параметрическом виде, введя в качестве параметра величину s — f²/(f²— п); тогда

y Ос 1

^=< -^г; w^2/5 = ^а?*^т (^s ~¹)• = -у- «^4/5(3-2_S),

(120,8)

⁴) Упомянем, что аналогичные результаты оказывается возможным полу­чить и для осесимметричного обтекания (с Moo = 1). В цилиндрических кординатах х, г форма звуковой поверхности, предель­ной характеристики и ударной волны, и законы изменения скорости на них даются (вдали от тела) формулами х — const • л⁴'⁷, Идоо/-^-6'⁷, v_roor~⁹¹⁷. См. Гудерлей К- Г. Теория околозвуковых течений. — М.: ИЛ, 1960 \Guder- ley К- G. Theorie schallnaher Stromungen.— Springer Verlag, 1957]; Фалько-вич С. В., Чернов И. А. — Прикл. Матем. Мех., 1964, т. 28, с. 342.

чем определяется в параметрическом виде зависимость п и 0 от координат. Параметр s пробегает положительные значения, на­чиная от нуля (s = 0 соответствует х — —со, т. е. натекающему с бесконечности потоку). В частности, значение s = '/₂ соответ­ствует х = 0, т. е. дает распределение скоростей при больших у в перпендикулярной к оси х плоскости, проходящей в районе об­текаемого тела. Значение s = 1 соответствует звуковой линии (т] = 0), a s = ⁴/₃, как легко убедиться, — предельной характе­ристике. Значение же постог.аной ai зависит от конкретной фор­мы обтекаемого тела и могло бы быть определено лишь путем точного решения задачи во всем пространстве.

Формулы (120,8) относятся лишь ко всей области перед удар­ной волной. Неизбежность появления последней видна уже из следующих соображений. Простое вычисление по формуле (118,5) дает для якобиана А выражение

¹ (/² - ч)³ '

Легко видеть, что на характеристиках и во всей области слева от них (что соответствует области вверх по течению от предель­ных характеристик в физической плоскости) А > 0 и нигде в нуль не обращается. В области же справа от характеристик А проходит через нуль, откуда и видна неизбежность возникнове­ния здесь ударной волны.

Граничные условия, которым должно удовлетворять решение уравнения Эйлера — Трикоми на ударной волне, заключаются в следующем. Пусть 0i, х\\ и 6₂, Пг — значения 0 и и по обеим сто­ронам разрыва. Прежде всего они должны соответствовать од­ной и той же кривой в физической плоскости, т. е.

х(9„ ч.) = ^(02. %). у$1* Ч1) = 0(в»ДЬ)- (120,9)

Далее, условие непрерывности касательной к разрыву компо­ненты скорости (т. е, условие непрерывности производной от по­тенциала ф вдоль линии разрыва) эквивалентно условию непре­рывности самого потенциала:

<Р(еьЛ1) = ф(в₂,ч₂) (120,10)

(потенциал ф определяется по функции Ф формулой (119,3)). Наконец, последнее условие можно получить из предельной формы уравнения ударной поляры (92,6), устанавливающего определенную связь между компонентами скорости по обеим сторонам разрыва. Заменив в (92,6) угол / на 0₂ — 0i и введя г)1, т)₂ вместо v\, vi, получим следующее соотношение:

2(6₂-е₁)² = (Л2-тц)²(т12 + Л1). (120,11)

В данном случае решение уравнения Эйлера — Трикоми по­зади ударной волны (область между OF и OF' в плоскости го­дографа; рис. 123) имеет тот же вид (120,5—6), ио, конечно, с другим постоянным коэффициентом (обозначим его как —а₂) вместо аь Четыре уравнения (120,9—11) определяют отношение a₂/ai и связывают между собой величины: rji. вь 42, 6₂. В резуль­тате довольно сложного их совместного решения получаются следующие результаты. Ударной волне соответствует значение

s = (5 л/3+ 8)/б = 2,58

параметра s в формулах (120,8), дающих при этом форму волны и распределение скорости на передней стороне разрыва. В об­ласти позади (вниз по течению) от ударной волны коэффициент —а₂ оказывается отрицательным, а параметр f²/(f² — и) пробегает отрицательные значения. Вводя

здесь в качестве s положитель­на

ную величину s = ц — р> получим вместо (120,8) формулы

а³'⁵

Qysis ₌---------- 2__s4/5(_2s + 3)_> (120,12)

причем

ajai = (9 V3 + 0/(9 Уз - l) =

= 1,14,

a s пробегает значения от

_S = (5V3 — 8)/6 = 0,11

(на ударной волне) до нуля (на
бесконечности вниз по течению).
Рис. 124 На рис. 124 изображены гра-

фики зависимости цу^2,ъ и 9г/^3/5 от jq/-⁴/⁵, вычисленные по формулам (120,8) и (120,12) (постоянная «1 условно положена равной единице).

§ 121. Отражение слабого разрыва от звуковой линии

Рассмотрим, снова с помощью уравнения Эйлера — Трикоми, отражение слабого разрыва от звуковой линии.

Будем считать, что падающий на звуковую линию слабый разрыв («приходящий» по отношению к точке их пересечения) — обычного типа, возникающего, скажем, при обтекании острых

углов, т. е. разрыв первых производных скорости по координа­там. Он отражается от звуковой линии в виде другого разрыва, характер которого, однако, заранее неизвестен и должен быть определен путем исследования течения в окрестности точки пе­ресечения. Последнюю выбираем ниже в качестве начала коор­динат х, у, а ось х — вдоль направления скорости газа в этой точке; тогда ей соответствует начало координат и в плоскости годографа.

Слабые разрывы расположены, как мы знаем, вдоль харак­теристик. Пусть приходящему разрыву соответствует в пло-

У /а

/

/

----- 4

а)

- Слабый разрыв ■ Звуковая линия.

б)

h

А г I \

d 'а ' С

Рис. 125

скости годографа характеристика Оа (рис. 125,а). Непрерыв­ность координат х, у на разрыве означает, что должны быть непрерывными первые производные Ф„, Фе. Напротив, вторые производные от Ф -выражаются через первые производные от скорости по координатам и потому должны испытывать разрыв. Обозначая скачки величин квадратными скобками, имеем, таким образом: на Оа:

[<ГУ = [Фе] = 0; [Фее], [Ф_вчЬ [Ф J Ф 0. (121,1)

Сами же функции Ф в областях / и 2 по обе стороны от харак­теристики Оа не должны иметь на ней никаких особенностей. Та­кое решение можно построить с помощью второго члена в (118,6) с k —11/12, пропорционального квадрату разности (1—4г)³/90²) (второе же независимое решение Фц/12 имеет на характеристике особенность — см. ниже); первые производные этой функции на характеристике обращаются в нуль, а вто­рые — конечны. Кроме того, в Ф могут войти такие частные ре­шения уравнения Эйлера — Трикоми, которые не приводят ни к каким особенностям течения в физической плоскости. Наиболее низким по степеням Э и п таким решением является От) (§ 119). Таким образом, вблизи характеристики Оа ищем Ф в виде

Ф_а1 = -Л_ч9-^'^(-|,

o_a2 = -^e-ceⁿ'⁶6²F(|-, -Ц.

3; |). 3; б).

(121,2)

где индексы а\ и а2 указывают окрестности по обе стороны ха­рактеристики (в областях / и 2); А, В, С — постоянные, и снова введено обозначение

t ₌ l _i!!L

(на характеристике | = 0).

Мы увидим ниже, что в зависимости от знака произведения АВ могут иметь место два случая: слабый разрыв отражается в виде слабого же разрыва другого (логарифмического) харак­тера или в виде ударной волны малой интенсивности.

Отражение в виде слабого разрыва

Рассмотрим сначала первый из этих случаев (Л. Д. Ландау, Е. М. Лифшиц, 1954). Отраженному от звуковой линии слабому разрыву соответствует в плоскости годографа вторая характе­ристика (Ob на рис. 125,а). Вид функции Ф вблизи этой харак­теристики устанавливается путем аналитического продолжения функций (121,2) согласно формулам (118,11—13). Однако при 11/12 функция F\ теряет смысл и поэтому непосредственно воспользоваться этими формулами нельзя. Вместо этого надо положить в них сначала &= 11/12+ е, после чего устремить в к нулю. В соответствии с общей теорией гипергеометрического уравнения при этом появляются логарифмические члены.

В результате вычисления (с помощью (118,13)) для функции Ф вблизи характеристики Ob в области 3 получается следующее выражение (с точностью до членов второго порядка по \ вклю­чительно):

Ф_Ьз = - Л0г, + £(- 0)^и/б a² InШ + с₀ + с,Е + с₂|²}, (121,3)

* где Со, Си С2 — числовые постоянные¹). Аналогичное преобразо­вание (с помощью (118,11)) функции Фаг от окрестности харак­теристики Оа к окрестности характеристики Ob дает функцию Ф_Ь2, отличающуюся от (121,3) лишь заменой В на С/2. Коорди­наты х, у точек характеристики в физической плоскости вычис-

) Значение этих постоянных:

с„ = -2⁹ • 3⁴/385 = - 108, с, = 288/7 = 41,1, с₂ = 4,86.

ляются как производные (118,4), взятые при £ = 0. Так, исходя из (121,3) найдем

*₌_ле--!^(-еГ,

* (121,4)

. (39 \^2/3 В (11, с, \, ыЫб

а дифференцирование функции Фь₂ даст такие же выражения с С/2 вместо В. Условие непрерывности координат х, у на ха­рактеристике Ob приводит, следовательно, к соотношению

С = 2В. (121,5)

Далее, для осуществления рассматриваемой картины отраже­ния должны отсутствовать предельные линии в плоскости годо­графа (и тем самым — нефизические области в этой плоскости), т. е. якобиан Д нигде не должен проходить через нуль. Вблизи характеристики Оа якобиан вычисляется с помощью функций

(121.2) и оказывается положительным (главный член в нем: Д «Л²). Вблизи же характеристики Ob вычисление с помощью

(121.3) дает

Д ~ А² - 16 (|)"⁶ ЛЯГ,"⁴ In. (121,6)

При приближении к характеристике логарифм стремится к —с», и главным является второй член. Поэтому из условия Д > 0 имеем А В > 0, т. е. А и В должны иметь одинаковый знак.

Наконец, для определения формы звуковой линии нам пона­добятся выражения для Ф вблизи оси ц = 0. Выражение, при­годное в окрестности верхней части этой оси, получается просто преобразованием гипергеометрической функции в Ф (121,2) в гипергеометрические функции аргумента 1 —- g = 4r)^s/98², обра­щающегося в нуль при п^О¹). Сохранив лишь члены наиболее низких степеней по г\, получим

Ф_а=-Атф-_r(23/²f₂₎⁽ffi_17/12)Д9"^/6=-Лг|8-б',25В8"^/6- (121,7)

Аналитическое же продолжение в область нижней части оси дает

Ф_с=- Лг,8 — 6,25- УзВ8^11/6 (121,8)

(вычисления аналогичны выводу формулы преобразования (118,13)).

Теперь можно определить форму всех интересующих нас ли­ний. На характеристиках имеем, отбрасывая члены более высо-

*) Это преобразование приведено, например, в § е Математического при­ложения в III — формула (е, 7).

кого порядка: # =—Л0, у = —Лт]. Мы условились считать, что приходящему слабому разрыву отвечает верхняя характеристика (6 >0). Поскольку скорость газа направлена в положительном направлении оси х, то этот разрыв, для того чтобы быть прихо­дящим, должен лежать в полуплоскости х <с 0. Отсюда следует, что постоянная Л, а с нею и В должны быть положительными. Уравнение линии слабого разрыва в физической плоскости будет

_у = (|)^2/3Л^1/3(-х)^2/3=1,31Л^1/3(-_Л)^2/3. (121,9)

Отраженный же разрыв, соответствующий нижней характери­стике, дается уравнением')

-#=1,31Л^1/Зл:^2/3 (121,10)

(см. рис. 125,6; обозначение линий и областей на этом рисунке Соответствует обозначениям на рис. 125, а).

Уравнение звуковой линии получается из функций (121,7—8). Дифференцируя по ц и 0 и положив затем г\ = 0, получим из (121,7) уравнение той части линии, на которой 0 > 0:

х = -Л0, у = — Л.. 6,25В0^г,/6,

откуда

y=-UABA-^5l6(- xf\ (121,11)

Это — нижняя часть звуковой линии на рис. 125,6. Аналогич­ным образом из (121,8) находим уравнение верхней части этой линии:

0 = 11,4УЗ ВА-^ътх^ъ'\ (121,12)

Таким образом, оба слабых разрыва и обе ветви звуковой ли­нии имеют в точке пересечения О общую касательную (ось у), причем две ветви звуковой линии лежат по разные стороны оси у.

На приходящем разрыве испытывают скачок производные от скорости по координатам. В качестве характерной величины рас­смотрим скачок'производной (дг\/дх)_у. Имея в виду, что

(дх\ \ _ д(т|, у) ^ <?(т|, у), д(х, у) 1 <?^гФ

\дх)_у д (х, у) д (г), в) / д (т), 6) Д 39²

и воспользовавшись формулами (121,2), (121,5), получим для искомого скачка:

При приближении к точке пересечения он растет как (—#)^-1/4.

') С учетом первых поправочных членов (вторые члены в формулах (121,4)) уравнение отраженного разрыва:

- у = 1.31А¹ V³ - Ю,58Л -^5/V⁵. (121, 10а)

На отраженном же слабом разрыве производные скорости вообще не испытывают скачка, но распределение скоростей имеет своеобразную логарифмическую особенность. Вычислив из функ­ции (121,3) (сохранив в ней лишь первый член в скобках) ко­ординаты х и у в функции от tj, 0, можно представить зависи­мость ц от х при заданном у вблизи отраженного разрыва в следующем параметрическом виде:

т/. (121,14)

_ц = Ш- + -Л^-^1у^ А 1 -у А \у\ 6Л

где £ играет роль параметра, а Хо = хо(у)— уравнение линии разрыва в физической плоскости.

Отражение в виде ударной волны

Перейдем к рассмотрению другого случая — отражения сла­бого разрыва от звуковой линии в виде ударной волны (Л. П. Горькое, Л. П. Питаевский, 1962)').

e+ fn^3/2

е=^т~т- 021,15)

Этот случай возникает, если произведение АВ < 0. Из (121,6) видно, что в этом случае имеется две предельные линии, экспо­ненциально близкие к характеристике Ob: якобиан А обращается в нуль при

Ля (2/3)^1/6 16|В|ч

¹⁶¹ Ю1

Заранее очевидно, что экспоненциально близкими к характери­стике будут и границы нефизической области на плоскости годо­графа (Obi и ОЬг на рис. 126,а), и тем самым будет экспонен­циально мала интенсивность ударной волны.

Пренебрегая экспоненциально малыми значениями £ на ли­ниях ОЬ₂ и ОЬ₃, мы получим для координат х, у на них те же выражения, которые мы имели на двух сторонах характеристики Ob в предыдущем случае. Поэтому условие непрерывности коор­динат на ударной волне во всяком случае приводит к прежнему соотношению (121,5). Соответственно, остается прежним и выра­жение (121,13) для скачка производной от скорости на падаю­щем разрыве. Снова приняв, что этому разрыву отвечает верхняя характеристика Оа на плоскости годографа, будем по-прежнему иметь А > 0, так что теперь В < 0. Из (121,13) видно, следо­вательно, что физическим критерием происхождения двух слу-

') Принципиальная возможность такого отражения отмечалась ранее Г у* дерлеем (К. G. Guderley, 1948).

чаев отражения слабого разрыва является знак скачка произ­водной скорости на падающем разрыве.

Остаются прежними (при пренебрежении экспоненциально малыми поправками) уравнения (121,9—10) линий падающего (слабого) и отраженного (ударной волны) разрывов. Но ввиду другого знака постоянной В меняется расположение этих линий на физической плоскости — как это показано на рис. 126,6.

В

Рис. 126

Для определения интенсивности ударной волны (т. е. скач­ков величин 68 и 8ц на ней) надо обратиться к полной системе граничных условий, которым должно удовлетворять на ударной волне решение уравнения Эйлера — Трикоми. Они были сформу­лированы уже в § 120: условия (120,9—11). Из них последнее, уравнение ударной поляры, принимает вид (68)² = т](6г|)², где 69 = 062 — 0»з, 6rj = Г|62 — Цьз — экспоненциально малые скачки величин на ударной волне (индексы 62 и &3 относятся к линиям ОЬг и 06₃ на плоскости годографа, т. е. соответственно к перед­ней и задней сторонам ударной волны на физической плоскости). Отсюда

60 = Ул6г,; (121,16)

выбор знака при извлечении корня определяется тем, что одно­временно с уменьшением скорости газа при его прохождении через ударную волну должно происходить приближение линий тока к поверхности разрыва.

В соответствии с (121,15) ищем уравнения линий 06₂ и ОЬз в плоскости годографа в виде

6 + 1 ту³/² = a_b2101 е-», 0 + 4 г,^,/2 = - %> 19 |в-в

где а — (аь2 + а_Ьъ)/2; переменные п, 9 выражены через коорди­наты на физической плоскости согласно х «—Л9, у» —Ац. Определение коэффициента а требует учета также и всех осталь­ных граничных условий, причем в них должны учитываться чле­ны как линейные, так и квадратичные по экспоненциально ма­лой величине ехр(—в). Не приводя этих довольно громоздких вычислений, укажем лишь их результат: а&₂ = «бз — а = 5,2,

ГЛАВА XIII

ОБТЕКАНИЕ КОНЕЧНЫХ ТЕЛ

§ 122. Образование ударных воли при сверхзвуковом обтекании тел

Простые соображения показывают, что при обтекании про­извольного тела сверхзвуковым потоком перед телом возникает ударная волна. Действительно, в сверхзвуковом потоке возмуще­ния, обусловленные наличием обтекаемого тела, распростра­няются только вниз по течению. Поэтому натекающий на тело однородный сверхзвуковой поток должен был бы доходить до самого переднего конца тела невозмущенным. Но тогда на по­верхности этого конца нормальная компонента скорости газа была бы отличной от нуля в противоречии с необходимым гра­ничным условием. Выходом из этого положения может являться только возникновение ударной волны, в результате чего движе­ние газа между нею и передним кон­цом тела становится дозвуковым.

Рис. 127

Таким образом, при сверхзвуковом обтекании тела перед ним возникает ударная волна; ее называют головной. При обтекании тела с тупым перед­ним концом эта волна не соприкасает­ся с самим телом. Спереди от ударной волны поток однороден, а позади нее движение меняется, и поток огибает обтекаемое тело (рис. 127,а). Поверх­ность ударной волны уходит на беско­нечность, причем вдали от тела, где интенсивность волны мала, она пересекает направление набегающего потока под углом, близким к углу Маха. Характерной чертой обтекания тела с ту­пым концом является существование дозвуковой области течения за ударной волной — позади наиболее выдающейся вперед части ее поверхности; эта область простирается до обтекаемого тела и, таким образом, ограничена поверхностью разрыва, поверх­ностью тела и «боковой» звуковой поверхностью (пунктирные линии на рис. 127,а).

Дата добавления: 2014-11-07