Должно быть 7 страница

') В рассматриваемом приближении конус х = fir представляет собой поверхность слабого разрыва. В следующем приближении появляется ударная волна, интенсивность которой (относительный скачок давления) пропорцио­нальна %*, а угол полураствора превосходит угол Маха на величину, тоже пропорциональную х*.

ГЛАВА XII

ПЛОСКОЕ ТЕЧЕНИЕ СЖИМАЕМОГО ГАЗА

§ 114. Потенциальное движение сжимаемого газа

Мы встретимся в дальнейшем с многочисленными важными случаями, когда движение сжимаемого газа можно рассмат­ривать как потенциальное практически во всем пространстве. Здесь мы выведем общие уравнения потенциального течения и рассмотрим в общем виде вопрос об их применимости¹).

Потенциальность течения сжимаемого газа нарушается, во­обще говоря, ударными волнами; после прохождения через удар­ную волну потенциальный поток становится в общем случае вих­ревым. Исключение представляют, однако, случаи, когда стацио­нарный потенциальный поток проходит через ударную волну постоянной (вдоль всей ее поверхности) интенсивности; таковы, например, случаи, когда однородный поток проходит волну, пе­ресекающую все линии тока под одинаковым углом²). В таких случаях течение остается потенциальным и позади ударной волны.

Для доказательства этого утверждения воспользуемся урав­нением Эйлера, написанным в виде

yVo² — [v rotv]= — — Vp

(ср. (2.10)), или

где учтено термодинамическое соотношение dw = Т ds -j- dp/P-Но в потенциальном потоке перед ударной волной w + v²/2 — = const, а на ударной волне эта величина непрерывна; поэтому она останется постоянной и во всем пространстве позади удар­ной волны, так что будем иметь:

[v rot v] = — TVs.

(114.1 >

') В этом параграфе течение еще не предполагается плоским! ²) С такими случаями мы уже встречались при изучении сверхзвукового» обтекания клина и конуса (§§ 112, 113).

Потенциальный поток перед ударной волной изэнтропичен. В общем случае произвольной ударной волны с переменным вдоль ее поверхности скачком энтропии в пространстве за вол­ной градиент Vs ф 0, а вместе с ним будет отличен от нуля и rotv. Однако если ударная волна обладает постоянной интен­сивностью, то и скачок энтропии в ней постоянен, так что тече­ние за ней тоже будет изэнтропическим, т. е. Vs — 0. Отсюда следует, что либо rot v = 0, либо векторы rot v и v везде парал­лельны друг другу. Но последний случай невозможен: на самой ударной волне v во всяком случае имеет отличную от нуля нор­мальную компоненту, а нормальная компонента rot v во всяком случае равна нулю (нормальная компонента rotv определяется тангенциальными производными от тангенциальных компонент скорости, непрерывных на поверхности разрыва).

Другой важный случай, когда потенциальность течения мож­но считать не нарушающейся ударными волнами, — это случай волн малой интенсивности. Мы видели (§ 86), что в таких удар­ных волнах скачок энтропии есть величина третьего порядка по сравнению со скачком давления или скорости. Из соотношения (114,1) видно поэтому, что величиной третьего порядка будет и rotv за разрывом. Это и дает возможность считать, с точ­ностью до малых величин высших порядков, течение потенциаль­ным и позади ударной волны.

Выведем общее уравнение для потенциала скорости при про­извольном стационарном потенциальном течении сжимаемого газа. Для этого исключаем плотность из уравнения непрерыв­ности divpv = р div v -j- v Vp — 0 с помощью уравнения Эйлера

ч Vp с²

_{(vv)v =} JL^.—yp

и получаем:

с² div v — (W) v = 0.

Вводя сюда потенциал согласно v = V(p и раскрывая векторные выражения, найдем искомое уравнение:

(с² - ф²) <р_хх + (с² - ф²) ср_уу + (с* - ф²) _Фгг -

— 2 (фяф^ф^ + ФхФгФяг + фуФгФуг) = 0 (114,2)

(нижние индексы обозначают здесь частные производные). В частности, для плоского движения

(с°' - Ф„ + (*² - Ф %_у ~ 2<адур_х, = 0. (114,3)

В этих уравнениях скорость звука сама должна быть выражена как функция скорости, что может быть, в принципе, сделано с помощью уравнения Бернулли w -j- v²/2 = const и уравнения изэнтропичности s = const (для политропного газа зависимость с от v дается формулой (83,18)).

Уравнение (114,2) очень упрощается, если во всем простран-•стве скорость газа лишь незначительно отличается по величине и направлению от скорости натекающего из бесконечности по­тока¹). Тем самым подразумевается и что ударные волны (если они вообще есть) обладают слабой интенсивностью, а потому не нарушают потенциальности течения.

Выделим из v постоянную скорость натекающего потока vi, написав v = vi-f-v^/, где v' — малая величина. Вместо потен­циала ф полной скорости, введем потенциал ф' скорости v': у' = Уф'. Уравнение для этого потенциала получится из (114,2) заменой ф = ф' + xv\ (ось х выбираем в направлении век­тора vi). Рассматривая после этого ф' как малую величину и опуская все члены выше первого порядка, получим следующее линейное уравнение:

O-MD^ + ^ + lS—O, (П4,4>

где Mi = V\/c\\ для скорости звука здесь подставлено, естествен­но, ее заданное значение на бесконечности.

Давление в любой точке потока определяется в этом же приближении через скорость по формуле, которую можно по­лучить следующим образом. Рассматривая р как функцию w (при заданном s) и учитывая, что (dw/dp)_s = 1/р, пишем:

P — Pi** {lw~)_s ^ ~ ^w^ ^{= р1} (^ш ~~ Согласно же уравнению Бернулли имеем:

^w- щ = -1[(^vi + ^v)²-^у?] ~ -т(°5 + ^VD - °»°*•

так что

p-p_x = -_9xv_xv_x--^{vl + vD. (114,5)

В этом выражении надо, вообще говоря, сохранить член с квад­ратами поперечной скорости, так как в области вблизи оси х (в частности, на самой поверхности обтекаемого газом тонкого тела) производные ду'/ду, ду'/dz могут стать большими по сравнению с дхр'/дх.

⁴) С таким случаем мы встретились уже в § 113 (обтекание тонкого ко­нуса) и встретимся еще при изучении обтекания сжимаемым газом произволь­ных тонких тел.

Уравнение (114,4), однако, неприменимо, если число Mi очень близко к единице (околозвуковое движение), так что коэффи­циент в первом члене становится малым. Ясно, что в таком слу­чае в уравнении должны быть сохранены также и члены более высокого порядка по производным потенциала по координате х. Для вывода соответствующего уравнения снова вернемся к исходному уравнению (114,2), которое после пренебрежения заведомо малыми членами сводится к следующему:

(l —-$•) Ф** + 4W + Фя == 0. (114,6)

В рассматриваемом случае скорость»,«с и скорость звука с близки к критической скорости с*. Поэтому можно написать:

с — c. — (v — С) -г— * ^v *' dv

или

c — v = (c—v)(l—-£-\ У ^v * ' \ dv \₀*.cJ

Воспользовавшись тем, что при v = с — с* согласно (83,4) имеем dp/dv = —р/с, пишем (при v = с*):

dcdc dp р dc

dv dp dv с dp

так что

_c_₀ = (_Ce_₀)liM. = a.(c.-«). (114,7)

Мы воспользовались здесь для производной d(pc)/dp выраже­нием (99,9), а а* обозначает значение величины а (102,2) при и = с* (для политропного газа а есть просто постоянная, так что а* = <х = (у+ 1)/2). С той же точностью это равенство можно переписать в виде

y-l=«.(t-l). (114,8)

Это соотношение устанавливает в общем виде связь между чис­лами М и М„в околозвуковом случае. С помощью этой формулы пишем:

v⁷' V² (V \ г V \

Наконец, вводим новый потенциал, производя замену

ф ->- С, (X + ф),

так что теперь будет

дф v_x (Эф v_u дф v.

-г- = —-1. = —. 1Г-=* — - (П4,9)

дх с, ' ду с, dz с, \ > /

Внося все это в (114,6), получим окончательно следующее урав­нение для потенциала околозвукового течения (с направлением скорости, везде близким к оси х):

dv d²w d'tr. d²a>

Свойства газа входят сюда только через постоянную а*. Мы увидим в дальнейшем, что зависимость всех вообще свойств околозвукового течения от конкретного рода газа целиком опре­деляется этой постоянной.

Линеаризованное уравнение (114,4) становится непримени­мым и в другом предельном случае — очень больших значений Mi, не говоря уже о том, что благодаря возникновению сильных ударных волн реальное течение при таких Mi фактически вообще нельзя считать потенциальным (см. § 127).

§ 115. Стационарные простые волны

Определим общий вид решений уравнений стационарного плоского сверхзвукового движения газа, описывающих течения, при которых на бесконечности имеется однородный плоско-па­раллельный поток, в дальнейшем своем течении поворачиваю­щий, обтекая искривленный профиль. С частным случаем такого решения нам уже приходилось иметь дело при изучении движе­ния вблизи угла, — при этом мы по существу рассматривали плоско-параллельный поток, текущий вдоль одной из сторон угла и поворачивающий вокруг края этого угла. В этом частном ре­шении все величины — две компоненты скорости, давление, плот­ность— были функциями всего лишь от одной переменной — от угла ср. Поэтому каждая из этих величин могла бы быть выра­жена в виде функции одной из них. Поскольку это решение должно содержаться в виде частного случая в искомом общем решении, то естественно искать это последнее, исходя из требо­вания, чтобы и в нем каждая из величин р, р, v_x, v_y (плоскость движения выбираем в качестве плоскости х, у) могла быть вы­ражена в виде функции одной из них. Такое требование пред­ставляет собой, конечно, весьма существенное ограничение, на­лагаемое на решение уравнений движения, и получающееся та­ким образом решение отнюдь не является общим интегралом этих уравнений. В общем случае каждая из величин p, р, v_x, v_y» являющихся функцией двух координат х, у, могла бы быть вы­ражена лишь через две из них.

Поскольку на бесконечности имеется однородный поток, в ко­тором все величины, в частности и энтропия s, постоянны; а при стационарном движении идеальной жидкости энтропия сохра­няется вдоль линий тока, то ясно, что и во всем пространстве будет s = const, если только в газе нет ударных волн, что и предполагается ниже.

Уравнения Эйлера и уравнение непрерывности имеют вид

dv_x dv, 1 dp dv_y dv_y 1 dp

^Vx~dT ^JtVy~dy~^~~9~dx- ^V% ~dx"^ ^иУ ~dy~ ~ ~~ VW'

■|r(P^o*) + -^-(PO,) = 0,

Написав частные производные в виде якобианов, переписываем эти уравнения в виде

д (v_x, у) д (v_x, х) 1 а (р, у)

- --------- v„ —

д(х, у) у д(х, у) о д(х, у) '

д (v_y, у) д (v_y, X) _ 1 д (р, х)

= 0.

а {х, у) у д(х,_У) р а (х, у) ^д (Р°х> У) ^д (PV ^х)

а (х, у) а (х, у)

Выберем теперь в качестве независимых переменных х и р. Для того чтобы произвести соответствующее преобразование, доста­точно умножить написанные уравнения на д (х, у) /д (х, р), в ре­зультате чего получим уравнения в точности того же вида, с той лишь разницей, что в знаменателях всех якобианов будет стоять д(х, р) вместо д(х,у). Раскроем эти якобианы; при этом надо иметь в виду, что в независимых переменных х и р все вели­чины р, v_x, v_y являются, по предположению, функциями только от р, и потому их частные производные по х равны нулю. Тогда получаем:

(_ ^dv* — ^{1 ду} (_ ^ду \ ^dvy _ ¹

\^Vy ^V* дх) dp р дх ' \^Vy ^V* дх) dp ~ р '

(ay\dp (dv ду dv_x\

(где ду/дх обозначает (ду/дх)_р). Все величины в этих уравне­ниях, за исключением лишь ду/дх, являются функциями только от р уже по сделанному предположению, а х вовсе не входит в уравнения явным образом. Поэтому прежде всего можно за­ключить на основании этих уравнений, что и ду/дх есть некото­рая функция только от р:

(£),-'.«■

откуда

y = xf_l(p) + f₂(p), (115,1)

Где \₂(Р) — произвольная функциядавления.

Дальнейших вычислений можно не производить вовсе, если непосредственно воспользоваться известным уже нам частным решением для волны разрежения при обтекании угла (§§ 109,112). Напомним, что в этом решении все величины (в том числе и давление) постоянны вдоль каждой прямой (характеристики), проходящей через вершину угла. Это частное решение, очевидно, соответствует случаю, когда в общем выражении (115,1) произ­вольная функция fz(p) тождественно равна нулю. Функция же fi(p) определяется полученными в § 109 формулами.

Уравнение (115,1) при постоянных значениях р определяет семейство прямых линий в плоскости х, у. Эти прямые пересе­кают в каждой своей точке линии тока под углом Маха. Это оче­видно из того, что таким свойством обладают прямые у = xfi (р) в частном решении с /г = 0. Таким образом, и в общем случае одно из семейств характеристик (характеристики, «исходящие» от поверхности тела) представляет собой прямые лучи, вдоль ко­торых все величины остаются постоянными; эти прямые, однако, не имеют теперь общей точки пересечения.

Изложенные свойства рассматриваемого движения в матема­тическом отношении полностью аналогичны свойствам одномер­ных простых волн, у которых одно из семейств характеристик представляет собой семейство прямых линий в плоскости х, t (см. §§ 101, 103, 104). Поэтому рассматриваемый класс течений играет в теории стационарного плоского (сверхзвукового) дви­жения такую же роль, какую играют простые волны в теории нестационарного одномерного движения. Ввиду этой аналогии эти течения тоже называют простыми волнами. В частности, волну разрежения, соответствующую случаю f₂ s= 0, называют центрированной простой волной.

Как и в нестационарном случае, одно из важнейших свойств стационарных простых волн заключается в том, что течение во всякой области плоскости х, у, граничащей с областью однород­ного потока, есть простая волна (ср. § 104).

Покажем теперь, каким образом может быть построена про­стая волна для обтекания заданного профиля.

На рис. 115 изображен обтекаемый профиль; слева от точки О он прямолинеен, далее от точки О начинается закругление. В сверхзвуковом потоке влияние закругления распространяется, разумеется, лишь на область потока вниз по течению от исхо­дящей из точки О характеристики OA. Поэтому все течение сле­ва от этой характеристики будет представлять собой однород­ный поток (относящиеся к нему значения величин отличаем ин­дексом 1). Все характеристики в этой области параллельны друг другу и наклонены к оси х под углом Маха ai = arcsin(ci/ui).

В формулах (109,12—15) угол наклона характеристик ф от-считывается от луча, на котором v = с = с*. Это значит (ср. § 112), что характеристике OA надо приписать значение угла ф, равное

Ф1= V"Y^T^arCC°^S~S"'

и в дальнейшем отсчитывать углы ф для всех характеристик от направления OA' (рис. 115). Угол наклона характеристик к оси х будет тогда равен Ф* —Ф, где q>* = ai + фь Согласно форму­лам (109,12—15) скорость и давление выразятся через угол ф посредством

1^ = 11 cos 9, Vy = vsinQ, (115,2)

*=*: [ 1+^sin2 Viff ф] • t¹¹⁵>з)

е = ф,-ф-агс!_§(д/^|ctg д/^|ф), (115,4)

Р = Р.(соз д/^^-ф)""' • (115,5)

Уравнение же характеристик напишется в виде

0 = *tg(<p.-q>) + F(<p). (115,6)

Произвольная функция ^(ф) определится по заданной форме

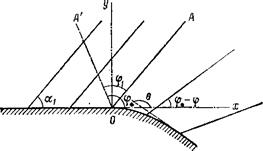
Рис. 115

профиля следующим образом. Пусть форма профиля задана урав­нением У=У(Х), где X и У— координаты его точек. На самой поверхности скорость газа направлена по касательной к ней, т. е.

tge=||. (115,7)

Уравнение прямой, проходящей через точку X, У и наклоненной под углом ф* — ф к оси х, есть

y-Y^(x-X) tg(«p.-q>).

Это уравнение совпадает с (115,6), если в последнем положить
Fto) = Y-Xtg(<p,-<p). (115,8)

Исходя из заданного уравнения Y=Y(X) и уравнения (115,7), представляем форму профиля в виде параметрических уравне­ний X = X(Q), У=У(6), где параметром является угол 9 на­клона касательной к профилю. Подставляя сюда 0, выраженное через tp согласно (115,4), получаем X и У в виде функций от ф} наконец, подставляя их в (115,8), получим искомую функцию F(cp).

При обтекании выпуклой поверхности угол 8 наклона вектора скорости к оси х уменьшается вниз по течению (рис. 115). Вместе с ним монотонно убывает также и угол ср» — ср наклона характеристик (речь идет везде о характеристиках, исходящих от тела) Благодаря этому характеристики нигде (в области те­чения) не пересекаются друг с другом. Таким образом, в области вниз по течению от характеристи­ки О А, которая будет представ­лять собой слабый разрыв, мы будем иметь непрерывный (без ударных волн) монотонно разре­жающийся поток.

Иначе обстоит дело при обте-
кании вогнутого профиля. Здесь___________________________

наклон 0 касательной к профилю, ⁱ'"?////u/sh//t'f////rf-
а с ним и наклон характеристик
возрастают в направлении тече- Рис. 116

ния. В результате характеристики

пересекаются друг с другом (в области течения). Но на различных не параллельных друг другу характеристиках все величины (скорость, давление и т. п.) имеют различные значе­ния. Поэтому в точках пересечения характеристик все эти функ­ции оказываются многозначными, что физически нелепо. Ана­логичное явление мы имели уже в нестационарной одномерной простой волне сжатия (§ 101). Как и там, оно означает здесь, что в действительности возникает ударная волна. Положение этого разрыва не может быть определено полностью из рас­сматриваемого решения, выведенного в предположении его от­сутствия. Единственное, что может быть определено, — это место начала ударной волны (точка О на рис. 116; ударная волна изображена сплошной линией ОВ). Она определяется как точка пересечения характеристик, лежащая на наиболее близкой к по­верхности тела линии тока. На линиях тока, проходящих под точкой О (ближе к телу), решение везде однозначно; в точке же О начинается его многозначность. Уравнения, определяющие координаты хо, Уо этой точки, могут быть получены аналогично тому, как были найдены соответствующие уравнения для опре­деления момента и места образования разрыва в одномерной не­стационарной простой волне. Если рассматривать угол наклона характеристик как функцию координат х и у точек, через кото­рые они проходят, то при значениях хну, превышающих не­которые определенные х₀, уо, эта функция делается многознач­ной. В § 101 мы имели аналогичное положение для функции v(x,t); поэтому, не повторяя заново всех рассуждений, напишем сразу уравнения

(*).-«■

определяющие здесь место начала ударкой волны. В математи­ческом отношении это — угловая точка огибающей семейства прямолинейных характеристик (ср. § 103).

Что касается области существования простой волны при об­текании вогнутого профиля, то вдоль линий тока, проходящих над точкой О, оно применимо вплоть до места пересечения этих линий с ударной волной. Линии же тока, проходящие под точ­кой О, с ударной волной вообще не пересекаются. Однако от­сюда нельзя сделать заключение о том, что вдоль них рассмат­риваемое решение применимо везде. Дело в том, что возникаю­щая ударная волна оказывает возмущающее влияние и на газ, текущий вдоль этих линий тока, и таким образом нарушает движение, которое должно было бы иметь место в ее отсутствии. В силу свойства сверхзвукового потока эти возмущения будут, однако, проникать лишь в область газа, находящуюся вниз по течению от характеристики ОА, исходящей из точки начала ударной волны (одна из характеристик второго семейства). Та­ким образом, рассматриваемое здесь решение будет применимым во всей области слева от линии АОВ. Что касается самой линии ОА, то она будет представлять собой слабый разрыв. Мы видим, что непрерывная (без ударных волн) во всей области простая волна сжатия вдоль вогнутой поверхности, аналогичная про­стой волне разрежения вдоль выпуклой поверхности, невоз­можна.

В ударной волне, возникающей при обтекании вогнутого про­филя, мы имеем пример волны, «начинающейся» от некоторой точки, расположенной в самом потоке вдали от твердых стенок. Такая точка «начала» ударной волны обладает некоторыми об­щими свойствами, которые мы здесь отметим. В самой точке на­чала интенсивность ударной волны обращается в нуль, а вблизи нее мала. Но в ударной волне слабой интенсивности скачок энтропии и ротора скорости — величины третьего порядка ма­лости, и потому изменение течения при прохождении через вол­ну отличается от непрерывного потенциального изэнтропического изменения лишь в величинах третьего порядка. Отсюда следует, что в отходящих от точки начала ударной волны слабых раз­рывах должны испытывать скачок лишь производные третьего порядка от различных величин. Таких разрывов будет, вообще говоря, два: слабый разрыв, совпадающий с характеристикой, и тангенциальный слабый разрыв, совпадающий с линией тока (см. конец § 96).

§ 116)

уравнение чаплыгина

§ 116. Уравнение Чаплыгина (общая задача

о двухмерном стационарном движении сжимаемого газа)

Рассмотрев стационарные простые волны, перейдем теперь к общей задаче о произвольном стационарном плоском потен­циальном движении. Говоря о потенциальном течении, мы под­разумеваем, что движение изэнтропично и что в нем отсутствуют ударные волны.

Оказывается возможным свести поставленную задачу к ре­шению всего одного линейного уравнения в частных производ­ных (С. А. Чаплыгин, 1902). Это осуществляется путем пре­образования к новым независимым переменным — компонентам скорости v_x, v_y (это преобразование часто называют преобразо­ванием годографа; плоскость переменных v_x, v_y называют при этом плоскостью годографа, а плоскость х, у — физической пло­скостью).

Для потенциального движения вместо уравнений Эйлера можно написать сразу их первый интеграл, т. е. уравнение Бер­нулли:

w+~^w₀. (116,1)

Уравнение непрерывности гласит:

4₇(pv_x) + -^-(pv_y) = 0. (116,2)

Для дифференциала потенциала ср скорости имеем:

dcp = v_x dx + Vy dy.

Произведем преобразование от независимых переменных х, у к независимым переменным v_x, v_y путем преобразования Ле-жандра. Для этого пишем:

dq> = d(xv_x) — xdv_x + d(yv_v) — ydv_y. Вводя функцию

Ф = — <f + xvx + yv„ (116,3)

получаем:

йФ = х dv_x + у dv_y,

где Ф рассматривается как функция от v_x и v_y. Отсюда имеем:

дФ дФ.„

* ⁼ 1£Г' ^{у =} -ЪЧу- ^(И6'⁴⁾

Удобнее, однако, пользоваться не декартовыми компонентами скорости, а ее абсолютной величиной v и углом 0, образуемым ею с осью х:

14 = о cos 9, v_y = vsinQ. (116.5)

Произведя соответствующее преобразование производных, легко получаем вместо (116,4) следующие соотношения:

_г — _гп, а ^{дФ sin 6 дФ} ___________ • о <5Ф, cosQ^ дФ,_llfiW

^X-^C0S(3^------------------- y-^sine^T + —— 1Г' ^(116,6)

Связь между потенциалом ф и функцией Ф дается при этом простой формулой

Ф = -Ф +»-^-. (116,7)

Наконец, для того чтобы получить уравнение, определяющее функцию Ф(у, G), надо преобразовать к новым переменным уравнение непрерывности (116,2). Написав производные в виде якобианов:

^d(f>^Vx> У)^д (Р^ру. X)

д (х, у) д (х, у) ~ ^U>

умножив на д(х, y)/d(v, 6) и подставив (116,5), имеем:

б (ррcos 0, у) _ д(pvsin 0, jc) _п

5 (w, G). д (у, 6) ~~^и*

При раскрытии этих якобианов надо подставить для х и у выра­жения (116,6). Кроме того, поскольку энтропия s является за­данной постоянной величиной, то, выразив плотность в виде функции от s и w и подставив для w выражение w = wo — v²/2, мы найдем, что плотность может быть написана в виде функции только от скорости: p = p(i;). Имея всё это в виду, получим после простых преобразований следующее уравнение:

d(pv) (дФ. 1 д²Ф\. дЩ __п dv {dv "¹" v дВ² P^v dv² ~ ^Jl

Согласно (83,5) имеем:

^-»0-£)

и в результате получим окончательно для функции Ф(у, 6) сле­дующее уравнение Чаплыгина:

<Э²Ф. у² д²Ф. дФ „ /11со\

¹ е²

Здесь скорость звука является заданной функцией скорости, c = c(v), определяемой уравнением состояния газа и уравне­нием Бернулли.

Уравнение (116,8) вместе с соотношениями (116,6) заменяет собой уравнения движения. Таким образом, задача о решении нелинейных уравнений движения сводится к решению линейного уравнения для функции Ф(и, 6). Правда, нелинейными оказы­ваются зато граничные условия для этого уравнения. Эти усло­вия заключаются в следующем. На поверхности обтекаемого тела скорость газа направлена по касательной к ней. Выразив координаты уравнения поверхности в виде параметрических уравнений X — X(Q), У = У (6) (как это было объяснено в пре­дыдущем параграфе) и подставив X и У в (116,6) вместо х и у, мы получим два уравнения, которые должны удовлетворяться при всех значениях 0, что возможно отнюдь не при всякой функ­ции Ф(и, 0). Граничное условие как раз и будет заключаться в требовании, чтобы оба эти уравнения были совместными при всех 0, т. е. одно из них должно быть автоматическим след­ствием другого.

Удовлетворения граничных условий, однако, еще не доста­точно для того, чтобы гарантировать пригодность полученного решения уравнения Чаплыгина для определения реального тече­ния во всей области движения в физической плоскости. Необ­ходимо еще выполнение следующего требования: якобиан

_д д (х, у)

д (8, v)

нигде не должен менять знак, проходя через нуль (за исклю­чением лишь тривиального случая, когда обращаются в нуль все четыре составляющие его производные). Легко видеть, что если это условие нарушается, то при прохождении через опре­деленную равенством Д = 0 (так называемую предельную) ли­нию в плоскости х, у решение, вообще говоря, становится комп­лексным¹). Действительно, пусть на линии v = Vo{Q) имеем А = 0 и пусть при этом (ду/дв)„ф0. Тогда имеем:

— д (А®_\ _ д (х, у) д (о, 6) _ д (х, у) _ (дх \ __п ^а \ду)_v д (v, 6) д (о, у) д (V, у) \ dv)_у ~~ ^и'

Отсюда видно, что вблизи предельной линии v как функция от х (при заданном у) определяется уравнением вида

*-*°⁼т(-ё-Х^(о-°^о)8'

*) Прохождение же через нуль путем обращения А в бесконечность не запрещается. Если на некоторой линии 1/Д = 0, то это приводит лишь к тому, что соответствие между плоскостями х, у и v, 0 становится не взаимно однозначным в том смысле, что при обходе плоскости х, у некоторая часть плоскости v, 9 проходится дважды или трижды. ²) Это утверждение остается, очевидно, справедливым и в тех случаях, когда одновременно с А обращается в нуль и (d²x/dv²)_y, но производная (dxldv)y по-прежнему меняет знак при v = о₀, т.е. разность х — Xq пропор­циональна более высокой четной степени v — v₀.

и по одну из сторон от предельной линии v становится комп­лексной ²).

Легко видеть, что предельная линия может появиться лишь в областях сверхзвукового движения. Непосредственное вычисле­ние с использованием соотношений (116,6) и уравнения (116,8) дает

ь=±[{-£к-Ш+^{Щ- сад

Цщо, что при v ^ с всегда А > 0, и лишь при v > с А может изменить знак, пройдя через нуль.

Появление в решении уравнения Чаплыгина предельных ли­ний свидетельствует о том, что в данных конкретных условиях невозможен непрерывный во всей области движения режим об­текания, и в потоке должны возникать ударные волны. Следует, однако, подчеркнуть, что положение этих волн отнюдь не совпа­дает с предельными линиями.

Дата добавления: 2014-11-07