Должно быть 4 страница

#±.£₊„„_о.

Кроме того, в простой волне (и на граничной характеристике) имеем:

,, dp. dw или ±с — dw/dv. Подставив это в написанное условие, получим:

dv ⁺ dw dv dv ^v'

откуда окончательно

% = -\f(v)dv, (105,11)

чем и определяется искомое граничное значение %. В частности, если простая волна центрирована в начале координат, т. е. / (у) = 0, то х = const; поскольку функция х вообще определена лишь с точностью до аддитивной постоянной, то в этом случае можно, не уменьшая общности, положить на граничной харак­теристике х = 0.

Задачи

1. Определить движение, возникающее при отражении центрированной волны разрежения от твердой стенки.

Решение. Пусть волна разрежения возникает в момент / = 0 в точке t = 0 1 распространяется в положительном направлении оси х; она дойдет

при

до стенки через промежуток времени t = l/со, где I — расстояние до стенки. На рис. 91 изображена диаграмма характеристик для процесса отражения волны В областях 1 я 1' газ неподвижен, в области 3 движется с постоян­ной скоростью v =*—U¹). Область 2 есть падающая волна разрежения (в прямолинейными характеристиками С+), а 5 — отраженная волна (с пря­молинейными характеристиками С_). Область 4 есть «область взаимодей­ствия», в которой должно быть най­дено решение; попадая в эту область, прямолинейные характеристики иск­ривляются. Это решение вполне оп­ределяется граничными условиями на отрезках аЬ и ас. На ab (т. е. на стенке) должно быть v — О при х = I; ввиду (105,1) имеем отсюда условие

в = 0.

Граница же ас с волной разрежения есть отрезок характеристики С_; по­этому на нем у — 1 v

2п+ 1

dv

■ const,

а поскольку в точке а имеем v ««= 0, с — со, то const = со. На этой границе должно быть х = 0, так что имеем условие

*~° ^при 5ГТТ*^Св-

Легко убедиться в том, что функция вида (105,9), удовлетворяющая этим условиям, есть

/(2л+1) / д \»^-1PlY о V 2l"\

чем и определяется искомое решение.

Уравнение характеристики ас есть (см. задачу § 103)

2п+1

■ (2я + 1) <у + 2 (я + 1) /(JSa.)⁵*"⁷

Ее пересечение с характеристикой Ос

2(я+1) ~^С°~ 2я+1

U

to

определяет момент исчезновения падающей волны:

п + \

Д2п+1)^я+Ч

[(2п + I) с₀ ~ U]

На рис. 91 предполагается, что U < 2с₀/(у+ 1); в противном случае ха­рактеристика Ос направлена в сторону отрицательных х (рис. 92). Процесс

') Если волна разрежения возникает от поршня, который начинает вы­двигаться из трубы с постоянной скоростью, то U есть скорость поршня.

взаимодействия падающей и отраженной волн длится при этом бесконечное (а не конечное, как на рис. 91) время.

Функция (I) описывает также и взаимодействие двух одинаковых цен­трированных волн разрежения, вышедших в момент времени t = 0 из точек к <== 0 и х = 21 и распространяющихся навстречу друг другу, как это оче­видно из соображений симметрии (рис. 93) ').

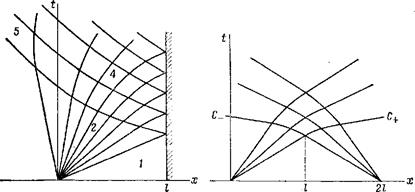
Рис. 92 Рис. 93

2. Вывести уравнение, аналогичное уравнению (105,3), для одномерного изотермического движения идеального газа.

Решение. Для изотермического движения в уравнении Бернулли вме­сто тепловой функции w стоит величина

S

dp 2С ^rfP 2, „

где с\ = (др/др)_т — квадрат изотермической скорости звука; у идеального газа в изотермическом случае с_т — const. Выбрав эту величину (вместо ш) в качестве независимой переменной, получим тем же способом, что и в тексте, для функции х следующее линейное уравнение с постоянными коэффициен­тами:

2 д²Х, дХ_ _ д²% _ _п ^Ст др.^{2 +} d|i dv²

§ 106. Задача о сильном взрыве

Рассмотрим распространение сферической ударной волны большой мощности, возникшей в результате сильного взрыва, т. е. мгновенного выделения в некотором небольшом объеме большого количества энергии (которую обозначим посредством Е); газ, в котором волна распространяется, будем считать по­литропный ').

') Излагаемое ниже решение этой задачи получено независимо Л. И. Сво­довым (1946) и Нейманом (/. von Neumann, 1947). С меньшей полнотой (без построения аналитического решения уравнений) задача была рассмотрена Тэйлором (G. I. Taylor, 1941, опубликовано в 1950).

Мы будем рассматривать волну на расстояниях, не слишком далёких от источника, в той области, где волна обладает еще большой интенсивностью. В то же время эти расстояния пред­полагаются большими по сравнению с размерами источника: это дает возможность считать, что выделение энергии Е прои­зошло в одной точке (в начале координат).

Большая интенсивность ударной волны означает, что скачок давления в ней очень велик. Мы будем считать, что давление р₂ позади разрыва настолько велико по сравнению с давлением Р\ невозмущенного газа впереди него, что

Это дает возможность везде пренебрегать pi по сравнению с р₂, причем отношение плотностей рг/pi будет равно своему предель­ному значению (у -f- 1) / (у —1) (см. § 89).

Таким образом, вся картина движения газа будет опреде­ляться всего двумя параметрами: начальной плотностью газа pi и выделяющейся при взрыве энергией Е. Из этих параметров и двух независимых неременных — времени t и координаты (рас­стояния от центра) г—можно составить всего одну независимую безразмерную комбинацию, которую мы напишем в виде

г(р1/£г²)'/⁶.

В результате все движение будет обладать определенной авто-модельностью.

Прежде всего можно утверждать, что положение самой удар^ ной волны в каждый момент времени должно соответствовать определенному постоянному значению указанной безразмерной комбинации. Тем самым сразу определяется закон перемещения ударной волны со временем; обозначив расстояние волны от центра посредством R, имеем

(106,1)

где В — числовая постоянная (зависящая от у), которая сама определится в результате решения уравнений движения. Ско» рость распространения ударной волны (скорость относительно невозмущенного газа, т. е. относительно неподвижной системы координат):

(106,2)

Таким образом, в рассматриваемой задаче закон движения удар­ной волны определяется (с точностью до постоянного множи­теля) уже из простых соображений размерности.

Давление ри плотность pi и скорость v₂ = и₂ — "i газа (отно­сительно неподвижной системы координат) на «задней» стороне разрыва могут быть выражены через и\ по полученным в § 89 формулам. Согласно (89,10—11) имеем¹):

"2 = 7^7"!. P₂ = Pi^f- P2=7^TPi",- (106,3)

Плотность остается постоянной во времени, a v₂ и р₂ убывают соответственно как t~^zlb и г-^6/5. Отметим также, что создаваемое ударной волной давление р₂ растет с увеличением полной энер­гии взрыва как Е²'^ъ.

Перейдем, далее, к определению движения газа во всей об­ласти за ударной волной. Введем вместо скорости v, плотности р газа и квадрата с² = ур/р скорости звука в нем (который за­менит собой переменную р — давление) безразмерные перемен­ные V, G, Z, определив их посредством ²)

o=-gf-K. p = p,G, c² = -^-Z. (106,4)

Величины V, G, Z могут быть функциями только одной безраз­мерной независимой «автомодельной» переменной, которую опре­делим как

*=w=i(iM^,/5- ⁽¹⁰⁶'⁵⁾

В соответствии с (106,3), на поверхности разрыва (т. е. при § = 1) они должны принимать значения

V(»=4TT- G(l) = Jf±f. Z(l) = ^^i. (106,6)

Уравнения центрально-симметричного адиабатического дви­жения газа гласят:

dv, dv ____ 1 dp ^дР I d(pv). 2po ___________ „

Z >\ * <««»>

O+'i)"¹*-⁰-

') Определяемые формулами (89,11) скорости ударной волны относитель­но газа мы обозначаем здесь как Ui и «2. ²) Не смешивать обозначение V в этом и следующем параграфах с обо-аначением удельного объема в других местах!

Последнее уравнение есть уравнение сохранения энтропии, в ко­торое подставлено выражение (83,12) для энтропии политроп­ного газа. После подстановки выражений (106,4) получается си­стема уравнений в полных производных для функций V, G, Z. Интегрирование этой системы облегчается тем, что один из ее

интегралов может быть написан непосредственно из следующих соображений.

Тот факт, что мы пренебрегаем давлением р_х невозмущенного газа, означает, другими словами, что мы пренебрегаем первона­чальной энергией газа по сравнению с энергией Е, приобретае­мой им в результате взрыва. Поэтому ясно, что полная энергия газа внутри ограниченной ударной волной сферы постоянна (и равна Е). Более того, ввиду автомодельности движения оче­видно, что должна оставаться неизменной энергия газа и внутри любой сферы меньшего радиуса, расширяющейся со временем по закону g = const с любым (а не только равным |₀) значе­нием const; радиальная скорость перемещения точек этой сферы равна v_n = 2r/5t (ср. (106,2)).

Легко написать уравнение, выражающее это постоянство энергии. С одной стороны, в течение времени dt через поверх­ность сферы (площади 4яг²) уходит энергия

dMnr²pu (до -f ~y) •

С другой стороны, за это же время объем сферы увеличивается на элемент dtv_n4nr², внутри которого заключен газ с энергией

dt4nr²o_np (е + -j-).

Приравняв эти два выражения друг другу, подставив е и до из (83, 10—11) и введя безразмерные функции согласно (106,4), получим соотношение

^Z 2(yV-1) ¹ (106,8)

которое и является искомым интегралом системы уравнений. Он автоматически удовлетворяет граничным условиям (106,6).

После установления интеграла (106,8) интегрирование си­стемы уравнений элементарно, хотя и громоздко. Второе и третье из уравнений (106,7) дают

^dV ~(1-Ю-таг--зу.

ding ^{v ;} ding

din Z. dlnG _ 5-2V (106,9)

ding W ^l) din I ~"~ 1-V ^-

Из этих двух уравнений о помощью соотношения (106,8) выра­жаем производные dV/dln| и d In G/dV в виде функций толь­ко от V, после чего интегрирование с учетом граничных условий

(106,6) приводит к следующим результатам:

И^Г^!{^1⁵-^-1><[^-.)]''.

v (Ю6,10)

13у²-7у+12 _ Б(у-1) _ 3

^Vl— (Зу- 1)(2у+ О ' ² -2Y+1 ' ³ 2у+1*
v, 2

Формулы (106,8), (106,10) дают полное решение поставлен­ной задачи. Постоянная 8, входящая в определение независимой переменной |, определяется условием

£=^р(^ + ₇т^г_ТГ)4лг²йг,

выражающим равенство полной энергии газа энергии взрыва £. После введения безразмерных величин это условие принимает вид

е⁵тИ^ + -у1^=Т)]^=^{К (106}>^П)

о

Так, для воздуха (у = 7/5) оказывается 6 = 1,033.

Из формул (106,10) легко видеть, что при £->0 функция V стремится к постоянному пределу, а функция G — к нулю по законам

V — -у со |⁵/^vs G со gw*.

Отсюда следует, что отношения и/у₂ и р/р₂ как функции отно­шения r/R = I стремятся при |->0 к нулю по законам

v/v₂ ос r/R, р/р₂ оо (r//?)^3/(v-¹⁾; (106,12)

*) Эти утверждения относятся к значениям у •< 7 (при этом функция V(%) меняется от значения V(l) == 2/(у+ 1) до V'(0) = 1/у). Для реальных газов, термодинамические функции которых мсжно было бы аппроксимиро­вать формулами для. политропного газа, это неравенство заведомо выполня­ется (фактически верхним пределом y является в этом смысле значение 5/3, отвечающее одноатомному газу). Укажем, однако, для формальной полноты, что при у > 7 функция V(5) меняется от значения 2/(y+ 1) при | «=» 1 до предельного значения 1, достигаемого при определенном (зависящем от у) значении I = &)•< 1"» в этой точке функция G обращается в нуль, т. е. возни­кает расширяющаяся сферическая область пустоты.

отношение же давлений р/р₂ стремится к постоянному пределу, а отношение температур — соответственно к бесконечности¹).

1,0

0,5

На рис. 94 изображены графически величины и/и₂, р/р₂ и р/р₂ как функции r/R для воздуха {у = 1,4). Обращает на себя внимание очень быстрое убывание плотности по направлению внутрь сферы: почти все вещество сконцентрировано в сравни­тельно узком слое позади фрон­та ударной волны. Это обстоя­тельство является естествен­ным следствием того, что по поверхности наибольшего, рав­ного R, радиуса должно быть распределено вещество с ше­стикратной по сравнению с нор­мальной плотностью¹).

§ 107. Сходящаяся сферическая ударная волна

Рядом поучительных осо­бенностей обладает задача о сходящейся к центру ударной волне большой интенсивно­сти ²). Вопрос о конкретном ме­ханизме возникновения такой волны нас не будет интересовать; достаточно представлять себе, что волна создана каким-то «сферическим поршнем», сообщаю­щим газу начальный толчок; по мере схождения к центру волна усиливается.

Мы будем рассматривать движение газа на той стадии про­цесса, когда радиус R сферической поверхности разрыва уже мал по сравнению с ее начальным радиусом — радиусом «поршня» R₀. На этой стадии характер движения в значитель­ной степени (ниже будет видно — какой) не зависит от конкрет­ных начальных условий. Ударную волну будем считать уже на­столько сильной, что давлением р\ газа перед ней можно (как и в предыдущем параграфе) пренебречь по сравнению с давле­нием р2 позади нее. Что касается полной энергии газа, заклю­ченной в рассматриваемой (переменной!) области г ~ R <С Ro, то она отнюдь не постоянна (как будет видно ниже —убывает со временем).

') Результаты вычислений для других значений у, а также аналогичное решение задачи о сильном взрыве в случае цилиндрической симметрии при­ведены Л. И. Седовым в книге «Методы подобия и размерности в механике», изд. 9 —М.: Наука, 1981, гл. IV, § 11. ²) Эта задача была рассмотрена независимо Гудерлеем (О. Guderleu, 1942) и Л. Д. Ландау и К. П. Станюковичем (1944, опубликовано в 1955).

Пространственный масштаб рассматриваемого движения мо­жет определяться лишь самим, меняющимся со временем, ра­диусом ударной волны R(t), а масштаб скорости — производной dR/dt. В этих условиях естественно предположить, что движе­ние будет автомодельным, с независимой «автомодельной пере­менной» | = r/R(t). Однако зависимость R(t) нельзя определить из одних только соображений размерности.

Примем момент фокусировки ударной волны (т. е. момент, когда R обращается в нуль) в качестве t — 0. Тогда времени до фокусировки отвечают значения / < 0. Будем искать функцию R(t) в виде

#(/) = A (-tf (107,1)

с неизвестным заранее показателем автомодельности а. Ока­зывается, что этот показатель определяется условием существо­вания самого решения уравнений движения (в области г <С Ro) с надлежащими граничными условиями. Тем самым определяется и размерность постоянного параметра А. Величина же этого па­раметра остается неопределенной и может быть, в принципе, найдена лишь путем решения задачи о движении газа в целом, т. е. путем сшивки автомодельного решения с решением на рас­стояниях г ~ Ro, зависящим от конкретных начальных условий. Именно через этот параметр, и только через него, зависит дви­жение при R «С Ro от способа начального создания ударной волны.

Покажем, как осуществляется решение поставленной таким образом задачи.

Подобно тому, как это было сделано в § 106, введем безраз­мерные неизвестные функции согласно определениям

*⁼Ж ⁼ 7(^ ^(107>3)

(при а = 2/5 определения (107,2) совпадают с (106,4)). Напом­ним, что v — радиальная скорость газа относительно неподвиж­ной системы координат, связанной с неподвижным газом внутри сферы г = Ro, газ движется вместе с ударной волной по направ­лению к центру, чему отвечает v < 0 (так что V'(|)> 0).

Фактически искомое решение уравнений движения относится лишь к области г ~ R позади ударной волны, и к достаточно малым временам t (при которых R -С Ro). Но формально полу­чаемое решение охватывает все пространство г ^ R—-от по­верхности разрыва до бесконечности, и все времена t ^ 0; при этом переменная £ пробегает все значения от 1 до оо. Соответ­ственно, граничные условия для функций G, V, Z должны быть поставлены при I — 1 и g = оо,

Значение | = 1 отвечает поверхности ударной волны; гранич­ные условия на ней совпадают с (106,6).

Для установления условий на бесконечности (по £) заме­чаем, что при t = 0 (в момент фокусировки волны) все вели­чины v, р, с² на всех конечных расстояниях от центра должны оставаться конечными. Но при t = 0, г ф 0 переменная \ = со. Для того чтобы функции v (r,t) и c²(r,t) при этом оставались конечными, функции V(£) и Z(g) должны обращаться в ноль,

у (00) = 0, Z(oo) = 0. (Ю7,4>

После подстановки (107,2—3), система уравнений (106,7) принимает вид

Л _ i/\ dV _ Z dlnG ____________ 1 dZ __ 2 у _ _у (\___________.,\

* 'ding Yd ln| Yd In I Y U / '

^dV ■0-V)4S?—ЗУ. (107.6)

dIn § ^v* ⁷ dIn I, _n7 dlnG dZ _ 2Z(\/a—V) W ^1,Z ding ding ~ \-V

(последние два уравнения — ср. с (106,9)). Отметим, что незави­симая переменная g входит в эти уравнения только в виде диф­ференциала ding; постоянная In Л при этом выпадает из урав­нений вовсе и, следовательно, остается неопределенной — в соот­ветствии со сказанным выше.

Коэффициенты при производных в уравнениях (107,5) и-их правые части содержат только V и Z (но не G)¹). Решив эти уравнения относительно производных, мы выразим последние через эти две функции. Таким образом, получим уравнения

_d]nj__ Z-(\ - V)² nnrfiV

dV ~ (ЗУ — x)Z—V(\ — V) (1/ct — V) ' UO/,o;

₍₁ - V) -gJLg- = 3V - «^V -»> ^Z_Z-_^V_{?S$ ^(m ~ ^V) (Ю7.7)

(где v. ==2(1 — а)/ау). В качестве же третьего напишем уравне­ние, получающееся делением производной dZ/d In g на dV/d\r\\\ оно гласит:

dZ _ Z ([Z-(l-V)²][2/a-(3y-l)V]. Л,

dV ~ 1-У I (3V-x)Z-V(\-V)(\/a-V) "^t"^Y J' ^^lu''°'

Если найдено нужное решение уравнения (107,8), т. е. функцио­нальная зависимость Z(V),to после этого решение уравнений (107,6—7) (нахождение зависимости l(V) и затем G(Q) сво­дится к квадратурам.

') Именно в этом состоит преимущество введения в качестве основных переменных и, р, с² вместо v, р, р.

Таким образом, вся задача сводится прежде всего к решению уравнения (107,8). Интегральная кривая на плоскости V, Z должна выходить из точки (назовем ее точкой У) с координа­тами У(1), 2(1) — «образа» ударной волны на плоскости V, Z. Указанием этой точки уже определяется решение уравнения (107,8) (при заданном а): интегральная кривая уравнения пер­вого порядка однозначно определяется заданием одной (не осо­бой) ее точки. Выясним условие, позво­ляющее установить значение а, приводя­щее к «правильной» интегральной кри­вой.

Это условие возникает из очевидного физического требования: зависимости всех величин от | должны быть однозначны­ми — каждому значению | должны отве­чать единственные значения V, G, Z. Это значит, что во всей области изменения пе­ременной | (1 ^ с оо, т. е. 0 ^ In | ^ <со) функции |(V), |(G), |(Z) не должны иметь экстремумов. Другими сло­вами, производные d In \/dV,... должны нигде не обращаться в нуль. На рис. 95 Y_ кривая/ — парабола

Z = (l — V)². (107,9)

Легко видеть, что точка У лежит над ней¹). Между тем, ин­тегральная кривая, отвечающая решению поставленной задачи, должна прийти в начало координат — в соответствии с предель­ным условием (107,4); поэтому она непременно пересекает па­раболу (107,9). Но все указанные производные выражаются, согласно (107,6—8), дробными выражениями, в числителе кото­рых стоит разность Z —(1 — V)². Для того чтобы эти выраже­ния не обращались в нуль в точке пересечения интегральной кривой с параболой (107,9), должно одновременно быть

(3V — x)Z=V(l — V)(\/a—V). (107,10)

Другими словами, интегральная кривая должна проходить че­рез точку пересечения параболы (107,9) с кривой (107,10) (кри­вая 2 на рис. 95); эта точка —особая точка уравнения (107,8) (производная dZ/dV = 0/0). Этим условием и определяется зна­чение показателя автомодельности а; приведем два значения, получающиеся в результате численных расчетов:

а = 0,6884 при у = 5/3; а = 0,7172 при у = 7/5. (107,11)

') Это обстоятельство выражает собой просто тот факт, что скорость таза на задней стороне поверхности разрыва меньше скорости звука в нем.

Пройдя через особую точку, интегральная кривая устрем­ляется в начало координат (точка О), отвечающее предельным значениям (107,4). Для уяснения математической ситуации, опи­шем кратко картину распределения интегральных кривых урав­нения (107,8) на плоскости V, Z (при «правильном» значе­нии а), не проводя соответствующих вычислений ').

Кривые (107,9) и (107,10) пресекаются, вообще говоря, в двух точках — кружки на рис. 95 (помимо несущественной точки

V = 1, Z = 0 на оси абсцисс). Кроме того, уравнение имеет осо­бую точку с в пересечении кривой (107,10) с прямой (Зу— 1) V= = 2/а (обращение в нуль второго множителя в числителе в (107,8)). Точка а, через которую проходит «правильная» инте­гральная кривая — точка типа седла; точки Ъ и с — узлы. Узло­вой особой точкой является также и начало координат 0. Вблизи последнего уравнение (107.8) принимает вид

dz ^ 22 dV V + xZ '

Элементарное интегрирование этого однородного уравнения по­казывает, что при V-*-0 функция Z(V) стремится к нулю бы­стрее, чем V, а именно

Z~ const -V². (107,13)

Таким образом, из начала координат выходит бесконечное мно­жество интегральных кривых (отличающихся значением const в (107,12)). Все эти кривые входят затем в узел Ъ или узел с — за исключением лишь одной, входящей в седловую точку а (одна из двух сепаратрис — единственных интегральных кри­вых,, проходящих через седло)²).

Началу координат отвечает | = оо, т. е. момент фокусировки ударной волны в центре. Определим предельные распределения всех величин по радиальным расстояниям в этот момент. С уче­том (107,12) из уравнений (107,6—7) найдем, что

V = const-r^1/0, Z = const • \~^2,а, G = const при £->оо (107,13)

²) Описанная картина, как оказывается, имеет место лишь при у < yi = ■=1,87... При у — Yi ^и «правильном» а точки а и Ь сливаются, а цри Y > Yt картина распределения интегральных кривых меняется и требуется более глубокое исследование. Напомним, однако, что в физически реальных случаях у ^ 5/3 (ср. примечание на стр. 562).

(значения постоянных коэффициентов могут быть найдены толь­ко путем фактического численного определения интегральной кривой на всем ее протяжении). Подставив эти выражения в оп­ределения (107,2), получим¹)

| о | оо с со _r-w«-D, p = const, р оо г-²"/«-'). (107,14)

Эти законы можно было бы найти и прямо из соображений раз­мерности (после того, как стала известной размерность А). В на­шем распоряжении имеется два параметра, pi и А, и одна пе­ременная г; из них можно составить всего одну комбинацию размерности скорости: A^llar^l-^l,a\ величиной же с размерностью плотности является лишь само рь

Найдем еще закон, по которому меняется со временем пол­ная энергия газа в области автомодельного движения. Размеры (по радиусу) этой области — порядка величины радиуса R ударной волны и уменьшаются вместе с ним. Примем условно за границу автомодельной области некоторое определенное зна­чение r/R = \i. Полная энергия газа в сферическом слое между радиусами R и l\R после введения безразмерных переменных выражается интегралом

(ср. (106,11)). Интеграл здесь — постоянное число²). Поэтому находим, что

£_а-т ~ #⁵~^2/" оо (- /)^5а-². (107,15)

Для всех реальных значений у, показатель степени здесь поло­жителен. Хотя интенсивность самой ударной волны растет по мере ее приближения к центру, но в то же время уменьшается объем области автомодельного движения и это приводит к уменьшению полной заключенной в ней энергии.

После фокусировки в центре возникает «отраженная» удар­ная волна, расширяющаяся (при t > 0) навстречу движущемуся к центру газу. Движение в этой стадии тоже автомодельно, с тем же показателем автомодельности а, так что закон расширения R оо t^a. Более подробным исследованием этого движения мы здесь заниматься не будем ³).

') Предельное значение отношения p/pj в момент фокусировки равно 20,1 для у = 7/5 и 9,55 для у = 5/3. ²) Интеграл расходится при gi -*■ оо. Это обстоятельство — следствие не- применимости автомодельного режима на расстояниях г;» R. ³) Укажем лишь, что отражение ударной волны сопровождается дальней- шим сжатием вещества, достигающим 145 для у = 7/5 и 32,7 для у = 5/3.

Таким образом, рассмотренная задача дает пример автомо­дельного движения, в котором, однако, показатель автомодель­ности (т. е. вид автомодельной переменной |) не может быть

определен из соображений размерности; он определяется лишь, в результате решения самих уравнений движения, с учетом усло­вий, диктуемых физической постановкой задачи. С математиче­ской точки зрения характерно, что эти условия формулируются как требование прохождения интегральной кривой дифференци­ального уравнения первого порядка через его особую точку. При этом показатель автомодельности оказывается, вообще говоря, иррациональным числом').

§ 108. Теория «мелкой воды»

Замечательную аналогию движению сжимаемого газа пред­ставляет движение в поле тяжести несжимаемой жидкости со свободной поверхностью, если глубина слоя жидкости достаточно мала (мала по сравнению с характеристическими размерами за­дачи, например, по сравнению с размерами неровностей дна во­доема). В этом случае поперечной компонентой скорости жид: кости можно пренебречь по сравнению с продольной (вдоль слоя) скоростью, а последнюю можно считать постоянной вдоль толщины слоя. В этом приближении (называемом гидравличе­ским) жидкость можно рассматривать как «двухмерную» среду, обладающую в каждой точке определенной скоростью v и, кроме того, характеризующуюся в каждой точке значением величины h — толщины слоя.

Соответствующие общие уравнения движения отличаются от уравнений, полученных в § 12, лишь тем, что изменения величин при движении не должны предполагаться малыми, как это де­лалось в § 12 при изучении длинных гравитационных волн малой амплитуды; в связи с этим в уравнении Эйлера должны быть со­хранены члены второго порядка по скорости. В частности, для одномерного движения жидкости в канале, зависящего только от одной координаты х (и времени), эти уравнения имеют вид

Дата добавления: 2014-11-07