Должно быть 1 страница

ДФ

Р2

Pi

= 1 +

Y(V+ \)U² 4_С?

+

yU_

(v+ \)²u²

16c²

Зная pi, можно вычислить согласно формулам (89,4) скорость ударной волны отнбсительно газов впереди и позади нее. Поскольку газ / покоится, то ско­рость волны относительно него есть скорость ее распространения по трубе. Если координата х вдоль длины трубы отсчитывается от начального места нахождения поршня (причем газ находится со стороны х > 0), то для поло­жения ударной волны в момент t получим:

+ О²

(положение же поршня есть х = Ut).

2. То же, если поршень выдвигается из трубы со скоростью U. Решение. К поршню примыкает область газа (/ на рис. 76,о), дви­жущегося в отрицательном направлении оси х с постоянной скоростью — U,

равной скорости поршня. Далее следует волна разрежения 2, в которой газ движется в отрица­тельном направлении оси л: со скоростью, меняю­щейся от значения —U до нуля по линейному закону (99,17). Давление же меняется по за­кону (99,16) от значения

2у

Y-1

Pi

(c-U)t

в газе / до Ро в неподвижном газе 3. Граница области 2 с областью /, определяется условием v = —U; согласно (99,17) получим:

Y + 1

х = (с₀

(с —скорость звука в газе /). На границе же с областью 3 v — 0, откуда х = Cot- Обе эти границы представляют собой слабые разрывы, из которых второй всегда распространяется вправо (т. е. в сторону от поршня); первый же (граница /—2) может распространяться как вправо (как это изображено на рис. 76,а), так и влево —если скорость поршня U > 2с₀/(у + 1).

Описанная картина может иметь место только при условии U<2col(y—1). Если же U>2c₀j(y—1), то перед поршнем образуется область вакуума (газ как бы не успевает двигаться за поршнем), прости­рающаяся от поршня до точки с координатой x=—2cot/(y—1) (1 на рис. 76,6). В этой точке v = — 2с₀/(у~-1); за ней следует область 2, в кото­рой скорость падает до нуля (в точке х = c₀t), а дальше область 3 непо­движного газа.

3. Газ находится в цилиндрической трубе, не ограниченной с одной сто­роны (х > 0) и закрытой заслонкой с другой (* = 0). В момент времени t = 0 заслонка открывается, и газ выпускается в наружную среду, давление р_е которой меньше первоначального давления _Ро в трубе. Определить возни­кающее движение газа.

Решение. Пусть —v_e есть скорость газа, соответствующая по формуле (99,16) внешнему давлению р„; при х = 0, г>0 должно быть v = — v_e. Если v_e < 2с₀/ (у + 1). ^т0 получается картина распределения скорости, изо­браженная на рис. 77,а. При v_e = 2с₀/(у + 1) (что соответствует скоростд вытекания, равной местной скорости звука на выходе трубы, — в этом легко убедиться, положив v — с в формуле (99,14)) область постоянной скорости

2Сп

исчезает и получается картина, изображенная на рис. 77, б. Величина —-j—j-

представляет собой наибольшую возможную скорость вытекания газа из тру­бы в рассматриваемых условиях. Если внешнее давление

Ре < Ро

(v+i)

Y-1

(О

то соответствующая ему скорость v_e сделалась бы больше, чем 2с₀/(у+1). В действительности при этом давление на выходе трубы будет продолжать оставаться равным предельному значению (1), а скорость вытекания — равной 2с₀/(у+1); остальное падение давления (до р_е) происхо­дит во внешней среде.

4. Бесконечная труба перегорожена порш­нем, по одну сторону от которого (х < 0) в начальный момент времени находится газ под давлением р₀, а по другую сторону (л; > 0) — вакуум. Определить движение поршня под влиянием расширяющегося газа.

л. Y-1

Решение. В газе возникает волна раз­режения, одна из границ которой перемеща­ется вместе с поршнем вправо, а другая — вле­во. Уравнение движения поршня

dU (. у-1 U \

(U—скорость поршня, т-Интегрируя, получим:

■ масса, приходящаяся на единицу его площади).

■ (V + 1) Ро Л

2тс₀ J

Y-1 Y+l

5. Определить движение в изотермической автомодельной волне разре­жения.

Решение. Изотермическая скорость звука

и при постоянной температуре с_Т = const = с_То- Согласно (99,5—6) находим поэтому:

. Р, Р *
v — c_T In -Z— = C_T In-*-— = — с_т.

Ро ^П Ро t ^Т°

6. С помощью уравнения Бюргерса (§ 93) определить связанную с дис­сипацией структуру слабого разрыва между волной разрежения и неподвиж­ным газом.

Решение. Пусть неподвижный газ находится слева, а волна разреже­ния — справа от слабого разрыва (тогда последний движется влево). Без учета диссипации, в первой из этих областей имеем v = 0, а во второй дви­жение описывается уравнениями (99,5—6) (с обратным знаком перед с), при­чем вблизи разрыва скорость v мала; с точностью до членов первого порядка по v имеем

f-'-«"-^co₊(l ₊ -g-|^) = -_C„ ₊ a„_0>

где а определено в (102,2), а индекс 0 указывает значения величин при v = 0 (ниже этот индекс опускаем).

С точностью до величин второго порядка малости скорость в волне, рас­пространяющейся влево, подчиняется полученному в задаче 1 § 93 уравне­нию (6), или уравнению Бюргерса

ди дид²и

~bT ^{+ u}~dT~^ll~dV'

где р. = ас³, а неизвестная и = av выражена в функции от / и £ = х -4- ct; переменная £ измеряет расстояние от слабого разрыва в каждый момент вре­мени г. Требуется найти непрерывное решение этого уравнения с граничными условиями

u=yt при £-^оо, и — 0 при £->-— оо,

отвечающими движению без учета диссипации. В соответствии с законом рас­ширения слабого разрыва (96,1), переменная t должна входить в решение в комбинации z — ll-\fT с переменной £. Такое решение может удовлетво­рять поставленным граничным условиям, если

Функция ф связана с введенной в задаче 2 § 93 функцией ср соотношением

-2р. 1п_Ф= ^ф(₂)-^- = $Ф0г)~, так что ф зависит только от г, причем

ф(г) = -2р.г-^-1п<р(г).

Уравнение (3) указанной задачи принимает вид 2рф" = —гф', откуда

ф(₂)= J _e~^z'^dz.

Решение, удовлетворяющее граничным условиям:

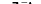или окончательно для скорости»(£, t):

^а L с/г VS*

чем и определяется структура слабого разрыва.

§ 100. Разрывы в начальных условиях

Одной из важнейших причин возникновения поверхностей разрыва в газе могут являться разрывы в начальных условиях движения. Начальные условия (т. е. начальные распределения скорости, давления и т. п.) могут быть заданы, вообще говоря, произвольным образом. В частности, эти начальные распределе­ния отнюдь не должны быть непременно везде непрерывными функциями и могут испытывать разрывы на некоторых поверх­ностях. Так, если в некоторый момент времени привести в со­прикосновение две массы газа, сжатые до различных давлений, то поверхность их соприкосновения будет поверхностью разрыва в начальном распределении давления.

Существенно, что скачки различных величин в разрывах на­чальных условий (или, как мы будем говорить, в начальных разрывах) могут быть совершенно произвольными; между ними не должно существовать никаких соотношений. Между тем, мы знаем, что на поверхности разрывов, которые могут существо­вать в газе в качестве устойчивых образований, должны соблю­даться определенные условия; так, скачки плотности и давления в ударной волне связаны друг с другом ударной адиабатой. По­этому ясно, что если в начальном разрыве эти необходимые ус­ловия не соблюдаются, то в дальнейшем он во всяком случае не сможет продолжать существовать как таковой. Вместо этого начальный разрыв, вообще говоря, распадается на несколько разрывов, каждый из которых является каким-нибудь из воз­можных типов разрывов (ударная волна, тангенциальный раз­рыв, слабый разрыв); с течением времени эти возникшие раз­рывы будут отходить друг от друга ').

В течение малого промежутка времени, начиная от началь­ного момента t = 0, разрывы, на которые распадается началь­ный разрыв, еще не успеют разойтись на большие расстояния друг от друга, и потому вся исследуемая картина движения бу­дет ограничена сравнительно узким объемом, прилегающим к поверхности начального разрыва. Как обычно, достаточно рас­сматривать в общем случае отдельные участки поверхности на­чального разрыва, каждый из которых можно считать плоским. Поэтому можно ограничиться рассмотрением плоской поверх­ности разрыва. Мы выберем эту плоскость в качестве плоскости у, г. Из соображений симметрии очевидно, что разрывы, на ко­торые распадется начальный разрыв при г>0, будут тоже пло­скими и перпендикулярными к оси х. Вся картина движения бу­дет зависеть только от одной координаты х (и времени), так что задача сводится к одномерной. Благодаря отсутствию каких бы то ни было характеристических параметров длины и вре-

') Общее исследование этого вопроса дано Н. Е. Кочиным (1926), мени, задача автомодельна, и мы можем воспользоваться полу­ченными в предыдущем параграфе результатами.

Разрывы, возникающие при распаде начального разрыва, должны, очевидно, двигаться от места их образования, т. е. от места нахождения начального разрыва. Легко видеть, что при этом в каждую из двух сторон (в положительном и отрицатель­ном направлениях оси х) может двигаться либо одна ударная волна, либо одна пара слабых разрывов, ограничивающих волну разрежения.- Действительно, если бы, скажем, в положительном направлении оси х распространялись две образовавшиеся в од­ном и том же месте в момент t — О ударные волны, то передняя из них должна была бы двигаться со скоростью большей, чем скорость задней волны. Между тем согласно общим свойствам ударных волн первая должна двигаться относительно остаю­щегося за ней газа со скоростью, меньшей скорости звука с в этом газе, а вторая должна двигаться относительно того же газа со скоростью, превышающей ту же величину с (в области между двумя ударными волнами с = const), т. е. должна догонять первую. По такой же причине не могут следовать друг за дру­гом в одну и ту же сторону ударная волна и волна разрежения (достаточно заметить, что слабые разрывы движутся относи­тельно газов впереди и позади них со звуковой скоростью). На­конец, две одновременно возникшие волны разрежения не могут разойтись, так как скорость заднего фронта первой равна ско­рости заднего фронта второй.

Наряду с ударными волнами и волнами разрежения при рас­паде начального разрыва должен, вообще говоря, возникнуть так же и тангенциальный разрыв. Такой разрыв во всяком слу­чае необходим, если в начальном разрыве испытывали скачок поперечные компоненты скорости v_y, v_z- Поскольку эти компо­ненты скорости не меняются ни в ударной волне, ни в волне разрежения, то их скачок будет всегда происходить на танген­циальном разрыве, остающемся на том же месте, где находился начальный разрыв; с каждой стороны от этого разрыва v_y, v_z будут оставаться постоянными (в действительности, конечно, благодаря неустойчивости тангенциального разрыва со скачком скорости он, как всегда, с течением времени размоется в турбу­лентную область).

Тангенциальный разрыв, однако, должен возникнуть даже и в том случае, когда v_y, v_z не имеют скачка в начальном раз­рыве (не ограничивая общности, можно считать в этом случае, что постоянные v_y и v_z равны нулю, что и будет подразумеваться ниже). Это показывают следующие соображения. Возникающие в результате распада разрывы должны дать возможность пе­рейти от заданного состояния 1 газа с одной стороны начального разрыва к заданному состоянию 2 с другой стороны. Состояние газа определяется тремя независимыми величинами, например,

з'

р, р н v_x = v. Поэтому необходимо иметь в распоряжении три произвольных параметра для того, чтобы посредством некото­рого набора разрывов перейти, скажем, от состояния / к про­извольно заданному состоянию 2. Но мы знаем, что ударная волна (перпендикулярная к направлению потока), распростра­няющаяся по газу, термодинамиче­ское состояние которого задано, пол­ностью определяется одним пара­метром (§ 85). То же самое относит­ся к волне разрежения (как видно из формул (99,14—16), при задан­ном состоянии входящего в волну Н^У^ТУ^. разрежения газа состояние выходя­щего газа полностью определится заданием одной из величин в нем). С другой стороны, мы видели, что в результате распада в каждую сто­рону может пойти не более одной волны — ударной или разрежения. Таким образом, мы будем иметь в нашем распоряжении всего два па­раметра, что недостаточно.

х

я— Р^ВР_

г)

- ударная волна - тангенц. разрыв - слабый разрыв Рис. 78

Возникающий на месте началь­ного разрыва тангенциальный раз­рыв как раз и представляет этот не­достающий третий параметр. На ""*^р-ТР_^ этом разрыве остается непрерывным давление; плотность же (а с ней и температура, энтропия) испытывает скачок. Тангенциальный разрыв не­подвижен относительного газа по обеим его сторонам, и потому к нему не относятся использованные выше соображения о взаимном обгоне двух распространяющихся в одном направлении волн.

Газы, находящиеся по обе сто­роны тангенциального разрыва, не

перемешиваются друг с другом, так как движения газа через тангенциальный разрыв нет; во всех перечисленных ниже ва­риантах эти газы могут быть даже газами различных веществ.

На рис. 78 схематически изображены все возможные типы распада начального разрыва. Сплошной линией изображен ход изменения давления вдоль оси х (изменение плотности изобра­зилось бы линией такого же характера, с той лишь разницей, что имелся бы скачок также и на тангенциальном разрыве). Вертикальные отрезки изображают образовавшиеся разрывы, а стрелками указаны направления их распространения и направ­ления движения газа. Система координат выбрана везде та, в которой тангенциальный разрыв покоится; вместе с ним покоит­ся также и газ в прилегающих к нему областях 3, 3'. Давления, плотности и скорости газов в крайних слева и справа областях 1 и 2 — это те значения соответствующих величин, которые они имеют в момент времени t — О на обеих сторонах начального разрыва.

В первом случае (который мы условно записываем в виде +, рис. 78, а) из начального разрыва Н возникают две ударные волны У, распространяющиеся в противоположные стороны, и расположенный между ними тангенциальный разрыв Т. Этот случай осуществляется при столкновении двух масс газа, движущихся с большой скоростью навстречу друг другу.

В случае Н У(рис. 78,6) по одну сторону от тан­генциального разрыва распространяется ударная волна, а по другую — волна разрежения Р. Этот случай осуществляется, на­пример, если в начальный момент времени приводятся в сопри­косновение две неподвижные друг относительно друга массы газа (v₂—1>1 = 0), сжатые до различных давлений. Действи­тельно, из всех четырех случаев, изображенных на рис. 78, только во втором из них газы 1 я 2 движутся в одинаковом направлении и потому может быть v\ = v₂.

Далее, в третьем случае (Н-+Р+ТР+) в обе стороны от тангенциального разрыва распространяются по волне разре­жения. Если газы 1 я 2 разлетаются друг от друга с достаточно большой скоростью v₂ — fi, то в волнах разрежения давление может достичь при своем падении значения нуль. Тогда возни­кает картина, изображенная на рис. 78, г; между областями 4 и 4' образуется область вакуума 3.

Выведем аналитические условия, определяющие характер распада начального разрыва в зависимости от его параметров. Будем считать во всех случаях, что р₂ > Рь а положительное направление оси х выбираем везде в направлении от области / к области 2 (в соответствии с рис. 78).

Имея в виду, что газы по обеим сторонам начального раз­рыва могут быть газами различных веществ, будем различать их, называя соответственно газами 1 я 2.

1. Распад Н -* У+ТУ+. Если р₃ = р₃, v₃=v'₃, V₃, V₃ — давле­ние, скорость и удельные объемы в образовавшихся после распада областях 3 и 3', то имеем р₃ > р₂ > рь а объемы V₃ и V₃ определяются как абсциссы точек с ординатами р₃ на ударных адиабатах, проведенных соответственно через точки Pi, Vi и рг, V2 в качестве исходных. Поскольку газы в областях 3 и 3' в выбранной системе координат неподвижны, то согласно формуле (85,7) можно написать для скоростей v\ и v₂, направ­ленных соответственно в положительном и отрицательном на­правлениях оси х:

Щ = л/(Рз — - V_a), v₂= — V(/>3- Рг) (V₃ - Vi).

Наименьшее значение, которое может иметь давление р₃ при за­данных pi и р₂ так, чтобы не противоречить исходному предпо­ложению (р₃ > р₂ > pi), есть р₃ = р₂. Имея также в виду, что разность vi — v₂ есть монотонно возрастающая функция р₃, на­ходим искомое неравенство

vi-v₂> V(p₂-p,)(K,-n. (100,1)

где посредством V обозначен объем, являющийся абсциссой точки с ординатой р₂ на ударной адиабате газа 1, проведенной через точку pi, Vi в качестве начальной. Вычислив V по фор­муле (89,1) (написав в ней V вместо V₂), получим для поли­тропного газа условие (100,1) в виде

». - v_s > (р₂ - Р.) д/==Ж=1 • (100,2)

Отметим, что условия (100,1—2), устанавливающие границу воз­можных значений разности скоростей vi —v₂, не зависят, оче­видно, от выбора системы координат.

2. Распад Н —* Здесь р, < р₃ = р'₃< р₂. Для ско-

рости газа в области 1 имеем опять:

0| = У(Рз~ Pi) (Vi — V^,

а полное изменение скорости в волне разрежения 4 равно со­гласно (99,7)

^u2= § У— dpdV.

Pj

При заданных pi и р₂ значения р₃ могут лежать в пределах от pi до рг. Заменяя р₃ в разности и₂ — t>i один раз на р_ь а дру­гой — на р₂, получим условие

Рг

-5 ^J-dpdV<vi-v₂<V(P2-P.)(^i-V"). (ЮО.З)

Здесь V" имеет тот же смысл, что и в предыдущем случае; вы­ражение, определяющее верхний предел разности vi — v₂, долж­но вычисляться для газа /, а нижний предел — для газа 2. Для политропного газа получим:

<~^Pl)Л/<*-ор.+'<?,+ор»• <¹⁰⁰'⁴⁾

где с₂ = д/^Рг^г^— скорость звука в газе 2 в состоянии

3. Распад Я Р ч- ГР -к Здесь _р.₂ > р, > р₃ = р₃ > 0. Тем же путем найдем следующее условие осуществления этого случая:

Pi Pi Pi

-jj«J—dpdV-j^J-dpdV<i>, -v₂<—<j-yf-dpdV.

^{0 0}»* (100,5)

Интеграл в правой стороне неравенства вычисляется для газа 2, а в левой стороне первый интеграл — для газа /, а второй — для газа 2. Для политропного газа получим:

Г Ys-l

2С[ 2с₂

Yi — 1 y2 — 1

_<0l__0j<_^[l ₍Ю0,6)

где с, = Vyi/⁷^!, ^с2 = Vy2P2^2- Если

то между волнами разрежения возникает область вакуума (рас­пад Н-+Р<-ВР-+).

К задаче о разрыве в начальных условиях сводятся, в ча­стности, задачи о различных столкновениях плоских поверхно­стей разрывов. В момент столкновения обе плоскости совпадают и представляют собой некоторый «начальный разрыв», в даль­нейшем распадающийся одним из описанных выше способов. Так, в результате столкновения двух ударных волн снова возни­кают две ударные же волны, расходящиеся от остающегося между ними тангенциального разрыва:

Когда одна ударная волна догоняет другую, возможны два слу­чая:

У+У+-+У+ТУ+, У+У+-+Р+ТУ+.

В обоих случаях вперед продолжает распространяться ударная же волна.

К этой же категории относится задача об отражении и про­хождении ударной волны через тангенциальный разрыв (гра­ницу двух сред). Здесь возможны два случая:

У+Т-+У+ТУ+, У+Т-+Р+ТУ+.

Прошедшая во вторую среду волна всегда является ударной (см. также задачи к этому параграфу)¹).

') Для полноты упомянем, что при столкновении ударной волны со сла­бым разрывом (эта задача не относится к рассматриваемому здесь автомо­дельному типу) ударная волна продолжает распространяться в прежнем направлении, а в пространстве позади нее остается один слабый разрыв пер­воначального типа и один «тангенциальный» (см конец § 96) слабый разрыв.

Задачи

1. Плоская ударная волна отражается от плоской поверхности абсолют-
но твердого тела. Определить давление газа позади отраженной волны.
(Я. Hugoniot, 1885).

Решение. В результате падения ударной волны на твердую стенку возникает отраженная ударная волна, распространяющаяся от стенки. Будем отмечать индексами 1, 2, 3 соответственно невозмущенный газ перед падаю­щей ударной волной, газ позади падгющей волны (он же является газом впереди отраженной волны) и газ позади отраженной волны (рис. 79; стрелками показано направление движения ударных волн и самого газа). Газ в граничащих с твердой стенкой областях / и 3 покоится (относительно не­подвижной стенки). Поэтому относительная скорость газов по обе стороны разрыва друг относительно друга в обоих случаях — в падающей и отраженной ударных волнах — одинакова (равна одной и той же величине — скорости газа 2). Воспользовавшись формулой (85,7) для относи­тельной скорости, получим поэтому:

(р* - Pi) (Vi - V,) = (рз - р₂) (V* - V,).

•I

Уравнение же ударной адиабаты (89,1) для каждой из ударных волн дает

v± (у + Op.+ (v- Dp*

Рис. 79

V, " (Y-J)Pi + (Y+ DPi ' Уз ^ (Y+ 1)P2 + (V— 1)Рз V₂ (Y-1)P2+(Y+l)/>s '

Из этих трех уравнений можно исключить удельные объемы, в результате чего получается:

(Рз - р₂)² [(Y + 1) pi + (V - 1) Pal = (Р* - Pi)² l(Y + О Р» + (Y - О РЛ-

Это есть квадратное уравнение для рз, имеющее тривиальный корень pj = p_t; после сокращения на (рз — pi) получим искомую формулу

Рз ₌ (Зу— 1)р₂ —(Y— l)pi р₂ (Y—1)р2+(Y+l)Pi '

определяющую рз по pi и р₂. В предельном случае большой интенсивности падающей волны «досжатие» газа отраженной ударной волной определяется формулами

Рз Зу — 1 Уз _ У — 1
Р2 Y — 1 ' Vi у '

В обратном предельном случае малой интенсивности: р₃ — р₂ = р₂ — pi, что соответствует звуковому приближению.

2. Найти условие, определяющее результат отражения ударной волны от
плоской границы между двумя газами.

Решение. Пусть Pi=p₂, V_х, V₂ — давления и удельные объемы обеих сред до падения ударной волны (распространяющейся в газе 2) на их поверх­ность раздела, а рг, У г — давление и удельный объем позади ударной волны. Условие того, чтобы отраженная волна была ударной, определяется неравен­ством (100,2), в котором надо в данном случае положить

Выражая все величины через отношение давлений pa/pi и начальные удельные объемы V[ и V₂, получим следующее условие:

__________ V_x К

(Yi + 1) Р2/Р1 + (Yi — 1) (Y2 + 1) Рг/Pi + (Y2 — i) '

§ 101. Одномерные бегущие волны

При изучении звуковых волн в § 64 амплитуда колебаний в волне предполагалась малой. В результате уравнения движе­ния оказывались линейными и могли быть легко решены. Ре­шением этих уравнений является, в частности, функция от ж± ct (плоская волна), что соответствует бегущей волне с про­филем, перемещающимся со скоростью с без изменения своей формы (под профилем волны понимают распределение различ­ных величин — плотности, скорости и' т. п. — вдоль направления ее распространения). Поскольку скорость v, плотность р и дав­ление р (как и другие величины) в такой волне являются функ­циями от одной и той же комбинации х ± ct, то они могут быть выражены как функции друг от друга в виде соотношений, не содержащих явно ни координаты, ни времени (например, р = = р(р), v — v(p) и т. д.).

В случае произвольной, не малой, амплитуды волны эти про­стые соотношения уже не имеют места. Оказывается, однако, возможным найти общее решение точных уравнений движения, представляющее собой бегущую плоскую волну и являющееся обобщением решения f(x±ct) приближенных уравнений, при­менимых в случае малых амплитуд. Для отыскания этого реше­ния будем исходить из требования, чтобы в общем случае вол­ны с произвольной амплитудой плотность и скорость могли быть выражены в виде функции друг от друга.

При отсутствии ударных волн движение адиабатично. Если в некоторый начальный момент времени газ был однороден (так что, в частности, было s = const), то и в дальнейшем будет все время s = const, что и предполагается ниже; тогда и давление будет функцией только от плотности.

В плоской звуковой волне, распространяющейся вдоль оси х, все величины зависят только от дг и г, а для скорости имеем v_x = v, v_v = v_z = 0. Уравнение непрерывности гласит:

dp, d{pv) ___п ~ЬТ~^Х'~ЪЧ ^и'

а уравнение Эйлера

Воспользовавшись тем, что у может быть представлено в виде функции только от р, напишем эти уравнения в виде

£+-Т£-°- <¹⁰¹''>

ж + (»+Ш£=°- <^10|'²>

Замечая, что

др/дх \dt)_р'

получаем из (101,1)

\dt)_p— dp^ — ^{v + 9} dp •

а из (101,2) аналогично

(4r). —+ffc- <""'³>

Но поскольку значение p определяет однозначным образом зна­чение v, то безразлично, берется ли производная при постоян­ном р или v, так что

(~зг)р⁼⁼("дтХ'

откуда

dv _1_ dp с² dp

Р dp р dv р da '

Таким образом, dv/dp = ±с/р, откуда

_{и = ±}^_{р = ±}$|Р_. (Ю1,4)

Этим определяется общая связь между скоростью и плотностью или давлением в волне¹).

Далее, комбинируя (101,3) с (101,4), пишем:

(*).-»+7*-^±«<"-

или, интегрируя,

x = t[v±c(v)] + f(v), (101,5)

где f(v)—произвольная функция скорости, а функция c(v) опре­деляется равенством (101,4).

Формулы (101,4—5) представляют собой искомое общее ре­шение (впервые найденное Риманом — В. Riemann, 1860). Ука-

') В волне с малой амплитудой имеем р = р₀ + р', и (101,4) дает в пер­вом приближении i> == Сор'/ро (где Со=с(р₀)), т.е. обычную формулу (64,12), занные формулы определяют неявным образом скорость (а с нею и остальные величины) как функцию от х и /, т. е. профиль волны в каждый момент времени. Для каждого определенного значения v имеем х = at + b, т. е. точка, в которой скорость имеет определенное значение, передвигается в пространстве с постоянной скоростью; в этом смысле найденное решение пред­ставляет собой бегущую волну. Два знака в (101,5) соответ­ствуют волнам, распространяющимся (относительно газа) в по­ложительном и отрицательном направлениях оси х.

Движение, описываемое решением (101,4—5) часто назы­вают простой волной; ниже мы будем пользоваться этим терми­ном. Изученное в § 99 автомодельное движение является част­ным случаем простой волны, соответствующим равной нулю функции f(v) в (101,5).

Дата добавления: 2014-11-07