Ol — V2X 55 страница

ТТ—pT-J+T' -77-7+Г7Г- ⁽⁸⁹'^10>

Отношение T₂/Ti неограниченно растет вместе с р₂/р\, т. е. ска-
чок температуры, как и скачок'давления, в ударной волне мо-
жет быть сколь угодно большим. Отношение же плотностей
стремится к постоянному пределу; так, для одноатомного газа
предельное значение р₂ = 4р_ь для двухатомного р₂ = брь Ско-
рости распространения ударной волны большой интенсивности
равны ___________ ___________ _____________

⁰^ ⁼ V'¹T^lp2Fl• ^VacT+i')^¹- ^(89,И>

Они растут пропорционально корню из давления р₂.

M,-l = l-M₂ = ^-_Z> ±i-=l+J^J__z,

Наконец, приведем соотношения для ударных волн слабой интенсивности, представляющие собой первые члены разложе­ний по степеням малого отношения г = (р₂— Р\)/р\-

v±l_z> £i._{= 1+}rzl
4v ci 2у

Pi Y 2Y² \ • /

Здесь сохранены члены, дающие первую поправку к значениям, отвечающим звуковому приближению.

Задачи

1. Получить формулу

где с» — критическая скорость (L. Prandtl).

Решение. Поскольку величина ш + и²/2 непрерывна на ударной волне, можно ввести критическую скорость, одинаковую для газов 1 \\ 2 согласно-

YPi,», УР2 v\ у + 1

-------- + -7Г = ТТ.--------- ГГГ- + -ST" = -------------------- ГГ- с

(Y-1) р, 2 <_Y_l)p₂ ' 2 2 (y-1)

(cp. (83,7)). Определяя из этих равенств р₂/р₂ и р₄/р, и подставляя их в-уравнение

о, — v₂ = — Si—

^{1 2} Р2»2 Pl»l (результат комбинирования (85,1) и (85,2)), получим

Y+1 / с² \

—я— (»1 - о₂) I 1 --) = 0.

2у \ v,v₇ /

- Ввиду того что t>i Ф с₂, отсюда следует искомое соотношение.

2. Определить отношение p₂/pi по заданным температурам Ti, Т_г для ударной волны в термодинамически идеальном газе с непостоянной тепло­емкостью.

Решение. Для такого газа можно лишь утверждать, что w (как и е) есть функция только от температуры и что р, V, Т связаны уравнением со­стояния pV = RT/\i. Решая уравнение (85,9) относительно р%1р\, получаем:

где Wi -- w(Ti), w₂ — w(T₂).

§ 90. Гофрировочная неустойчивость ударных волн

Соблюдение условий эволюционности само по себе необхо­димо, но еще недостаточно для гарантирования устойчивости ударной волны. Волна может оказаться неустойчивой по отно­шению к возмущениям, характеризующимся периодичностью вдоль поверхности разрыва и представляющим собой как бы «рябь», или «гофрировку», на этой поверхности (такого рода возмущения рассматривались уже в § 29 для тангенциальных разрывов)¹). Покажем, каким образом исследуется этот вопрос для ударных волн в произвольной среде (С. П. Дьяков, 1954).

Пусть ударная волна покоится, занимая плоскость х = 0; жидкость движется сквозь нее слева направо, в положительном направлении оси х. Пусть поверхность разрыва испытывает воз­мущение, при котором ее точки смещаются вдоль оси х на ма­лую величину

C = C₀e'(V-»')_f (90,1)

где k_y — волновой вектор «ряби». Эта рябь на поверхности вы­зывает возмущение течения позади ударной волны, в области х > 0 (течение же перед разрывом, х < 0, не испытывает воз­мущения в силу своей сверхзвуковой скорости).

Произвольное возмущение течения складывается из энтро­пийно-вихревой волны и звуковой волны (см. задачу к § 82). В обоих зависимость величин от времени и координат дается множителем вида ехр [г (кг — ы()] с той же частотой со, что и в (90,1). Из соображений симметрии очевидно, что волновой век­тор к лежит в плоскости ху; его «/-компонента совпадает с k_y в (90,1), а х-компонента различна для возмущений двух типов.

*) Неустойчивость по отношению к таким возмущениям называют гофри-ровочной (corrugation instability по английской терминологии).

В энтропийно-вихревой волне kv₂ = со, т. е. kx = со/у₂ («2 — невозмущенная скорость газа за разрывом). В этой волне воз­мущение давления отсутствует, возмущение удельного объема связано с возмущением энтропии, 6У^(ЭНТ) = (dV/ds)_p8s, а возму-

щение скорости подчинено условию

k 6v<^9HT»=— oo«»"» + k,dv\J^m)=0. (90,2)

В звуковой волне в движущемся газе связь между частотой и волновым вектором дается равенством (ш — kv)² —с²й² (см. (68,1)); поэтому k_x в этой волне определяется уравнением

(«-W=^cK*x+ **,)• (90,3)

Возмущения давления, удельного объема и скорости связаны со­отношениями:

бр(зв)₌₌_(_С2/1/₂)2₀т/(з_В)₍ (9_0>4)

(ю — v₂k_x) 6v^(3B> - V₂k6p<³*\ (90,5)

Возмущение в целом представляется линейной комбинацией возмущений обоих типов:

So = 6о<^энт> + 6о^(зв>, 6V = 6У^(ЭНТ> + 6V'^3B>, 6р = 6р^,зв>. (90,6)

Оно должно удовлетворять определенным граничным условиям на возмущенной поверхности разрыва.

Прежде всего, на этой поверхности должна быть непрерывна тангенциальная к ней со­ставляющая скорости, а скачок нормальной составляющей должен выражаться через воз­мущенные давление и плотность равенством (85,7). Эти условия записываются как

v₁t = (v₂ + 6v)t, v,n — (v₂ + 6v) n =

= [(p₂-p_i + bp)(v_i-v₂-6v)}⁴²,

где t и n — единичные векторы касательной
и нормали к поверхности разрыва (рис. 59).
С точностью до величин первого порядка ма-
лости компоненты этих векторов (в плоско- р_ис. 59
сти ху) равны t((££, 1) и п(1,— ikt,); выраже-
ние iki возникает как производная dt,/dy. С этой же точностью
граничные условия для скорости принимают вид

to, = to,~^[^-^]. (90,7)

Далее, возмущенные значения р₂ + Ьр и У₂ + 6У₂ должны удовлетворять тому же уравнению адиабаты Гюгонио, что и не­возмущенные р₂ и V₂. Отсюда получаем условие, связывающее Ър и 6V:

⁶Р = Ж^ЬУ> <⁹⁰>⁸>

где производная берется вдоль адиабаты.

Наконец, еще одно соотношение возникает из связи между потоком вещества через поверхность разрыва и скачками дав­ления и плотности на ней. Для невозмущенного разрыва это со­отношение выражается формулой (85,6), а для возмущенного аналогичное соотношение есть

1 / \2 Рг — Р\ + бр

—я- (V^ — Un)² = — ^{Н1 и},

V² V_l-V₂-6V

где u — скорость точек поверхности разрыва. В первом прибли­жении по малым величинам имеем un = —г'ю£; разлагая напи­санное равенство также и по степеням бр и 6V, получим:

2to_g== бр ЬУ

Равенства (90,2), (90,4—5), (90,7—9) составляют систему восьми линейных алгебраических уравнений для восьми вели­чин £, бр, 6У<^ЭНТ>, 6К^(ЗВ), бо^»,. 6v^_y '). Условие совместности этих уравнений (выражаемое равенством нулю определителя их коэффициентов) имеет вид:

²-f +7) " (£+*«)^(ffl - ^{(| + k)} ~°' ^№,0)

где для краткости обозначено h = ^(dVi/dpi), а / имеет обыч­ный смысл: / = Vi/Vi = V2/V2. Величину к_х в (90,10) надо пони­мать как функцию k_y и со, определяемую равенством (90,3).

Условие неустойчивости состоит в существовании возмуще­ний, экспоненциально возрастающих со временем, причем они должны экспоненциально убывать с удалением от поверхности разрыва (т. е. при х-*со); последнее условие означает, что ис­точником возмущения является сама ударная волна, а не ка­кой-то внешний по отношению к ней источник. Другими сло­вами, волна неустойчива, если уравнение (90,10) имеет решения, у которых

1ти>0, Im k_x>0. (90,11)

') Все эти равенства берутся при х =*= 0, и под перечисленными величи­нами в них могут подразумеваться постоянные амплитуды, без переменных экспоненциальных множителей. ²) Это исследование можно найти в оригинальной статье: Дьяков С. П.— ЖЭТФ, 1954, т. 27, с. 288. В следующем параграфе будет приведено еще и менее строгое, но более наглядное обоснование условий (90,12—13),

Исследование уравнения (90,10) на предмет выяснения усло­вий существования таких решений довольно громоздко. Мы не будем производить его здесь, ограничившись указанием оконча­тельного результата²). Гофрировочная неустойчивость ударной

f^<-l, (90,12)

волны возникает если

;2

dp₂

или

напомним, что производная берется вдоль ударной адиабаты (при заданных р_и Vi) ¹).

Условия (90,12—13) отвечают наличию у уравнения (90,10) комплексных корней, удовлетворяющих требованиям (90,11).Но в определенных условиях это уравнение может иметь также и корни с вещественными со и k_x, отвечающие «уходящим» от раз­рыва реальным незатухающим звуковым и энтропийным вол­нам, т. е. спонтанному излучению звука поверхностью разрыва. Мы будем говорить о такой ситуации как об особом виде не­устойчивости ударной волны, хотя неустойчивости в буквальном смысле здесь нет, — раз созданное на поверхности разрыва воз­мущение (рябь) неограниченно долго продолжает излучать волны, не затухая и не усиливаясь при этом; энергия, уносимая излучаемыми волнами, черпается из всей движущейся среды²).

Для определения условий возникновения этого явления, пре­образуем уравнение (90,10), введя угол 0 между к и осью Jtj тогда

cJk_x = со₀ cos 0, c₀k„ = щ sin 0, <о = со₀ (1 + — cos 9),

«о = ct (kl + ky)

(«о — частота звука в системе координат, движущейся вместе с газом за ударной волной), и получаем квадратное относитель­но cosO уравнение:

-5 г

(1+^)=0. (90,13)

') Отметим, что при выводе (90,12—13) используется только обязатель­ное условие (88,1), но не используется неравенство p%> pi. Поэтому эти условия неустойчивости относятся и к ударным волнам разрежения, которые могли бы существовать при (d²V/dp²)_s < 0. ²) Сравните с аналогичной ситуацией для тангенциальных разрывов — задача 2 § 84.

Скорость распространения звуковой волны в движущемся со скоростью v₂ газе, по отношению к неподвижной поверхности разрыва, есть t/₂-f-c₂cos 0. Звуковая волна будет уходящей, если эта сумма положительна, т. е. если

— v₂/c₂ < cos 8 < 1 (90,16)

(значения cos0<0 отвечают случаям, когда вектор к направ­лен в сторону разрыва, но снос звуковой волны движущимся га­зом делает ее все же «уходящей»). Спонтанное излучение звука ударной волной возникает, если уравнение (90,15) имеет ко­рень, лежащий в этих пределах. Простое исследование приводит к следующим неравенствам, определяющим область этой не­устойчивости '):

1 — v\lc\ — v,vJc\ „ dVo о»

²'1 - < /»—i < 1 + 2-1 (90,17)

1 — v₂/c₂ + v_Kv₂jc₂ dp₂ c₂

(нижний и верхний пределы здесь фактически отвечают ниж­нему и верхнему пределам в условиях (90,16)). Область (90,17) примыкает к области неустойчивости (90,13), расширяя ее.

¹) Эта неустойчивость тоже была указана С. П. Дьяковым (1954); пра­вильное значение нижней границы в (90,17) найдено В. М. Конторовичем (1957).

К происхождению неустойчивости ударных волн в области (90,17) можно подойти также и с несколько иной точки зрения, рассмотрев отражение от поверхности разрыва звука, падаю­щего на нее со стороны сжатого газа. Поскольку ударная волна движется относительно газа впереди нее со сверхзвуковой ско­ростью, то в этот газ звук не проникает. В газе же позади вол­ны будем иметь, наряду с падающей звуковой волной, еще и от­раженную звуковую и энтропийно-вихревую волны (а на самой поверхности разрыва возникает рябь). Задача об определении коэффициента отражения по своей постановке близка к задаче об исследовании устойчивости. Разница состоит в том, что на­ряду с подлежащими определению амплитудами исходящих от разрыва (отраженных) волн в граничных условиях фигурирует еще и заданная амплитуда приходящей (падающей) звуковой волны. Вместо системы однородных алгебраических уравнений мы будем иметь теперь систему неоднородных уравнений, в ко­торых роль неоднородности играют члены с амплитудой па­дающей волны. Решение этой системы дается выражениями, в знаменателях которых стоит определитель однородных уравне­ний,— как раз тот, приравнивание которого нулю дает диспер­сионное уравнение спонтанных возмущений (90,10). Тот факт, что в области (90,17) это уравнение имеет вещественные корни для cos 0, означает, что существуют определенные значения угла отражения (и тем самым угла падения), при которых коэф­фициент отражения становится бесконечным. Это — другая фор­мулировка возможности спонтанного излучения звука, т. е. из­лучения без падающей извне звуковой волны.

То же самое относится и к коэффициенту прохождения зву­ка, падающего на поверхность разрыва спереди, навстречу ей. В этом случае не существует отраженной волны, а позади по­верхности разрыва возникают прошедшие звуковая и энтропий­но-вихревая волны. В области (90,17) возможно обращение коэффициента прохождения в бесконечность¹).

Скажем несколько слов о некоторых возможных, в прин­ципе, типах ударных адиабат, содержащих области рассмотрен­ных неустойчивостей²).

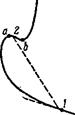
Условие (90,12) требует отрицательной производной dptjdV^, причем ударная адиабата должна быть наклонена (к оси абсцисс) в точке 2 менее круто, чем проведенная в нее хорда 12 (т. е. обратно тому, что имеет место в обычных случаях — рис. 53). Для этого адиабата должна перегнуться, как показано на рис. 60; условие неустойчивости (90,12) выполняется на уча­стке ab.

\Р

V 1

Рис. 60

Рис. 61

') Вычисление коэффициентов отражения и прохождения звука на удар­ной волне при произвольных направлениях падения в произвольных средах — см. Дьяков С. П. — ЖЭТФ, 1957, т. 33, с. 948, 962; Конторович В. М.—ЖЭТФ, 1957, т. 33, с. 1527; Акустический журнал, 1959, т. 5, с. 314. ²) В политропном газе h = —(C[/t)i)², в чем легко убедиться с помощью полученных в § 89 формул. Ни одно из условий (90,12—13) и (90,17) при этом заведомо не выполняется, так что ударная волна устойчива. Устойчивы, конечно, также и ударные волны слабой интенсивности в произвольной среде.

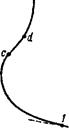
Условие (90,13) требует положительности производной dpi/dVi, причем наклон адиабаты должен быть достаточно мал. На рис. 60 это условие выполняется на определенных отрезках адиабаты, непосредственно примыкающих к точкам а и Л и рас­ширяющих, таким образом, область неустойчивости. Условие (90,13) может оказаться выполненным и на участке (cd на рис. 61) адиабаты, не содержащей участка типа аЪ.

Условие (90,17) еще менее жестко, чем (90,13) и еще допол­нительно расширяет область неустойчивости на адиабатах Гю-гонио с dp₂/dV₂ > 0. Более того, нижний предел в (90,17) мо­жет быть отрицательным, так что неустойчивость этого типа мо­жет, в принципе, иметь место и в некоторых участках адиабат обычного вида, со всюду отрицательной производной dp₂/dV₂.

Вопрос о судьбе гофрировочно-неустойчивых ударных волн тесно связан со,следующим замечательным обстоятельством: при выполнении условий (90,12) или (90,13) решение гидродинами­ческих уравнений оказывается неоднозначным (С. S. Gardner, 1963). Для двух состояний среды, 1 я 2, связанных друг с дру­гом соотношениями (85,1—3), ударная волна является обычно единственным решением задачи (одномерной) о течении, пере­водящем среду из состояния / в 2. Оказывается, что если в со­стоянии 2 выполнены условия (90,12) или (90,13), то решение указанной гидродинамической задачи не однозначно: переход из состояния 1 в 2 может быть осуществлен не только в ударной волне, но и через более сложную систему волн. Это второе ре­шение (его можно назвать распадным) состоит из ударной волны меньшей интенсивности, следующего за ней контактного разрыва и из изэнтропической нестационарной волны разреже­ния (см. ниже § 99), распространяющейся (относительно газа позади ударной волны) в противоположном направлении; в ударной волне энтропия увеличивается от s\ до некоторого зна­чения s₃ < s₂, а дальнейшее увеличение от S3 до заданного s₂ происходит скачком в контактном разрыве (эта картина отно­сится к типу, изображенному ниже на рис. 78, б; предполагается выполненным неравенство (86,2))').

Вопрос о том, чем определяется отбор одного из двух реше­ний в конкретных гидродинамических задачах, не ясен. Если отбирается распадное решение, то это означало бы, что неустой­чивость ударной волны с самопроизвольным усилением поверх­ностной ряби вообще не осуществляется. По-видимому, однако, такой отбор не может быть связан именно с этой неустойчи­востью, поскольку неоднозначность решения не ограничена ус­ловиями (90,12—13) ²).

Задачи

•) В статье Gardner С. S. — Phys. Fluids, 1963, v. 6, p. 1366 это пока­зано для области (90,13). Более общее рассмотрение, включающее и область (90,12), дано Кузнецовым Н. М. —- ЖЭТФ, 1985, т. 88, с. 470; там же рас­смотрены ударные адиабаты с нарушением условия (<Э^гУ/с5р²)₅ > 0, когда распадные решения складываются из других совокупностей волн. ²) По-видимому, область неоднозначности простирается на ударной адиабате несколько за пределы области неустойчивости, определяемой этими условиями. См, об этом указанную выше статью Н. М. Кузнецова,

1. На ударную волну падает сзади (со стороны сжатого газа) нормально к ней плоская звуковая волна. Определить коэффициент отражения звука.

Решение. Рассматриваем процесс в системе координат, в которой удар­ная волна покоится, а газ движется через нее в положительном направлении оси х; падающая звуковая волна распространяется в отрицательном направ­лении оси х. При нормальном падении (а потому и отражении) в отражен­ной энтропийной волне скорость 6v^(3HI) = 0. Возмущение давления: бр = = 6р^(зв) + 6р⁽⁰⁾, где индекс (0) относится к падающей, а индекс (зв) — к отраженной звуковым волнам. Для скорости 8v_x = 8v имеем

6₀=-^-(бр^(зв> -6р<°>)

(разность вместо суммы возникает ввиду противоположных направлений рас­пространения обоих волн). Второе из граничных условий (90,7) имеет преж­ний вид (но в нем теперь 6V = 6V<°> + 6К<³⁸> + 6V<³">); с учетом (90,8) и формулы (85,6) переписываем его как

_5o = _-L=i^-(6p<-> +бр<°>).

(1)

Приравняв друг другу оба выражения 6у, получим для искомого отношения амплитуд давления в отраженной и падающей звуковых волнах:

6р^(зв) 1 — 2М₂ — h

бр⁽⁰> 1 + 2М_? - h

(где М₂ = v₂/с₂). Оно обращается в бесконечность на верхней границе об­ласти (90,17)

Для политропного газа h = — Mj~². При слабой интенсивности ударной волны (р₂— pi < pi) отношение (1) стремится к нулю как (р% — рО², а в обратном случае большой интенсивности стремится к постоянному пределу

6р^(зв>Уу - Уд (y - о

6р<°> ~ Уу" + V2 (y - о '

2. На ударную волну падает спереди, нормально к ней, плоская звуковая волна. Определить коэффициент прохождения звука').

Решение. Возмущение в газе / перед ударной волной

6p,=6p⁽⁰>. 6V,=6V^,0> =--^-6p,, bv^^-bpu а в газе 2 позади нее:

6р₂ = бр'^зв), 6У₂ = 6V^(3B> + 6V^(3HT), 6о₂ = -^-др₂

(индексы (0), (зв), (энт) относятся к падающей звуковой и к прошедшим

звуковой и энтропийным волнам). Возмущения бр₂ и 6V₂ связаны друг с

другом соотношением, следующим из уравнения ударной адиабаты: если
последнее выражено в виде V₂ = V₂(p₂; Pi, V0, то

') Для политропного газа эта задача рассматривалась Д. И. Блохинце-вым (1945) и Бюргерсом (/. М. Burgers, 1946).

■(^b⁺[-T©,^t(?)J'"

(индекс Н у производных указывает, что они берутся вдоль адиабаты Гю-гонио¹)). Граничное условие (90,7) заменяется теперь на

2 L р₂ — Pi к 1 — V₂ J

⁼ ~ тг^[6p? ~^6р> ~^{jl (flfj} ~^6v,)1-

Приравняв два выражения для ба₂ — 6i»i, получим для искомого отношения амплитуд в прошедшей и падающей звуковых волнах:

(2)

6р^(зв) (1 + М,)² + <?

6р^<й) 1 + 2М₂ — h

L с² VdV,/_H Чф, /Д

где h имеет прежнее значение, а 9 = У"

Для политропного газа

Y-1 (М?-1)²

<7 = — „

Y + 1 М²

и коэффициент прохождения:

6р^(зв)(1+М,)²

6р^<0) 1 4- 2М₂

+ м,-²[ Y + iv м,;J

При слабой интенсивности ударной волны отсюда получается

а в обратном случае большой интенсивности:

«Р^Ьв) „ 1 р₂

бр⁽⁰⁾ Y+V2v(V-l) Pi

В обоих случаях амплитуда давления в прошедшей звуковой волне возра­стает по сравнению с давлением в падающей волне.

§ 91. Распространение ударной волны по трубе

Рассмотрим распространение ударной волны по среде, за­полняющей длинную трубку с переменным сечением. Наша цель состоит при этом в выяснении влияния, оказываемого измене­нием площади ударной волны на ее скорость (G. В. Whitham, 1958).

') Производная (<ЭУ₂/<Зр₂)«есть то, что мы обозначали выше просто как dV₂/dp₂, подразумевая, что производная берется при постоянных р,, Vi.

Будем считать, что площадь S(x) сечения трубки лишь мед­ленно меняется вдоль ее длины (ось я) — мало на расстояниях порядка ширины трубки. Это дает возможность применить при­ближение (его называют гидравлическим), которое уже было использовано в § 77: можно считать все величины в потоке постоянными вдоль каждого поперечного сечения трубки, а ско­рость— направленной вдоль ее оси; другими словами, течение рассматривается как квазиодномерное. Такое течение описывает­ся уравнениями

ж + °£ + т%г=°- <»и>

*+•£-«'($+»£)=<>■ <⁹'.2>

Первое из них — уравнение Эйлера, второе — уравнение адиаба-тичности, а третье — уравнение непрерывности, представленное в виде (77,1).

Для выяснения интересующего нас вопроса достаточно рас­смотреть трубку, в которой изменение площади S(x) не только медленно, но и по абсолютной величине остается относительно малым на протяжении всей длины. Тогда будут малы и связан­ные с непостоянством сечения возмущения потока, и уравнения (91,1—3) могут быть линеаризованы. Наконец, должны быть по­ставлены начальные условия, исключающие появление каких-либо посторонних возмущений, которые могли бы повлиять на движение ударной волны; нас интересуют только возмущения, связанные с изменением S(x). Эта цель будет достигнута, если принять, что ударная волна первоначально движется с постоян­ной скоростью по трубе постоянного сечения, и площадь сечения начинает меняться только вправо от некоторой точки (которую примем за х — 0).

Линеаризованные уравнения (91,1—3) имеют вид

dt ' дх р дх dbp. дбр 2 (дбр,, <Э6р dt + ^V дх

дбр. дбр, dbv. pv d6S _п

-дТ + '^,-дГ+Р-дГ + ^£8--дГ = ⁰'

где буквы без индекса обозначают постоянные значения вели­чин в однородном потоке в однородной части трубки, а сим­вол б обозначает изменение этих величин в трубке переменного сечения. Умножив первое и третье из этих уравнений соответ­ственно на рс и с² и сложив затем все три уравнения, напишем следующую их комбинацию:

+ + *4с-](*Р + = - ^ ^- (91,4)

Общее решение этого уравнения дается суммой общего решения однородного уравнения и частного решения уравнения с правой частью. Первое есть F(x— vt — ct), где F— произвольная функ­ция; оно описывает звуковые возмущения, приходящие слева. Но в однородной области, при х < 0, возмущений нет; поэтому надо положить F = 0. Таким образом, решение сводится к ин­тегралу неоднородного уравнения:

6p + _Pc8v = --^^-. (91,5)

Ударная волна движется слева направо со скоростью v\ > С\ по неподвижной среде с заданными значениями р_ь р_;. Движе­ние же среды позади ударной волны (среда 2) определяется ре­шением (91,5) во всей области трубки слева от точки, достиг­нутой разрывом к данному моменту времени. После прохожде­ния волны все величины в каждом сечении трубки остаются по­стоянными во времени, т. е. равными тем значениям, которые qhh получили в момент прохождения разрыва: давление р₂, плот­ность р₂ и скорость vi — v₂ (в соответствии с принятыми в этой главе обозначениями, v% обозначает скорость газа относительно движущейся ударной волны; скорость же его относительно сте­нок трубки есть тогда v\— v₂). В этих обозначениях (и снова выделив переменные части этих величин) равенство (91,5) запи­шем в виде

Ц. =, _ »«-°» + * _{{Ьр2 + р2С2 (б0} _ _ft0 у}. ₍₉1 _>6)

S P₂(^i-f₂)c₂

Все величины 8vi, 6i>₂, бр₂ можно выразить через одну из них, например, 6ui. Для этого пишем варьированные соотношения (85,1—2) на разрыве (при заданных р, и pi):

р^о, = v₂6o₂ + p₂6v₂, 2/ (во, - 6v₂) = Ьр₂ + v\bp₂

(где / = p\V\ — р₂и₂ — невозмущенное значение потока); к ним надо еще присоединить соотношение

S 6fi Vic₂ где снова введено обозначение

где производная берется вдоль адиабаты Гюгонио. Вычисление приводит к следующему окончательному соотношению, связы­вающему изменение bv\ скорости ударной волны относительно неподвижного газа перед ней, с изменением 8S площади сечения трубки:

1 6S Pi — Р_г + е₂ Г 1 +2t)₂/c₂ — h-\

1 Г+А j' ⁽⁹¹'⁷⁾

Коэффициент при квадратной скобке в (91,7) положителен. Поэтому знак отношения 8vi/8S определяется знаком выраже­ния в этой скобке. Для всех устойчивых ударных волн этот знак положителен, так что ovi/oS < 0. Но при выполнении ка­кого-либо из условий (90,12—13) гофрировоч-ной неустойчивости выражение в скобках стано­вится отрицательным, так что 8v\/oS > 0.

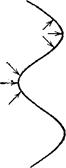
Этот результат дает возможность наглядного истолкования происхождения неустойчивости. На рис. 62 изображена «гофрированная» поверх­ность ударной волны, перемещающаяся напра­во; стрелками схематически показано направле­ние линий тока. При перемещении ударной волны на выдавшихся вперед участках поверх­ности площадь 6S растет, а на отставших участ­ках— уменьшается. При 6i>i/6S < 0 это приво­дит к замедлению выступивших участков и ускорению отставших, так что поверхность стре- Рас. 62 мится сгладиться. Напротив, при 8vi/8S > 0 воз­мущение формы поверхности будет усиливаться: выступающие участки будут уходить все дальше, а отставшие — все более отставать').

Дата добавления: 2014-11-07