Должно быть 8 страница

В предыдущем параграфе мы рассмотрели частный случай сверхзвукового стационарного двухмерного течения (простую волну), характерный тем, что в нем величина скорости является функцией только ее направления: у = и(9). Это решение не могло бы быть получено из уравнения Чаплыгина; для него тож­дественно 1/ДэО, и оно теряется, когда при преобразовании к плоскости годографа приходится умножать уравнение движения (уравнение непрерывности) на якобиан А. Положение здесь аналогично тому, что мы имели в теории одномерного нестацио­нарного движения. Все сказанное в § 105 о взаимоотношении ме­жду простой волной и общим интегралом уравнения (105,2) пол­ностью относится и ко взаимоотношению между стационарной простой волной и общим интегралом уравнения Чаплыгина.

Положительность якобиана А при дозвуковом движении по­зволяет установить определенное правило, относящееся к направ­лению поворота скорости вдоль потока (А. А. Никольский, Г. И. Таганов, 1946). Имеем тождественно

_1_ _ д (6, о) ^ д (9, у) д (х, о) Л — д(х, у) д(х, у) д(х, у)'

или

4--(£).($).- <"•.««

В дозвуковом потоке А > 0, и мы видим, что производные (д0/ох)_о и (dv/dy)_x имеют одинаковый знак. Этот результат имеет простой геометрический смысл: если передвигаться вдоль линии v = const = vo так, чтобы область v <С v₀ лежала справа, то угол 9 будет монотонно возрастать, т. е. вектор скорости монотонно поворачивается против часовой стрелки. Этот ре­зультат относится, в частности, и к линии перехода из до- В сверхзвуковое течение, вдоль которой v = с = с»,

В заключение выпишем уравнение Чаплыгина для политроп-" ного газа выразив в нем в явном виде с через v.

1 _ V ~ * "²

д²Ф, ₂ Y+l ct д²Ф. дФ _п,,,„,,4

-ШГ+v²-------------------- —jjt— -W + "-to=0. (П6,П)

Это уравнение обладает семейством частных интегралов, выра­жающихся через гипергеометрические функции¹).

§ 117. Характеристики плоского стационарного течения

Некоторые общие свойства характеристик плоского стацио­нарного (сверхзвукового) движения были рассмотрены уже в § 82. Выведем теперь уравнения, определяющие эти линии по за­данному решению уравнений движения.

В плоском стационарном сверхзвуковом потоке имеется в общем случае три семейства характеристик. По двум из них (которые мы будем называть характеристиками С₊ и С_) рас­пространяются все малые возмущения, за исключением лишь возмущений энетропии и ротора скорости; последние распро­страняются по характеристикам третьего семейства Со, совпа­дающим с линиями тока. Для заданного течения линии тока из­вестны, и вопрос заключается в определении характеристик пер­вых двух семейств.

Направления проходящих через каждую точку плоскости ха­рактеристик С₊ и С_ расположены по обе стороны от проходя­щей через ту же точку линии тока и образуют с ней угол, рав­ный местному значению угла возмущений а (рис. 51). Обозна­чим посредством то тангенс угла наклона к оси (угловой коэф­фициент) линии тока в данной ее точке, а посредством т+ и т- — угловые коэффициенты характеристик С₊ и С_. Тогда по формуле сложения тангенсов напишем:

1 + m₀m₊ *£^а> j m_Qm_ ^T£^a>

откуда

± 1 =F m₀ tg a

(верхние знаки относятся везде к С+, а нижние — к С_). Под­ставив сюда

V С

т₀ = —, tga:

*) См., например, Седов Л. И. Плоские задачи гидродинамики и аэроди­намики. — М.: Наука, 1966, гл. X; Мизсс Р. Математическая теория течений сжимаемой жидкости. — М.: ИЛ, 1961, § 20.

² — <

и. произведя сокращения, получим следующее выражение для угловых коэффициентов характеристик:

(117,1)

Если распределение скоростей в потоке известно, то это есть дифференциальное уравнение, определяющее характеристики С₊ и. С-¹).

Наряду с характеристиками в плоскости х, у можно рас­сматривать также и характеристики в плоскости годографа, в особенности полезные при изучении изэнтропического потенци­ального течения, о котором мы и будем ниже говорить. С мате­матической точки зрения это — характеристики уравнения Чап­лыгина (116,8) (принадлежащего при v>c к гиперболиче­скому типу). Следуя известному из математической физики об­щему методу (см. § 103), с помощью коэффициентов этого урав­нения составляем уравнение характеристик:

dv² + dQ²

или

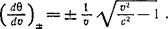
Определяемые этим уравнением характеристики не зависят от конкретного решения уравнения Чаплыгина, что связано с неза­висимостью коэффициентов последнего от Ф. Характеристики в плоскости годографа, являющиеся отображением характеристик С+ и С_ в физической плоскости, мы будем условно называть соответственно характеристиками Г+ и Г- (знаки в (117,2) со­ответствуют этому условию).

') Уравнение (117,1) определяет характеристики и для стационарного осесимметрического течения, если только заменить v_y и у на v_r и г, где г — цилиндрическая координата (расстояние от оси симметрии — оси х); ясно, что весь вывод не изменится, если вместо плоскости х, у рассматривать про­ходящую через ось симметрии плоскость х, т.

Интегрирование уравнения (117,2) дает соотношения вида J+(v, 0) = const, /_(и,6) = const. Функции /₊ и /_ представляют собой величины, остающиеся постоянными соответственно вдоль характеристик С₊ и С_ (инварианты Римана). Для политропного газа уравнение (117,2) может быть проинтегрировано в явном виде. Нет, однако, необходимости производить эти вычисления заново, так как результат может быть написан заранее с по­мощью формул (115,3—4). Действительно, согласно общим свой­ствам простых волн (см. §. 104) зависимость о от 0 в простой волне как раз и определяется условием постоянства во всем про­

странстве одного из инвариантов Римана. Произвольной по­стоянной в формулах (115,3) и (115,4) является ср*; исключая из этих формул параметр ср, получим:

arc sin

О -i) -________________________

Характеристики в плоскости годографа представляют собой се­мейство эпициклоид, заполняю­щих пространство между двумя ^vy окружностями радиусов (рис. 117):

V = с* и

Для изэнтропического потен­циального движения характери­стики Г+, Г_ обладают следую­щим важным свойством: семей­ства характеристик Г+ и Г_ орто­гональны соответственно характе­ристикам С- и С₊ (предполагает­ся, что оси координат х, у изобра­жены параллельными осям v_x,

Для доказательства этого утверждения исходим из уравнения (114,3) для потенциала плоского течения, имеющего вид

дхду ду²

:0

(117,4)

(существенно, что в нем отсутствует свободный член).

Угловые коэффициенты т± характеристик С± определяются как корни квадратного уравнения

Ат² — 2Вт + С = 0.

Рассмотрим выражение dv+ dx~ + dv+ dy~, в котором дифференциалы скорости берутся вдоль характеристики Г+, а дифференциалы координат — вдоль С_. Имеем тождественно:

-j- dx⁺ dx

-J^-(dx+ dy~ +dx-dy⁺) + -0-dy+ dy~.

dv+ dx~ + dv+ dy~ =

⁴) Это утверждение не относится к характеристикам осесимметрического движения в плоскости х, г\

_ d²g> ~ дх²

Разделив это выражение на dx+dx~, получим в качестве коэффи­циентов при д²у/дхду и д²у/ду² соответственно т+ + т~ = 2BIA и т+т- = С/А, после чего ясно, что в силу уравнения (117,4) выражение обращается в нуль. Таким образом,

dv + dx~ + dv+ dy~ = dv⁺ dr~ = 0. Аналогично получим:

dv~dr+ = 0.

Эти равенства и выражают собой сделанное выше утверждение.

§ 118. Уравнение Эйлера — Трикоми. Переход через звуковую скорость

Существенный принципиальный интерес имеет исследование особенностей течения, возникающих при переходе из до- в сверх­звуковую область, или обратно. Стационарные течения, сопро­вождающиеся таким переходом, называются смешанными или трансзвуковыми, а самую границу перехода называют переход­ной или звуковой поверхностью.

Для исследования течения вблизи границы перехода в осо­бенности удобно уравнение Чаплыгина, сильно упрощающееся в этой области.

На границе перехода v = с = с», а вблизи нее (в околозвуко­вой области) разности v — с» и с — с* малы и связаны друг с другом соотношением (114,8):

Произведем соответствующие упрощения в уравнении Чаплы­гина. Третий член уравнения (116,8) мал по сравнению со вто­рым, содержащим 1 — v²/c² в знаменателе. Во втором же члене полагаем приближенно

2 2

v с:

1 - v²/c² 2(1- v/c) 2а» (1 - с/с.) '

Наконец, вводя вместо скорости v новую переменную

П = (2а*)^1/3-^рЧ (118,1)

получим искомое уравнение в виде

д²Ф д²Ф _п та о\

•) К рассматриваемой газодинамической проблеме уравнение Трикоми было привлечено Ф. И. Франклем (1945).

Уравнение такого вида в математической физике называется уравнением Эйлера — Трикоми '). В полуплоскости г\ > 0 оно от-

носится к гиперболическому, а в полуплоскости г) < 0 — к эл­липтическому типу. Мы рассмотрим здесь ряд чисто математи­ческих свойств этого уравнения, которые существенны для иссле­дования тех или иных конкретных физических случаев.

Характеристики уравнения (118,2) определяются уравнением

имеющим общий интеграл:

е±4_чз,²=с,

(118,3)

где С — произвольная постоянная. Это уравнение изображает в плоскости Tj, 0 два семейства характеристик, представляющих собой ветви полукубических парабол, расположенных в правой полуплоскости с точками возврата на оси 9 (рис. 118).

дФ у = ж

При исследовании движения в не­большой области пространства, в ко­торой направление скорости газа меня­ется незначительно¹), всегда можно выбрать направление оси х так, чтобы отсчитываемый от нее угол 0 во всей рассматриваемой области был малым. Тогда сильно упрощаются также и уравнения (116,6), определяющие ко­ординаты х, у по функции Ф(г|,0)²):

* = (2а*)^1/3^-,

Для того чтобы избежать появления в формулах лишнего мно­жителя (2а*)^1/3, мы будем ниже, в §§ 118—121, пользоваться вместо координаты х величиной х(2а^)-¹^, обозначая ее той же буквой х. Тогда

х —

(118,4)

²) Мы опустили в правых сторонах равенства множители 1/с»; это озна­чает лишь замену функции Ф на с*Ф, не меняющую уравнения (118,2) н потому всегда допустимую.

Полезно заметить, что ввиду такой простой связи с Ф функ­ция у(ц,Щ (но не х(г|,0)) тоже удовлетворяет уравнению Эйле­ра — Трикоми. Имея это в виду, можно написать якобиан пре­образования из физической плоскости в плоскость годографа в виде

* - TWTW = «* " ^ф-^ф» - Ш' - ч (*)" ■ <¹¹⁸'⁵>

Как уже сказано, уравнение Эйлера — Трикоми приходится обычно применять для исследования свойств решения в окре­стности начала координат в плоскости ц, 0. В физически интерес­ных случаях эта точка представляет собой особую точку реше­ния. В связи с этим особое значение приобретает семейство ча­стных интегралов уравнения Эйлера — Трикоми, обладающих определенными свойствами однородности. Именно, речь идет о решениях, однородных по отношению к переменным 0² и ту³; та­кие решения должны существовать, поскольку преобразование 0²->-а0², г|³->аг|³ оставляет инвариантным уравнение (118,2). Будем искать эти решения в виде

o>=e²V(i), 1=1

где k — постоянная (степень однородности функции Ф по отно­шению к указанному преобразованию). Переменную £ мы вы­брали такой, что она обращается в нуль на характеристиках, проходящих через точку п = 0 = 0. Сделав подстановку, полу­чим для функции /(£) уравнение

6(1- |)Г + [|-2Л2*)]f/ = 0.

Это — частный случай гипергеометрического уравнения. С по­мощью известного выражения для двух независимых интегралов гипергеометрического уравнения находим искомое решение (при нецелом числе 2k + 1/6) в виде

+ в('-#Г"''(*+т *+f»+*'-*)]• <»м>

С помощью известных соотношений между гипергеометрически­ми функциями от аргументов г, у, 1 —z, _{ ^_, _; ^_ _z молено

представить это решение еще в пяти других видах; при исследо­вании различных конкретных случаев приходится пользоваться всеми этими видами '). Мы приведем здесь лишь следующие два

') Соответствующие формулы можно найти, например, в §е Математи­ческого приложения в III. Пользуемся случаем исправить опечатку в формуле (е, 9) этого параграфа: во втором члене должен стоять множитель г"~Ч (вместо 2^a_y).

вида:

4_ 4t|³ \1 3 ¹ 99² ЛГ

(118,7)

99² 4t|³

) +

В

„3/2

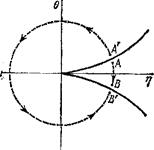
(118,8)

(постоянные Л, В в формулах (118,6—8), конечно, не совпа­дают). Из этих выражений сразу следует важное свойство функ­ций Ф/й, не видное непосредственно из выражения (118,6): линии т] = 0 и 0 = 0 не являются их особыми линиями (из (118,7) видно, что вблизи и = 0 Ф*. разлагается по целым степеням rj, а из (118,8) — то же самое по 0). Из выражения же (118,6) видно, что характеристики, напротив, являются особыми ли­ниями общего (т. е. содержащего обе постоянные А и В) одно­родного интеграла Ф* уравнения Эйлера — Трикоми: при неце­лом 2/2+1/6 точками разветвления обладает множитель (99² — 4n³)^2ft+1/б, а при целом 2/е + 1/6 один из членов в (118,6) вообще теряет смысл ') (либо при 2k + 1/6 = 0 совпадает с дру­гим) и должен быть заменен вторым независимым решением гипергеометрического уравнения, имеющим, как известно, в этом случае логарифмическую особенность.

Между интегралами Ф& с различ­ными значениями k имеются следую­щие соотношения:

(118,10)

Ф_к = Ф__й__1/6(90² - 4п³)²*^+1/6, (118,9)

Ф*-1/2 =

Первое следует непосредственно из
выражения (118,6), а второе — из того,
что функция дф/г/д0 удовлетворяет
уравнению Эйлера — Трикоми и имеет Рис 119

ту же степень однородности, что и

Ф*-1/2. В этих формулах под ф_к подразумевается, конечно, об­щее выражение с двумя произвольными постоянными.

*) Напомним, что ряд F(a, р\ у; г) при у = 0, —1, —2,... теряет смысл.

При исследовании решения в окрестности точки т) = 0 = 0 приходится следить за его изменением при обходе вокруг этой точки. Пусть, например, функция ф_к (118,6) изображает реше­ние в точке А вблизи характеристики 0 = ²/₃т]^3/2 (рис. 119) н требуется найти форму решения вблизи характеристики 0 =

= —²/зЦ^3/2 (в точке В). Переход вдоль АВ связан с пересече­нием оси абсцисс; между тем значение 0 = 0 есть особая точка гипергеометрических функций в выражении (118,6), так как их аргумент обращается в бесконечность. Поэтому для совершения перехода необходимо сначала применить к гипергеометрическим функциям преобразование, переводящее их в функции обратного

(

99² \ эег _ _4т)з j • Д^ля которых 0 = 0 уже не будет особой

точкой, после чего меняем знак 9 и повторным таким же преоб­разованием переводим их в функции прежнего аргумента. Та­ким способом получим для функций, входящих в выражение (118,6), следующие формулы преобразования:

г(-2*-^г(-2^+|Л

2sinnl

+Г(-2*)г(-2* + -|)

2 sin j

Fa _______ 2**+'/³ v 67 V 6 7

я(26 + 1) ' r(2fe+l)r(2fe + y)

причем под f 1 и f₂ подразумеваются выражения

С- loi»ll i!!!J²*^+1/6pCb-I_ ¹ fc-J_² 9fe-I_⁷-1 ^4l?\

(118,11)

(118,12)

в которых 0 и 1—4т]³/90² в коэффициентах при гипергеометри­ческих функциях берутся по их абсолютным значениям.

Аналогичным образом можно получить формулы преобразо­вания при переходе из точки А' в точку В' (рис. 119) путем обхода начала координат в обратном направлении. Вычисления при этом более громоздки, так как приходится проходить через три особые точки гипергеометрических функций — точку с 0 = О и два раза точки с п = 0 (напомним, что особыми точками ги­пергеометрической функции аргумента г являются точки z = 1 и 2=00). Окончательные формулы гласят:

sin я f 4* — 4-|

л-------)—&i +

sin я (2* + -g- J

+ F_a ■ 2-**⁺²>³ cos п (2k + 1) -i------------------- ^{ь) V} "Л

^{4 ЬУ} Г (-2ft) Г (-2*-г—)

§1191 РЕШЕНИЕ УРАВНЕНИЯ ЭЙЛЕРА —ТРИКОМИ 619

rin*(4*-i-)

^{V 6;} (118,13)

+ Т⁷! • 2 cos

„₍₂,₊.₎^г("Н)Ф₊|)

^0/ Г(2&+1)Г(2а+^)

Наряду с рассмотренным семейством однородных решений можно построить, конечно, и другие семейства частных интегра­лов уравнения Эйлера — Трикоми. Укажем здесь семейство ре­шений, возникающих в связи с разложением Фурье по углу 9. Если искать Ф в виде

®_v=gA4)e^±M, (118,14)

где v — произвольная постоянная, то для функции g_v получим уравнение

Это — уравнение функций Эйри; его общий интеграл есть

iM^-V^M/Tr]³'²). ^(И8,15)

где Zi/з — произвольная линейная комбинация функций Бесселя порядка Уз-

Наконец, полезно иметь в виду, что общий интеграл уравне­ния Эйлера — Трикоми может быть написан в виде

G)=\f(Qdz, $ = 2³-3т}г + 39, (118,16)

с

где f(t,)—произвольная функция, а интегрирование производит­ся в плоскости комплексного переменного z по любому контуру С, на концах которого производная /'(£) принимает одинаковые значения. Действительно, непосредственная подстановка выраже­ния (118,16) в уравнение дает

^-^ = s\(z'-4)f"®dz = 3\f^Qdr,==3f'(Ol==0, с

т. е. уравнение удовлетворяется.

§ 119. Решения уравнения Эйлера — Трикоми вблизи неособых точек звуковой поверхности

Выясним теперь, какие решения соответствуют тем слу­чаям, когда в окрестности границы перехода течение газа не об­ладает никакими физическими особенностями (нет слабых раз­рывов или ударных волн). Для этого, однако, удобнее исходить не непосредственно из уравнения Эйлера — Трикоми, а из урав­нения для потенциала скорости в физической плоскости. Такое уравнение было выведено в § 114; для плоского движения урав­нение (114,10) после введения новой координаты согласно х х (2а*)1^1/3 принимает вид

д_Ф д²ср __ 6"ф _{]Q п}

дх дх² ~~ ду^{2 1} U'w.iJ

Напомним, что потенциал ф определен здесь таким образом, что его производные по координатам дают скорость согласно равен­ствам

f.=„, f-e. (над

Заметим также, что уравнение Эйлера — Трикоми можно полу­чить и непосредственно из уравнения (119,1), переходя к незави­симым переменным 0, т] с помощью преобразования Лежандра, причем будет Ф = — ф + хц + уд, или

_{ф =} _Ф _{+ ч}™_+в™. (119,3)

Выбрав начало координат х, у в точке звуковой линии, ок­рестность которой мы исследуем, разложим ф по степеням х и у. В общем случае первый член разложения, удовлетворяющего уравнению (119,1), есть

<f = ~xy. (119,4)

При этом 9 = х/а, и = у/а, так что

Ф = а9т). (119,5)

По степени однородности этой функции ясно, что ему соответ­ствует одна из функций Ф5/6; это есть второй член выражения (118,7), в котором гипергеометрическая функция с k — ⁵/₆ сво­дится просто к 1;

Если мы хотим найти уравнение звуковой линии в физической плоскости, то написанный первый член разложения недостаточен. Следующий член разложения Ф имеет степень однородности 1, т. е. соответствует одной из функций Ф1; это есть первый член выражения (118,7), сводящийся при k=l к полиному:

Таким образом, первые два члена разложения Ф: Ф = а_ч0 + й (е² + х)-

Отсюда

х = aQ + bif, у = ац + 2bQ.

(119,6) (119,7)

Звуковая линия (ti = 0) есть прямая у = 2Ьх/а.

Для нахождения же уравнения характеристик в физической плоскости достаточен первый член разложения. Подставляя Q = x/a, ц = у/а в уравнение годографических характеристик G = ±2г)^3/2/3> получим:

,3/2

3-\/а

т. е. снова две ветви полукубической параболы с точкой возврата на звуковой линии (жирная кривая на рис. 120).

Это свойство характеристик заранее оче- линия тока ^

видно из следующих простых соображе- ^{4 л}

ний. В точках линии перехода угол Маха равен я/2. Это значит, что касательные к характеристикам обоих семейств совпадают, что и означает наличие здесь точки возвра­та (рис. 120). Линии же тока пересекают звуковую линию перпендикулярно к харак­теристикам, не имея здесь особенностей.

Решение (119,6) неприменимо в том ис­ключительном случае, когда линия тока пер­пендикулярна к звуковой линии в рассмат­риваемой точке¹). Вблизи такой точки те­чение, очевидно, симметрично относительно оси х. Этот случай требует особого рассмотрения (Ф. И. Франкль и С. В. Фалькович, 1945).

Симметрия течения означает, что при изменении знака у ско­рость v_y меняет знак, a v_x остается неизменной. Другими сло­вами, потенциал ср должен быть четной функцией у (а потен­циал Ф — четной функцией 0). Первые члены разложения ср бу­дут поэтому в этом случае иметь следующий вид:

(П9,8)

(относительный порядок малости х и у не предопределен, так что все три написанных члена могут быть одинакового поряд­ка). Отсюда находим следующие формулы преобразования из

*) В решении (119,6) этому соответствовало бы равенство нулю постоян­ной а; но при а = 0 это решение теряет смысл, так как на линии rj == 0 обращается в нуль якобиан Д.

физической плоскости в плоскость годографа:

_п = ах + ^£-, Q = a²xy + ^f-. (119,9)

Уже не решая этих уравнений относительно х п у в явном виде, легко видеть, что степень однородности функции t/(9, tj) равна ¹/в. Поэтому соответствующая функция Ф имеет k = ^l/_s -f '/₂ = = ²/₃, т. е. заключена в общем интеграле Ф2/3.

Иключив из уравнений (119,9) х, получим для определения функции y(Q, Tj) кубическое уравнение

(ау)³ — З_ча# + 3е = 0. (119,10)

При в² — 4г|³/9 > 0, т. е. во всей области слева от годографи-ческих характеристик, проходящих через точку г\ = 6 = 0 (в том

У

Рис 121

числе во всей дозвуковой области, т) <; 0; рис. 121), это урав­нение имеет всего один вещественный корень, который и дол­жен быть взят в качестве функции y(Q,я). В области же справа от характеристик вещественны все три корня; из них должен быть взят тот, который является продолжением вещественного в левой области корня.

Характеристики в физической плоскости (проходящие через начало координат) получаются подстановкой выражений (119,9) в уравнение 4tj³ = 99². Это дает две параболы:

характеристики 23 и 56: х = — ауЩ,
характеристики 34 и 45: х = 01^/2 (119,11)

(цифры указывают, какие две области в физической плоскости разделяет данная характеристика). Звуковая же линия (т) = 0 в плоскости годографа) в физической плоскости есть парабола х = —ау²/2 (жирная кривая на рис. 121). Отметим следующую особенность точки пересечения звуковой линии с осью симметрии* из этой точки -^исходят четыре ветви характеристик, между тем как из всякой другой точки звуковой линии — всего две.

На рис. 121 одинаковыми цифрами отмечены соответствую­щие друг другу области плоскости годографа и физической пло­скости. Это соответствие — не взаимно однозначное¹); при пол­ном обходе вокруг начала координат в физической плоскости об­ласть между двумя характеристиками в плоскости годографа проходится трижды, как это указано пунктирной линией на рис. 121 дважды отражающейся от характеристик.

Поскольку функция y(Q, и) сама удовлетворяет уравнению Эй­лера — Трикоми, то она должна содержаться в общем интеграле Ф1/₆. Вблизи характеристики 23 в физической плоскости это есть

1 /Зву/Зр/ 1 1 1. 4if\ /но ю\
^ = 7Г1Т\) ^F{~T' У Т' <¹¹⁹'¹²⁾

(первый член выражения (118,6), не имеющий особенности на характеристике). Производя ее аналитическое продолжение в окрестность характеристики 56 (по пути, проходящему через дозвуковую область /, т. е. с помощью формул (118,13)), мы получим там такую же функцию. Вблизи же характеристик 34 и 45 y(Q, г\) представится линейными комбинациями этой функ­ции и функции

""VS^T-f-i"-*) <"ЗД

(второй член выражения (118,6)); эти комбинации получаются путем аналитического продолжения с помощью формул (118,11) (причем надо иметь в виду, что при каждом отражении от го-дографической характеристики квадратный корень в функции (119,13) меняет знак).

С математической точки зрения полученные результаты пока-вывают, что функции Ф1/6 являются линейными комбинациями корней кубического уравнения

/³ — Зг]/ + 3е = 0, (119,14)

т. е. сводятся к алгебраическим функциям ²). Вместе с Ф1/6 сво­дятся к алгебраическим функциям также и все Ф* с

А-=4±у, я-0, 1, 2,.... (119,15)

⁴) В соответствии с тем, что на характеристике х = ау²12 в физической плоскости имеем Д = оо (см. примечание на стр. 609).

^s) Пользоваться явным выражением этих функций, получаемым из (119,14) с помощью формулы Кардана, фактически неудобно.

получающиеся согласно формулам (118,9) и (118,10) из (Di/₆ пу­тем последовательных дифференцирований (Ф. И. Франкль, 1947).

К алгебраическим функциям сводятся также те функции с

(119,16)

в которых гипергеометрическая функция сводится к полиному¹) (так, при k = п/2 это есть первый член, а при k = —п/2 — вто­рой член выражения (118,6)).

К этим трем семействам алгебраических функций Ф_к отно­сятся, в частности, все те функции, которые могут соответство­вать (в качестве потенциала Ф) течениям, не имеющим ника­ких особенностей в физической плоскости. Именно, для таких течений все члены разложения Ф вблизи несимметричной точки линии перехода (первые два члена которого даются формулой (119,6)) могут иметь лишь k = 5/6 -4- п/2 или k = 1 + п/2. Раз­ложение же Ф вблизи симметричной точки (начинающееся чле­ном с А = 2/3) может, кроме того, содержать еще функции с k = 2/3 + п/2.

Дата добавления: 2014-11-07