Тема 2. Элементы дифференциального исчисления

А (-3; 9), B (6; - 3), С(11; 7).

А (-5;11), B (4; - 1), С(9; 9).

А (-5; 6), B (4; - 6), С(9; 4).

А (-4; 12), B (5; 0), С(10; 10).

А (-3; 9), B (6; - 3), С(11; 7).

А (-6; 11), B (3; - 1), С(8; 9).

А (-10; 12), B (-1; 0), С(4; 10).

А (-2; 13), B (7; 1), С(12; 11).

А (-1; 3), B (8; - 9), С(13; 1).

А (1; 4), B (10; - 8), С(15; 2).

ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ

В задачах 1-10 даны координаты вершин треугольника ABC. Требуется:

1) найти длину стороны AB;

2) составить уравнения сторон AB и BC;

3) вычислить угол при вершине А;

4) составить уравнение высоты CE;

5) найти длину высоты CE.

Подставляя в уравнение (2) координаты точек А и В, находим уравнение стороны АВ

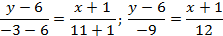
Отсюда

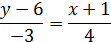
Или

После простейших преобразований получаем

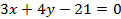(3)

Уравнение вида

называется общим уравнением прямой на плоскости. От него нетрудно перейти к уравнению прямой с угловым коэффициентом:

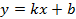
Разрешим уравнение (3) относительно переменной y, в результате чего получим

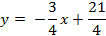
Это уравнение стороны AB с угловым коэффициентом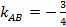

Подставляя теперь в (2) координаты точек A и С, получим уравнение стороны AC сначала в общем виде, а затем в виде уравнения прямой с угловым коэффициентом:

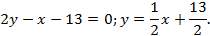
Угловой коэффициент прямой AC равен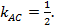

1) Если даны две прямые, угловые коэффициенты которых и 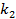то тангенс угла 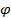между ними вычисляется по формуле

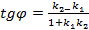(4)

Для определение угла A используем угловые коэффициенты прямых AB и АС: 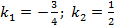. Отсюда по формуле (4)

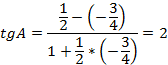
Теперь найдем сам угол:

2) Высота CE перпендикулярна стороне AB. Известно, что если две прямые взаимно перпендикулярны, то их угловые коэффициенты 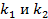удовлетворяют условию

(5)

Поэтому 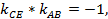откуда

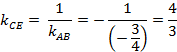
Уравнение прямой, проходящей через заданную точку и имеющий заданный угловой коэффициент 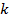, имеет вид

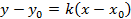(6)

Подставляя в уравнение (6) координаты точки C и значение углового коэффициента , получаем уравнение высоты CE:

Для определения длины высоты CE найдем координаты точки E – точки пересечения высоты CE и стороны AB. С этой целью решим систему уравнений, составленную из уравнений прямых CE и AB:

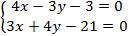(7)

Умножая первое уравнение системы (7) на (4), а второе – на (3) и складывая результаты получим 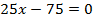, то есть 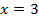. Теперь нетрудно найти y из любого уравнения системы (7): 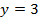. Таким образом, координаты точки E найдены: E(3;3). Отсюда по формуле (1) вычисляем длину высоты CE:

C

Треугольник ABC и высота СЕ построены в системе ко­ординат хОу на рис. 1.

Рис. 1

В этой теме основное внимание должно быть уделено ус­воению понятия функции, предела функции, непрерывности и, наконец, важнейшему в математическом анализе понятию производной.

Следует тщательно разобраться в вопросах использова­ния аппарата дифференциального исчисления при исследо­вании поведения функции и построении ее графика.

Дата добавления: 2014-10-15