Динамическая теорема Кориолиса

ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ

ЗАКОНЫ СВОБОДНОГО ПАДЕНИЯ ГАЛИЛЕЯ

Рассмотрим свободное падение тела в пустоте (вакууме).

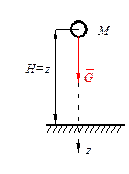
Тело находится над поверхностью земли на расстоянии H, не имея начальной скорости. Тогда дифференциальное уравнение движения в проекции на ось Z:

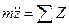(проекция сил на ось Z)

т.е.

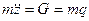
или

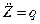
Интегрируя полученное выражение, получаем:

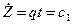c=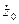=V_м=0 (начальная скорость)

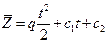с₁= z₀=0 (м) начальная координата

т.к. z=H то:

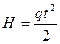(1)

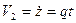(2)

Уравнения (1) и (2) выражает законы свободного падения Галилея.

Из (1) очевидно:

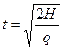- время свободного падения не содержит массы, поэтому в вакууме все тела в независимости от массы имеют одинаковое время падение.

ПРИНЦИП ОТНОСИТЕЛЬНОЙ КЛАССИЧЕСКОЙ МЕХАНИКИ ГАЛИЛЕЯ

До сих пор мы рассматривали движение несвободной точки по отношению к неподвижной инерциальной системе отсчета, в которой законы динамики выполняются с достаточной точностью, а также система связана с Землей, которую условно считают неподвижной.

Рассмотрим теперь движение несвободной точки по отношению к подвижной системы отсчета и установим основное уравнение динамики относительного движения несвободной материальной точки.

Пусть P – заданная сила, N - динамическая реакция связи. Координаты точки в подвижной системе - 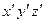. По теореме Кориолиса:

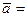
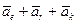
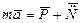(1)

Если рассмотрим движение точки в подвижной системе, то, как известно из кинематики, точка будет находиться в сложном движении, и если движение подвижной системы не будет поступательным, то ускорение 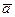по теореме Кориолиса (абсолютное ускорение) будет представляться

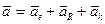(2),

Подставим уравнение (2) в (1) и, так как нас интересует динамика относительного движения, то в левой части уравнения (1) оставим

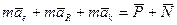
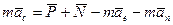
Обозначим: - 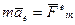переносная сила инерции

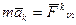- кориолисова сила инерции

Тогда дифференциальное уравнение относительного движения запишется:

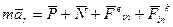(3)

Таким образом, отмечаем в случае непоступательного переносного движения подвижной системы отсчета относительное движение точки происходит также, как и абсолютное (в соответствии с 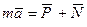) и плюс переносная и кориолисова силы инерций.

Причем: инерционные силы не являются результатом воздействия других тел на точку, а являются следствием наличия движения системы отсчета 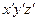, которая сообщает точке переносное и кориолисово ускорение, которое в свою очередь провоцируют появление сил инерции.

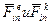
Формула (3) выражает динамическую теорему Кориолиса.

Дата добавления: 2014-10-15