
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема. Границя функції в точці та на проміжку. Властивості границь. Неперервність функції в точці та на проміжку. Властивості неперервних функцій
|
|
|
|
План
- Границя функції в точці та на проміжку.
- Властивості границь.
- Неперервність функції в точці та на проміжку.
- Властивості неперервних функцій.
1. Поняття границі функції в точці.
Нехай задано деяку функцію, наприклад, f(x) = 2х – 1. Розглянемо графік цієї функції та таблицю її значень у точках, які на числовій прямій розташовані достатньо близько до числа 2.
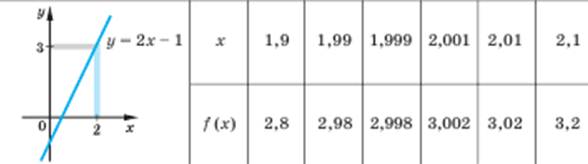 |
З таблиці та графіка видно, що чим ближче аргумент х до числа 2 (це позначають х  2 і кажуть, що х прямує до 2), тим ближче значення функції f(x) = 2х – 1 до числа 3 (позначають f(x)
2 і кажуть, що х прямує до 2), тим ближче значення функції f(x) = 2х – 1 до числа 3 (позначають f(x)  3 і кажуть, що f(x) прямує до 3). Це записують також так:
3 і кажуть, що f(x) прямує до 3). Це записують також так:  (2х – 1) = 3 (читається: «Ліміт 2х – 1 при х, що прямує до 2, дорівнює 3» і кажуть, що границя функції 2х – 1 при х, що прямує до 2 (або границя функції в точці 2), дорівнює 3.
(2х – 1) = 3 (читається: «Ліміт 2х – 1 при х, що прямує до 2, дорівнює 3» і кажуть, що границя функції 2х – 1 при х, що прямує до 2 (або границя функції в точці 2), дорівнює 3.
У загальному випадку запис  означає, що при
означає, що при 
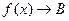 , тобто В – число, до якого прямує значення функції f(x), коли х прямує до а.
, тобто В – число, до якого прямує значення функції f(x), коли х прямує до а.
Запис позначень  і
і 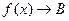 за допомогою знака модуля
за допомогою знака модуля
| Позначення і його зміст | Ілюстрації | Запис за допомогою модуля |
 На числовій прямій точка ч знаходиться від точки а на малій відстані (менше
На числовій прямій точка ч знаходиться від точки а на малій відстані (менше  ) )
| 
| 
|
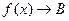 Значення
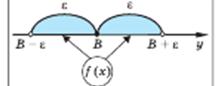
Значення  на числовій прямій знаходиться на малій відстані від В (менше на числовій прямій знаходиться на малій відстані від В (менше 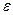 ) )
| 
| 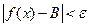
|
| Означення границі функції в точці | ||

| Число В називається границею функції f(x) у точці а ( при х, що прямує до а), якщо для будь-якого додатного числа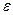 знайдеться таке додатне число знайдеться таке додатне число  , що при всіх х , що при всіх х а, які задовольняють нерівності а, які задовольняють нерівності  , виконується нерівність , виконується нерівність 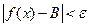
|
2. Властивості границь
| Зміст правил граничного переходу | Запис і формулювання правил граничного переходу |
Якщо f(x) = c, то при  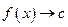
|  Границя сталої функції дорівнює цій самій сталій
Границя сталої функції дорівнює цій самій сталій
|
Якщо при 
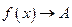 і і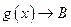 , то , то 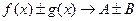
| 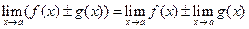 Границя суми (різниці) двох функцій дорівнює сумі (різниці) їх границь, якщо границі доданків існують
Границя суми (різниці) двох функцій дорівнює сумі (різниці) їх границь, якщо границі доданків існують
|
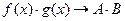
| 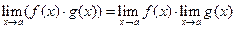 Границя добутку двох функцій дорівнює добутку їх границь, якщо границі множників існують
Границя добутку двох функцій дорівнює добутку їх границь, якщо границі множників існують
|

|  Сталий множник можна виносити за знак границі
Сталий множник можна виносити за знак границі
|
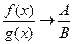 (де В (де В  0) 0)
|  (де (де 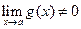 )
Границя частки двох функцій дорівнює частці їх границь, якщо границі чисельника і знаменника існують і границя знаменника не дорівнює нулю )
Границя частки двох функцій дорівнює частці їх границь, якщо границі чисельника і знаменника існують і границя знаменника не дорівнює нулю
|
3. Неперервність функції в точці та на проміжку
Функція f(x) називається неперервною в точці а, якщо при 
 , тобто
, тобто

4. Властивості неперервних функцій
Якщо функція f(x) неперервна в кожній точці деякого проміжку І, то її називають неперервною на проміжку І.
Якщо функції f(x) і g(x) неперервні в точці а, то сума, добуток і частка неперервних в точці а функцій неперервні в точці а (частка у випадку, коли дільник g(x) 0)
0)
Графік функції, неперервної на проміжку, - нерозривна лінія на цьому проміжку.
Всі елементарні функції неперервні в кожній точці своєї області визначення, тому на кожному проміжку з області визначення їх графіки – нерозривні лінії.
Якщо на інтервалі  функція f(x) неперервна і не перетворюється на нуль, то вона на цьому інтервалі зберігає сталий знак.
функція f(x) неперервна і не перетворюється на нуль, то вона на цьому інтервалі зберігає сталий знак.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 888; Нарушение авторских прав?; Мы поможем в написании вашей работы!