
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема. Похідні елементарних функцій . Правила диференціювання функцій
|
|
|
|
Вправи
- Розкрити зміст нерівності
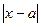 <
< .
. - Як зобразити
 - околицю точки а = - 2, якщо
- околицю точки а = - 2, якщо  = 0,5.
= 0,5. - Розв'язати рівняння та нерівності:
1) 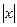 = 4;
= 4;
2) 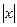 = 0;
= 0;
3) 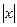 = -6;
= -6;
4) 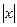 = х;
= х;
5) 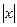 = - х;
= - х;
6) 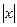 > 0;
> 0;
7) 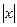 < 0;
< 0;
8) 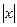
 2;
2;
9) 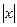 > 7;
> 7;
10) 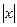
 -5.
-5.
- Чи є неперервною в кожній із точок х = -1, х = 1, х = 3 функція, графік якої зображено на рис 1
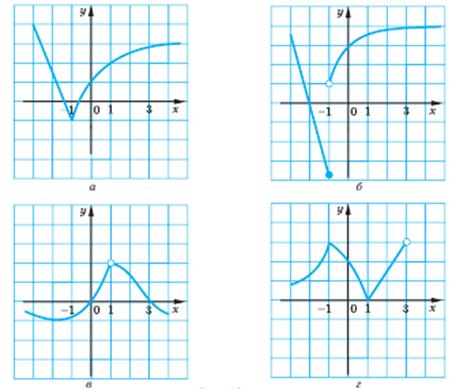 |
Рис. 1
- Чи є функція безперервною в кожній точці даного проміжку?
1) f (x) = x5 – 3x2 + 2, (-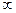 ; +
; +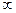 );
);
2) f (x) = , [5; +
, [5; +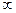 );
);
3) f (x) = , (0; +
, (0; +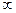 ).
).
4) f (x) = x2 – 3x, (-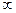 ; +
; +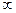 );
);
5) f (x) =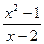 , (0; +
, (0; +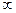 );
);
6) f (x) =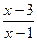 , [2; +
, [2; +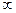 ).
).
- З'ясувати, до якого числа прагне функція f (x), якщо
1) f (x) = 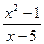 при х
при х  0;
0;
2) f (x) = x2 – 5x + 1 при х  1;
1;
3) f (x) =  при х
при х  2;
2;
4) f (x) =  при х
при х  -1;
-1;
5) f (x) = 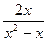 при х
при х  3.
3.
- Знайти: 1)
 (x3 + 2x - 1); 2)
(x3 + 2x - 1); 2) 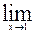
 ; 3)
; 3) 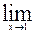
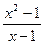 .
. - Дослідити функцію f (x) =
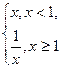 у точці х0 = 1.
у точці х0 = 1. - Дослідити функцію f (x) =
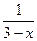 , х
, х  R, x
R, x  3 на безперервність у точці х = 3.
3 на безперервність у точці х = 3. - Дослідити функцію на безперервність у точках х = 0, х = -1, х = 1, якщо f (x) =
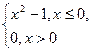
- Знайти:
1) 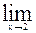 (x2 + x +5);
(x2 + x +5);
2) 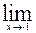 (4x –x3);
(4x –x3);
3) 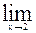 (x2 + 3x -5);
(x2 + 3x -5);
4) 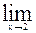
 ;
;
5) 
 ;
;
6) 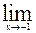
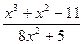 ;
;
7)  (x4 - 2x + 5);
(x4 - 2x + 5);
8) 
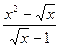 .
.
9) 
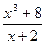 ;
;
10) 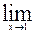
 ;
;
11) 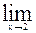
 ;
;
12) 
 ;
;
13) 
 ;
;
14) 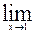
 ;
;
15) 
 ;
;
16) 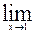
 ;
;
17) 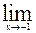
 ;
;
18) 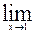
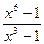 ;
;
19) 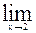
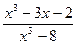 ;
;
20) 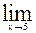
 ;
;
21) 
 ;
;
22) 
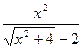 ;
;
23) 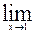
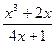 ;
;
24) 
 ;
;
25) 
 .
.
Тема. Приріст аргументу і приріст функцій. Задачі, які приводять до поняття похідної. Означення похідної, механічний та геометричний зміст
План
- Приріст аргументу і приріст функцій.
- Задачі, які приводять до поняття похідної.
- Означення похідної.
- Геометричний зміст похідної.
- Механічний зміст похідної.
- Приріст аргументу і приріст функції
| Якщо змінна величина х змінила своє значення від х0 до х1, то різниця між її новим значенням і початковим називається приростом аргументу і позначається символом ∆ х (читається: «дельта ікс»). Таким чином, ∆ х = х1 - х0, звідки випливає, що х1 = х0 + ∆ х. Кажуть також, що початкове значення аргументу х0 одержало приріст ∆ х. Внаслідок цього значення функції зміниться на величину f(х1) - f(х0). Ця різниця називається приростом функції в точці х0, відповідним до приросту ∆ х, і позначається символом ∆у (читається: «дельта ігрек») або ∆f (читається: «дельта эф»). ∆у = ∆f(x) = f(х1) - f(х0) ∆у = f(х0 + ∆ х) - f(х0). |
2. Задачі, які приводять до поняття похідної
- Миттєва швидкість руху точки вздовж прямої
| х(t) – координата х точки в момент часу t

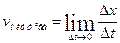
|
- Дотична до графіка функції
| Дотичною до кривої в даній точці М називається граничне положення січної MN. | |||
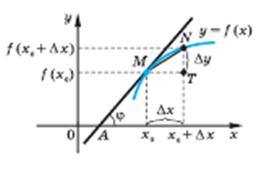
| Коли точка N наближається до точки М (рухаючись по графіку функції у = f(х)), то величина кута NМТ наближається до величини кута  нахилу дотичної МА до осі Ох.
Оскільки tg нахилу дотичної МА до осі Ох.
Оскільки tg  NМТ = NМТ =  , то
tg , то
tg  = = 
|
- Означення похідної
у = f(х)
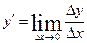

| Похідною функції у = f(х) у точці х0 називається Границя відношення приросту функції в точці х0 до приросту аргументу, коли приріст аргументу прямує до нуля. Операція знаходження похідної називається диференціюванням. |
- Геометричний зміст похідної
| Значення похідної в точці х0 дорівнює тангенсу кута нахилу дотичної до графіка функції в точці з абсцисою х0 і дорівнює кутовому коефіцієнту цієї дотичної.
(Кут відлічується від додатного напрямку осі Ох проти годинникової стрілки)
 k - кутовий коефіцієнт дотичної
k - кутовий коефіцієнт дотичної
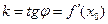
 - рівняння дотичної до графіка функції - рівняння дотичної до графіка функції 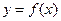 у точці з абсцисою х0 у точці з абсцисою х0
|
- Механічний зміст похідної
| Похідна характеризує швидкість зміни функції при зміні аргументу | |
| S = S (t) – залежність пройденого шляху від часу V = S ′(t) – швидкість прямолінійного руху a = v′(t) – прискорення прямолінійного руху | Зокрема, похідна за часом є мірою швидкості зміни відповідної функції, що може застосовуватися до найрізноманітніших фізичних величин. Наприклад, миттєва швидкість v нерівномірного прямолінійного руху є похідна функції, яка виражає залежність пройденого шляху s від часу t. |
- Зв'язок між диференційованістю і неперервністю функції
| Якщо функція f(х) диференційована в точці х0, то вона неперервна в цій точці. |
| Якщо функція f(х) диференційована на проміжку (тобто в кожній його точці), то вона неперервна на цьому проміжку |
План
- Похідні елементарних функцій.
- Правила диференціювання функцій.
| 1. Похідні елементарних функцій | |||
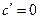
| 
| ||
 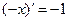
| 
| ||
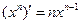
| 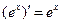
| ||
 , х , х  0 0
| 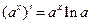 , a > 0, a - стала , a > 0, a - стала
| ||
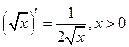
|  , ,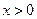
| ||
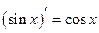
|  , ,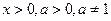 ,
a - стала ,
a - стала
| ||

|  на ОДЗ правої частини формули
на ОДЗ правої частини формули
| ||
| 2. Правила диференціювання функцій | |||
| Правило | Приклад | ||
 Сталий множник можна виносити за знак похідної
Сталий множник можна виносити за знак похідної
| 
| ||
 Похідна суми диференційованих функцій дорівнює сумі їх похідних
Похідна суми диференційованих функцій дорівнює сумі їх похідних
| 
| ||

| 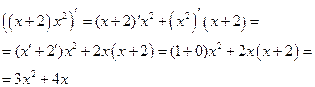
| ||
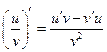
| 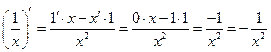
|
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 648; Нарушение авторских прав?; Мы поможем в написании вашей работы!



