
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема. Опуклість та гнучкість функції. Дослідження функції на опуклість та точку перетину
|
|
|
|
План
- Поняття другої похідної.
- Поняття опуклості і точок перетину диференційованої на інтервалі (a; b) функції.
- Властивість графіків опуклих функцій.
- Достатні умови опуклості функції, що має другу похідну на заданому інтервалі (a; b).
- Знаходження точок перегину функції, що має другу похідну на заданому інтервалі.
- Дослідження функції на опуклість і точки перегину.
| 1. Поняття другої похідної | ||||
| Поняття | Запис | Приклад | ||
Нехай функція у = f(х) має похідну f ´(х) в усіх точках деякого проміжку. Ця похідна, у свою чергу, є функцією аргументу х. Якщо функція f ´(х) є диференційованою, то її похідну називають другою похідною від f(х) і позначають 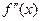 (або (або 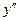 ) )
| у = f(х),
 , ,
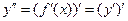 . .
| у = х5
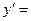 5х4 5х4
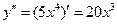
| ||
| 2. Поняття опуклості і точок перетину диференційованої на інтервалі (a; b) функції | ||||
| Функція f(х) називається опуклою вниз на інтервалі(a; b), якщо для будь - якої точки х0 із цього інтервалу при всіх х  (a; b) і (a; b) і 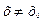 графік функції лежить вище дотичної до цього графіка в точці ( графік функції лежить вище дотичної до цього графіка в точці (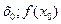 ). ).
| |||
| Функція f(х) називається опуклою вгору на інтервалі(a; b), якщо для будь - якої точки х0 із цього інтервалу при всіх х  (a; b) і (a; b) і 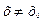 графік функції лежить нижче дотичної до цього графіка в точці ( графік функції лежить нижче дотичної до цього графіка в точці (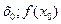 ). ).
| |||

| Точка М графіка неперервної функції f(х), у якій існує дотична і при переході через яку крива змінює напрям опуклості, називається точкою перегину графіка функції. У точці перегину графік функції переходить з одного боку дотичної до іншого. Абсцису х0 точки М перегину графіка функції f(х) називають точкою перегину функції f(х). Точка х0 розділяє інтервали опуклості функції. |
| 3. Властивість графіків опуклих функцій | ||||

| Якщо функція f(х) опукла вниз на інтервалі (a; b) і М1 та М2 - точки її графіка на цьому інтервалі, то на інтервалі (х1;х2) графік функції у = f(х) лежить нижче відрізка М1М2, тобто графік лежить нижче хорди. | |||

| Якщо функція f(х) опукла вгору на інтервалі (a; b) і М1 та М2 - точки її графіка на цьому інтервалі, то на інтервалі (х1;х2) графік функції у = f(х) лежить вище відрізка М1М2, тобто графік лежить вище хорди. | |||
| 4. Достатні умови опуклості функції, що має другу похідну на заданому інтервалі (a; b) | ||||
| Умова опуклості вниз | Умова опуклості вгору | |||
Якщо на інтервалі (a; b) двічі диференційована функція f(х) має додатну другу похідну (тобто  при всіх х при всіх х  (a; b)), то її графік на інтервалі (a; b) спрямований опуклістю вниз. (a; b)), то її графік на інтервалі (a; b) спрямований опуклістю вниз.
| Якщо на інтервалі (a; b) двічі диференційована функція f(х) має від’ємну другу похідну (тобто 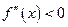 при всіх х при всіх х  (a; b)), то її графік на інтервалі (a; b) спрямований опуклістю вгору. (a; b)), то її графік на інтервалі (a; b) спрямований опуклістю вгору.
| |||
| 5. Знаходження точок перегину функції, що має другу похідну на заданому інтервалі | ||||
| Необхідна умова | Достатня умова | |||
У точках перегину функції f(х) її друга похідна дорівнює нулю або не існує.
| 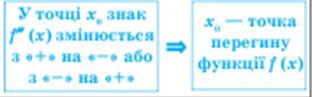 Нехай функція f(х) має на інтервалі (a; b) другу похідну. Тоді, якщо Нехай функція f(х) має на інтервалі (a; b) другу похідну. Тоді, якщо 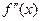 змінює знак при переході через х0, де х0 змінює знак при переході через х0, де х0  (a; b), то х0 - точка перегину функції f(х). (a; b), то х0 - точка перегину функції f(х).
| |||
| 6. Дослідження функції на опуклість і точки перегину | |
| Схема | Приклад |
| 1. Знайти область визначення функції. | Дослідіть функцію f(х) = х4 – 4х3 – 18х2 + 1 на опуклість і точки перегину.
|
| 2. Знайти другу похідну. |
2. 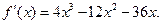

|
| 3. Знайти внутрішні точки області визначення, у яких друга похідна дорівнює нулю або не існує | 3. 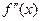 існує і неперервна на всій області визначення функції f(х). існує і неперервна на всій області визначення функції f(х). 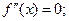 12(х2 – 2 х - 3) = 0; х1 = - 1; х2 = 3
12(х2 – 2 х - 3) = 0; х1 = - 1; х2 = 3
|
| 4. Позначити одержані точки на області визначення функції, знайти знак другої похідної і характер поведінки функції на кожному з інтервалів, на які розбивається область визначення. | 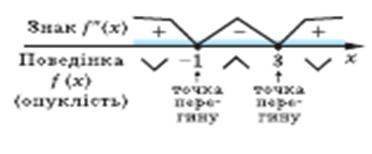
|
| 5. Записати потрібний результат дослідження (інтервали і характер опуклості і точки перегину). | На інтервалах  і і 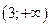 графік функції спрямовано опуклістю вниз ( графік функції спрямовано опуклістю вниз ( ), а на інтервалі ), а на інтервалі 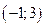 - опуклістю вгору ( - опуклістю вгору (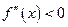 ). Точки перегину: х = -1 і х = 3 (у цих точках ). Точки перегину: х = -1 і х = 3 (у цих точках 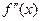 змінює знак). змінює знак).
|
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1233; Нарушение авторских прав?; Мы поможем в написании вашей работы!


